2.1 概述
1.只有两种对立逻辑状态的逻辑关系成为二值逻辑。
2.所谓逻辑，在这里是指事物间的因果关系。当两个二进制数码表示不同的逻辑状态时，它们之间可以按照指定的某种因果关系进行推理运算。我们将这种运算成为逻辑运算。
3.1849年英国数学家乔治 布尔首先提出了进行逻辑运算的数学方法布尔代数。也将布尔代数称为开关代数或逻辑代数。本章所讲的逻辑代数就是布尔代数在二值逻辑电路中的应用。
4.逻辑代数中也有字母表示变量，这种变量称为逻辑变量。
5.逻辑运算表示的是逻辑变量以及常量之间逻辑状态的推理运算，而不是数量之间的运算。
2.2逻辑代数中的三种基本运算与（AND），或（OR），非（NOT）三种
1.引入与或非概念：
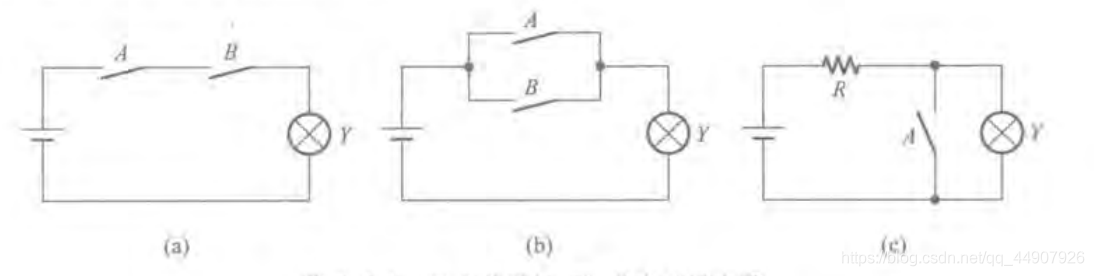如上图为三个指示灯的控制电路。
图（a）
只有当两个开关同时闭合时，指示灯才会亮。表明：只有决定事物结果的全部条件同时具备时，结果才会发生。这种因果关系成为逻辑与，或称逻辑相乘。
图（b）
只要有任何一个开关闭合，指示灯就亮。表明：在决定事物结果的诸条件中只要有任何一个满足，结果就会发生。这种因果关系称为逻辑或，也称逻辑相加。
图（c）
开关断开时灯亮，开关闭合时灯反而不亮。表明：只要条件具备了，结果便不会发生；而条件不具备时，结果一定发生。这种因果关系称为逻辑非，也称逻辑求反。
2.引入真值表：
若以A,B表示开关的状态，并以1表示开关闭合，以0表示开关断开；以Y表示指示灯的状态，并以1表示灯亮，以0表示不亮，则可以列出以0,1表示的与，或，非逻辑关系的图表。如下图。这种图表称为逻辑真值表，简称真值表。
3.引入运算符号以及图形符号
（1）运算符号：
在逻辑代数中，将与，或，非看做是逻辑变量A,B间的三种最基本的逻辑运算。
A和B进行与逻辑运算时可写成：
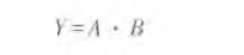
A和B进行或逻辑运算时可写成：
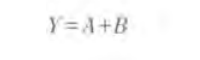
对A进行非逻辑运算时可写成：
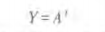
同时，将实现与逻辑运算的单元电路称为与门；
将实现或逻辑运算的单元电路称为或门；
将实现非逻辑运算的单元电路称为非门（也称为反相器）。
（2）图形符号：
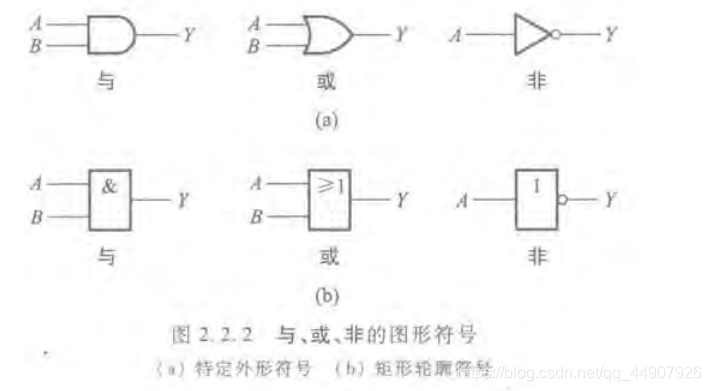用特定外形符号这套的比较多，咱也就用这个了。个人感觉还好记还好看！
4.进阶版：看看复合逻辑运算：
实际的逻辑问题往往比与，或，非复杂的多，不过他们都可以用于，或，非的组合来实现。
（1）与非（NAND）
定义：将A,B先进行与运算，然后将结果求反，最后得到的即为A，B的与非运算结果。
1.真值表：
2.图形符号及运算符号：
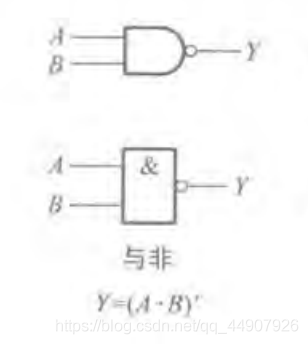
（2）或非（NOR）
定义：将A，B先进行或运算，然后将结果求反，最后得到的即为A，B的或非运算结果。
1.真值表：
2.图形符号及运算符号：
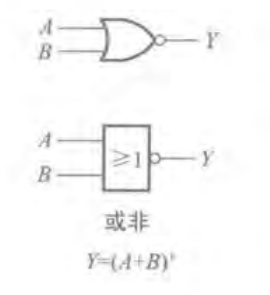
（3）与或非（AND-NOR）
定义：在与或非逻辑中，A,B之间以及C,D之间都是与的关系，只要A,B或C,D任何一组同时为1，输出Y就是0；只有当每一组输入都不全是1时，输出Y才是1。
1.真值表：
2.运算符号及图形符号：
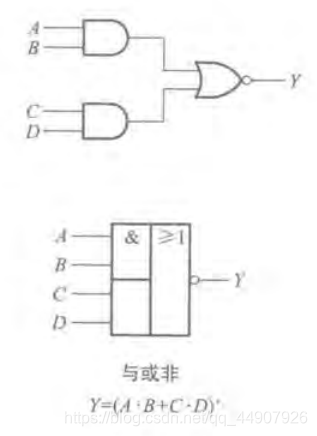
（4）异或（EXCLUSIVE OR）
定义：当A，B不同时，输出Y为1；而当A，B相同时，输出Y为0。也可以用与，或，非的组合表示：
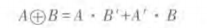
#####1.真值表：
2.图形符号及运算符号：
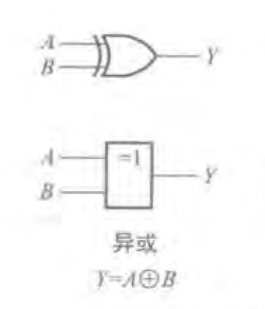
（5）同或（EXCLUSIVE NOR）
定义：同或和异或相反，当A,B相同时，Y等于1；当A,B不同时，Y等于0.同或也可以写成与，或，非的组合形式：
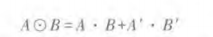
#####1.真值表：
2.图形符号及运算符号：
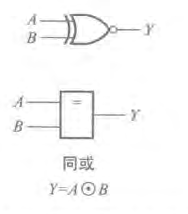
小知识点：
异或和同或互为反运算，即：
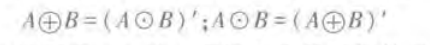
2.3逻辑代数的基本公式和常用公式
1.基本公式：
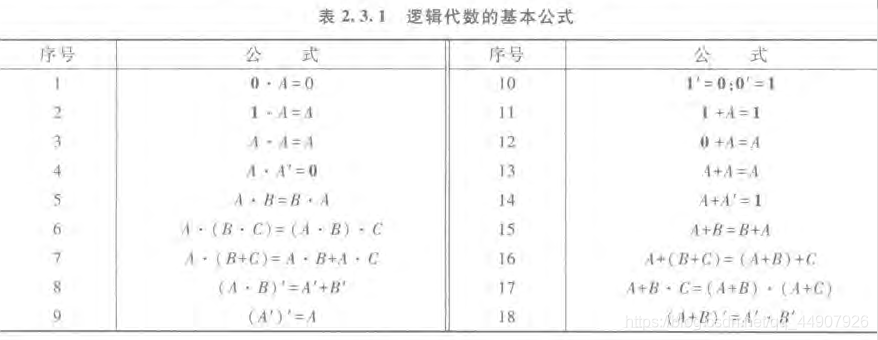
（1）式1，2,11和12给出了变量与常量间的运算规则。
（2）式3和13是同一变量的运算规律，也称为重叠律。
（3）式4和14表示变量与它的反变量之间的运算规律，也称为互补律。
（4）式5和15为交换律； 式6和16为结合律；式7和17为分配律。
（5）式8和18是著名的德摩根定理，亦称反演律。在逻辑函数的化简和交换中经常要用到这一对公式。
（6）式9表明，一个变量经过两次求反运算之后还原为其本身，所以该式称为还原律。
（7）式10是对0和1求反运算的规则，它表明0和1互为求反的结果。
小知识点：
1.公式的正确性可以使用列真值表的方法加以验证。如果等式成立，那么将任何一组变量的取值带入公式两边所得的结果应该相等。因此，等式两边所对应的真值表也必然相同。
2.仔细观察可知：公式1和11；2和12；3和13；4和14；5和15；6和16；7和17；8和18皆为对偶式。因此，只要证明公式1到8成立，则公式11到18已无需另做证明了。
2.若干常用公式：（这些公式是利用基本公式导出的！）
（1）式21的证明：
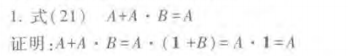
上式说明：在两个乘积项相加时，若其中一项以另一项为因子，则该项是多余的，可以删去。
（2）式22的证明：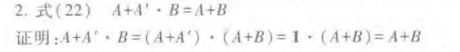
上式表明：两个乘积项相加时，如果一项取反后是另一项的因子，则此因子是多余的，可以消去。
（3）式23的证明：
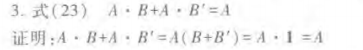
上式表明：当两个乘积项相加时，若它们分别包含B和B’两个因子而其他因子相同，则两项定能合并，且可将B和B’两个因子消去。
（4）式24的证明：
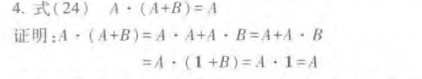
上式表明：变量A和包含A的和相乘时，其结果等于A，即可以将和消掉。
（5）式25的证明;
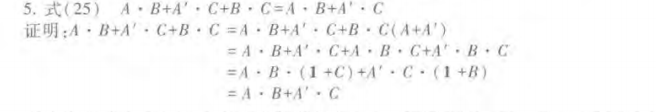
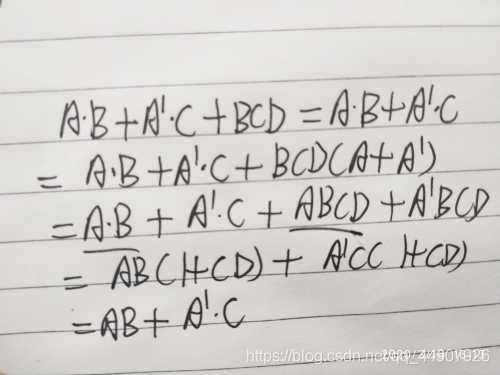上式表明：若两个乘积项中分别包含A和A’两个因子，而这两个乘积项的其余因子组成第三个乘积项时，则第三个乘积项是多余的，可以消去。
（6）式26的证明：
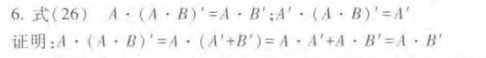
上式说明：当A和一个乘积项的非相乘，且A为乘积项的因子时，则A这个因子可以消去。
上式表明：当A‘和一个乘积项的非相乘，且A为乘积项的因子时，其结果就等于A’。
2.4逻辑代数的基本定理
1.代入定理
代入定理：在任何一个包含变量A的逻辑等式中，若以另外一个逻辑式代入式中所有A的位置，则等式仍然成立。
（1）理解：
因为变量A仅有0和1两种可能的状态，所有无论将A=0还是A=1代入逻辑等式，等式都一定成立。而任何一个逻辑式的取值也不外0和1两种，所以用它取代式中的A时，等式自然也成立。所以，可以将此定理看成无需证明的公理。
（2）例子：（以德摩根定理为例）
小知识点：
对一个乘积项或逻辑式求反时，应在乘积项或逻辑式外边加括号，然后对括号内的整个内容求反。
此外，在对复杂的逻辑式进行运算时，仍需遵守与普通代数一样的运算优先顺序，即先算括号里的内容，其次算乘法，最后算加法。
2.反演定理
例1：
例2：
3.对偶定理
注意：和反演定理的区别是：反演定理还有原变量变为反变量，反变量变为原变量！！！
例子：
