数字电路的作用是用来表达一个现实的逻辑命题,实现逻辑功能。但是,从
逻辑功能中简单概括得出的逻辑函数,往往不是最简表达式,根据这样的非最简式来实现电路,系统会过于复杂,成本过高,同时,电路运行的安全性和可靠性也无法得到保障。
为了降低系统成本,提高工作可靠性,应在不改变逻辑功能的基础上,化简
逻辑表达式,降低其规模,并进行相应变形,用更合理的函数式表达逻辑命题,以期用最少、最合理的门电路器件实现逻辑功能。
逻辑函数的化简原则:
- 逻辑电路所用的门最少
- 每个门的输入端要少
- 逻辑电路所用的级数要少
- 逻辑电路能可靠地工作
逻辑函数的化简:
逻辑函数的表示工具:
- 真值表
- 逻辑表达式
- 卡诺图
- 逻辑电路图
- 波形图
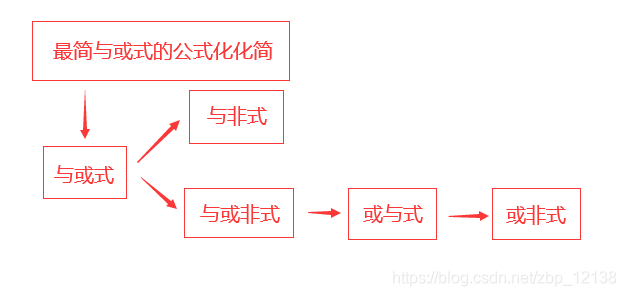
公式化简法
与或逻辑函数的公式法化简
 公式化化简思路:
公式化化简思路:
- 有直接利用化简公式的结构,就直接化简
- 若没有,就改变表达式结构,创造环境去化简(拆项、提取公因子)
特殊技巧:
- 反用多余项定律
- 加0因子
另外,化简结果可能不唯一,但最后结果的长度都是一样的
5类逻辑函数之间的转换

方法结构图如下所示:
卡诺图化简法
卡诺图的由来和原理
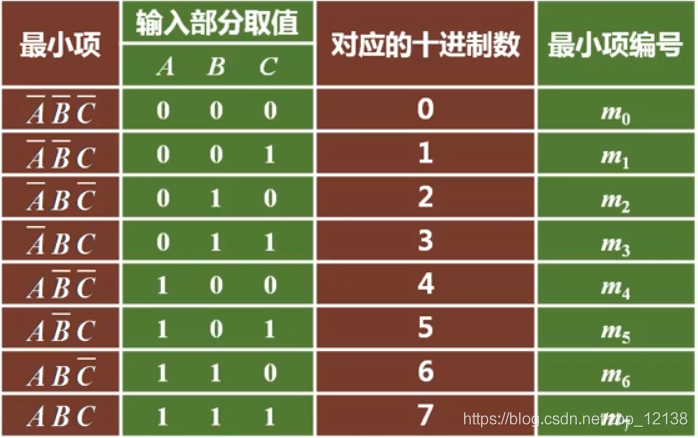
对于一个给定了变量数目的逻辑函数,所有变量都参加相“与”的与项称为最小项,下面的ABC、AB 、 BC、 C都是最小项:
F = f(A,B,C) = AB +
C = AB(C+
) +
C(B+
)
= ABC + AB
+
BC +
C
最简与或表达式拆项后得到的表达式的每个与项中,三输入变量均以原变量或者反变量形式,出现且仅出现一次。所以说,这 4 个与项都是该逻辑函数的最小项。
- 最小项的特点:
每个与项均包含了该逻辑函数的所有变量,且每个变量只能
以原变量或反变量形式出现且仅出现一次。
由此可知:
- 1 变量逻辑函数 有 2 个最小项:
A、 - 2 变量逻辑函数 有 4 个最小项:
AB、 B、A 、 - 3 变量逻辑函数 有 8 个最小项:
ABC、 BC、A C、AB 、 C、A 、 B 、
n变量逻辑函数共有2”个最小项
所谓“标准与或式”,就是用最小项相加 , 得到的与或表达式,也称为最
小项标准式、“最小项之和”形式
一个具体逻辑函数的标准与或式中,到底存在哪个最小项,要看表达
式的具体情况
标准与或式和真值表的联系
逻辑函数F = AB +
C的真值表:
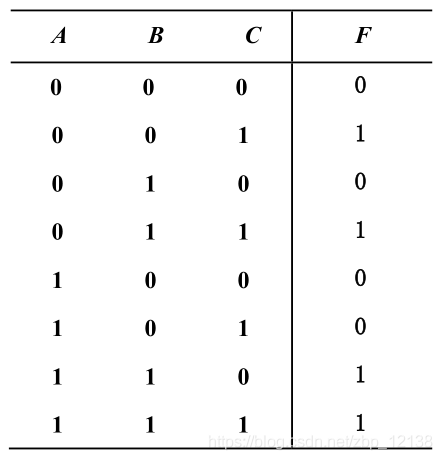
由真值表可知,该逻辑函数共有 4 种输入组合,能使输出成立:
001、011、110、111
该逻辑函数的最简与或式和标准与或式分别为:
F = AB +
C
= ABC + AB
+
BC +
C
F 的标准与或式由 4 个最小项组成,用 0 表示反变量,1 表示原变量,则能使输出成立的 4 种输入组合,恰好和 4 个最小项一一对应。也就是说, 一个最小项就 对应着真值表上的 一行, 对应着一组确定的输入条件组合。
真值表上,有 4 种输入组合能使输出为 1,就将这 4 种输入组合所对应的 4
个最小项相或,从而得到逻辑函数的标准与或式。由此可知, 逻辑函数的真值表和标准与或式是严格对应的,都准确地表达了一个逻辑命题的功能 , 这就是最小项、标准与或式的逻辑含义。
综上所述:
- 标准与或式具有唯一性,和该逻辑函数的真值表严格对应 ,代表了逻辑函数的功能 ;
- 一般式则具有多样性,代表了实现逻辑函数 的电形式的多样性。
最小项的基本性质
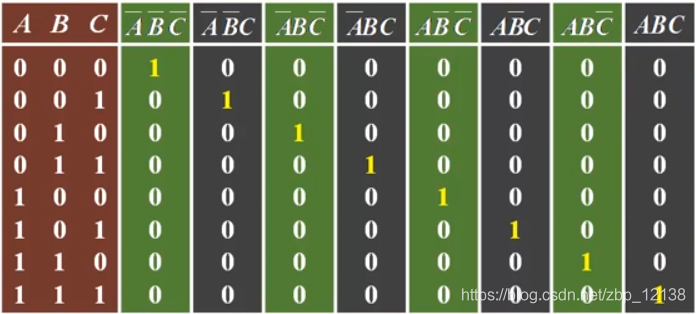
- 在输入的任一种取值下,有且仅有一个最小项的值为1
- 一个逻辑函数的任意两个最小项之积必为0
- 一个逻辑函数的全体最小项之和必为1
最小项的编号
卡诺图的结构规则
卡诺图上的一个方格就对应着逻辑函数的一个最小项

- 同一个逻辑函数,真值表的输出部分有几个1 ,卡诺图方格内就要填几个1 ,都表示了有几个输入组合能够使输出成立;
- 逻辑函数的输入变量个数确定了真值表的结构、卡诺图的结构。
卡诺图的化简原理
拿四输入卡诺图举例:
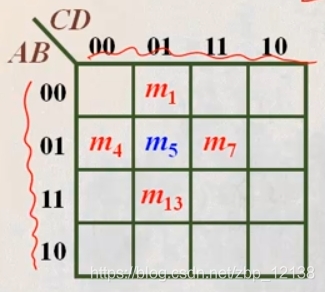
注意列写顺序: 00,01,11,10
B D = m5
在一个最小项标准中,所有跟这一与项逻辑相邻的,只有四种可能:
- D = m1
- B = m4
- BCD = m7
- AB D = m13
逻辑相邻的意思,就意味着四输入变量中,两个与项相对应,只有一个变量,原变量、反变量不同,剩余三个变量是相同的
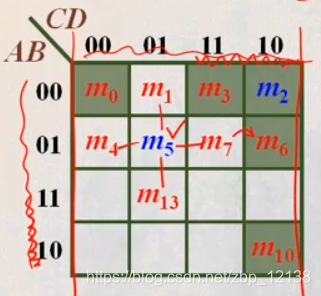
如果将以上五项标在图上:
类似的:
C
= m2
跟这一与项逻辑相邻的:
- = m0
- CD = m3
- BC = m6
- A C = m10
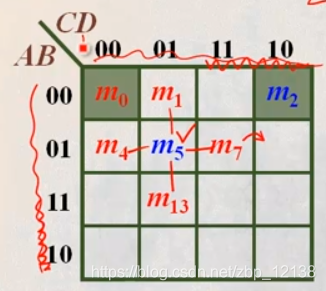
m0与m2是相邻的,所以整个卡诺图是左右相通的,就想个滚筒一样:
 而一个五输入的卡诺图却是左右对称的:
而一个五输入的卡诺图却是左右对称的:
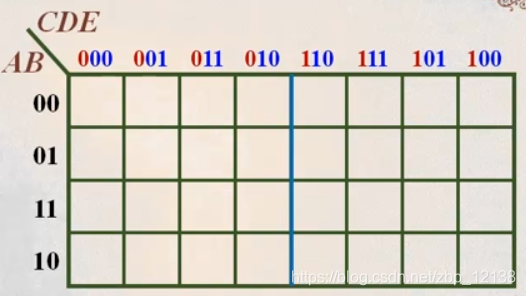
跟某一项逻辑相邻的,有5种可能:
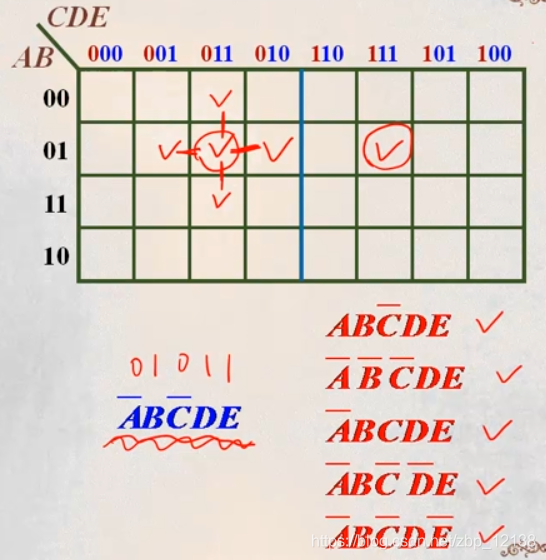
卡诺图能帮助我们更好地寻找逻辑相邻关系,但是到了五输入时,这一规则被打破了。也就是说,五变量以上的卡诺图就没有太多的使用意义
与或逻辑函数的卡诺图法化简
最小项合并规则
在卡诺图中,凡是相邻的最小项,它们在逻辑上也是相邻的,逻辑相邻,就是指二个最小项中除一个变量的形式不同为互反变量外,其它都是相同的,因此它们可以合并成一个与项,消去其中互反变量
两个相邻项的合并

首先先把相邻项圈起来,这个圈叫卡诺圈:
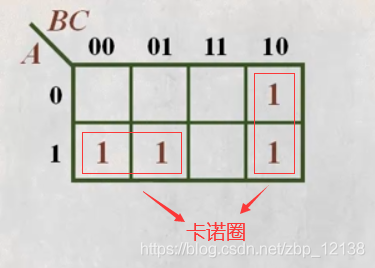
每一个卡诺圈表示可以进行一次 吸收定理1:
二个最小项合并,消去一个互反变量,保留公共变量(两项变一项,谁变干掉谁)
对于上面的两个圈:
- A + A C = A
- B + AB = B
再来看看下面这张卡诺图:
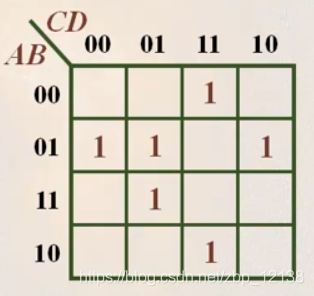 画出卡诺圈:
画出卡诺圈:
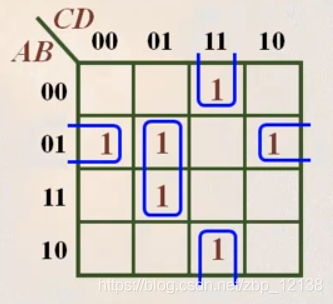
对这三个圈进行化简:
- B D + AB D = B D
- CD + A CD = CD
- B + BC = B
四个相邻项的合并
刚刚的两个相邻项可以消去1个变量,这里的四个相邻项可以消去2个变量
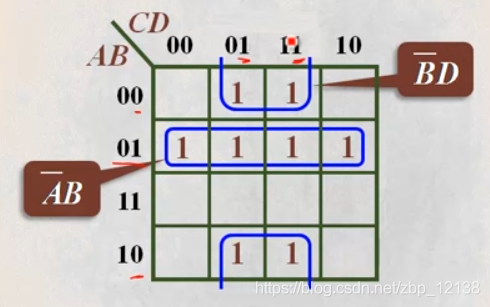

八个相邻项的合并
有了上面的基础,这里应该就可以知道,八个相邻项可以消3个变量

换句话说就是: 谁不变,就把谁留下
奇葩相邻项
看一下这两个圈:

注意!这样画圈是无法化简的!!!
应该转换成2个两项圈和2个四项圈:
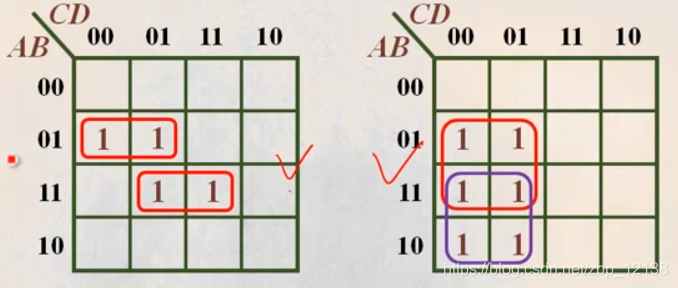
总结:
- 2”个相邻最小项组成的卡诺圈合并,可以消去n个变量
- 不存在包含非2"个最小项的卡诺圈
- 看坐标化简,多项变一项,保留不变的,消去变化的。
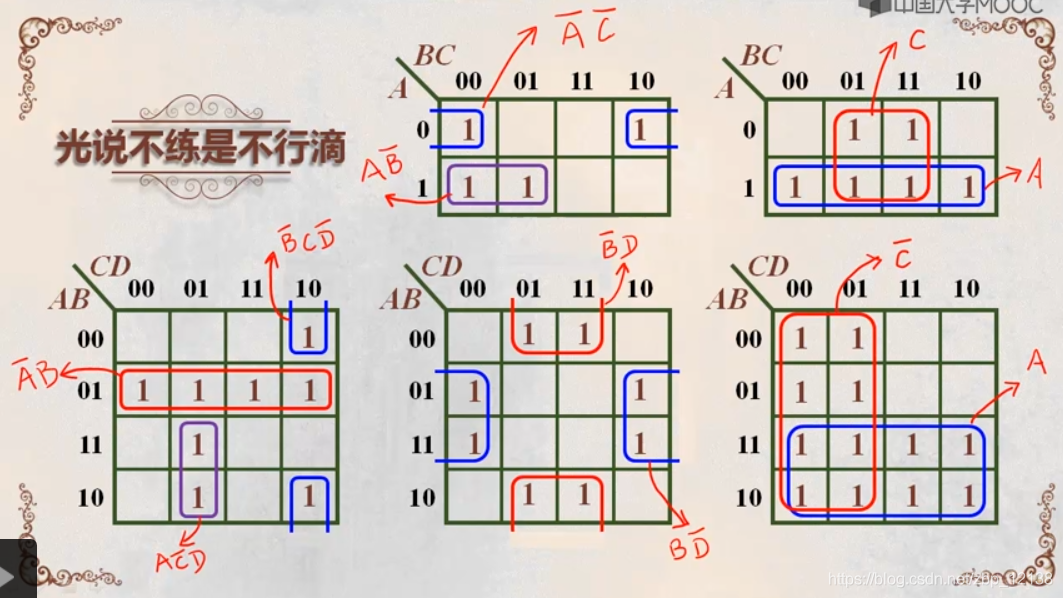
用卡诺图表达待化简的逻辑函数
步骤:
- 根据表达式中输入变量个数, 画出卡诺图的结构
- 表达式中包含什么样的最小项,在卡诺图对应的方格上填1 ,其余的填0或者不填,就得到了完整的卡诺图
三种典型情况:
- 与或表达式
- 标准与或式(最小项标准式、最小项之和)
- 其他任何一般表达式
与或表达式
[例] F = B + AC
确定为四输入卡诺图:
坐标1表示原变量、0表示反变量,按坐标规定,将与或式中的各个与项逐一填入卡诺图
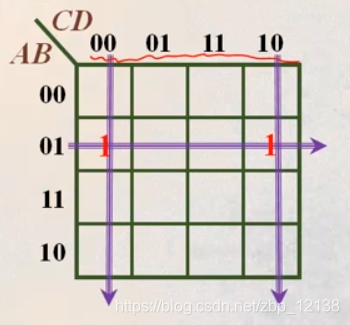
先看第一项
B
,拆项后即
B
(C+
):
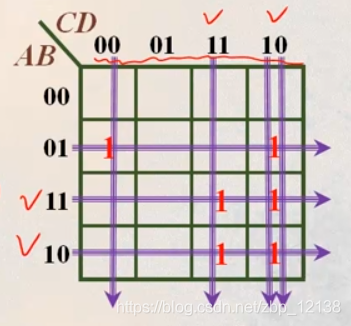
再来看看第二项AC经过拆项后AC(B+
)(D+
):
标准与或式
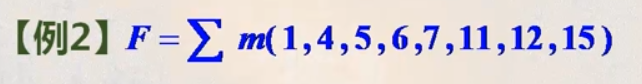 即 F = m1 + m4 + m5 + … + m15
即 F = m1 + m4 + m5 + … + m15
最小项标准式中,最小项编号最大是15 ,说明是四输入逻辑函数,由此得到卡诺图的结构:
根据最小项的排列规律填入最小项:
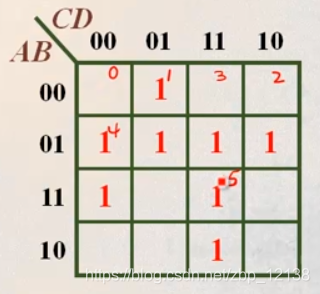
其他一般表达式
 有了上面的基础,这里很容易就能判断出是四输入:
有了上面的基础,这里很容易就能判断出是四输入:
变形后得到与或式:

填入卡诺图:
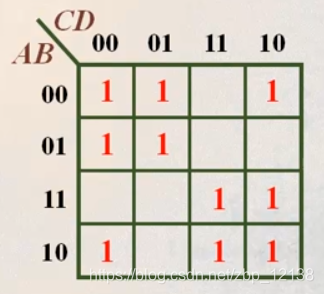

再来看下一道例题:
 这道题也再次证明了化简结果是不唯一的,但化简得长度是唯一的
这道题也再次证明了化简结果是不唯一的,但化简得长度是唯一的
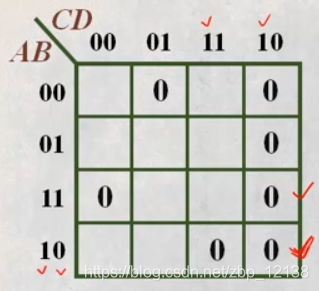
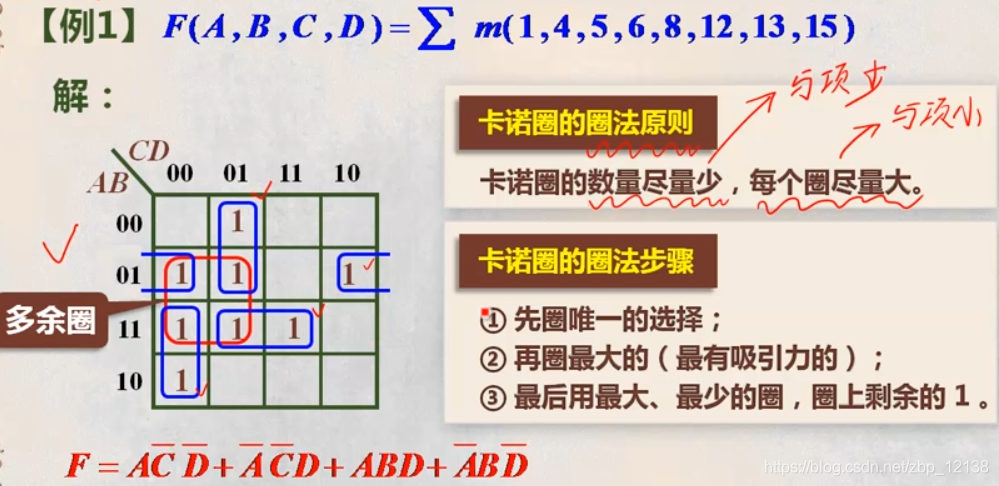 对于下面这一题,我们可以找出 F=0的情况,再填入1:
对于下面这一题,我们可以找出 F=0的情况,再填入1:

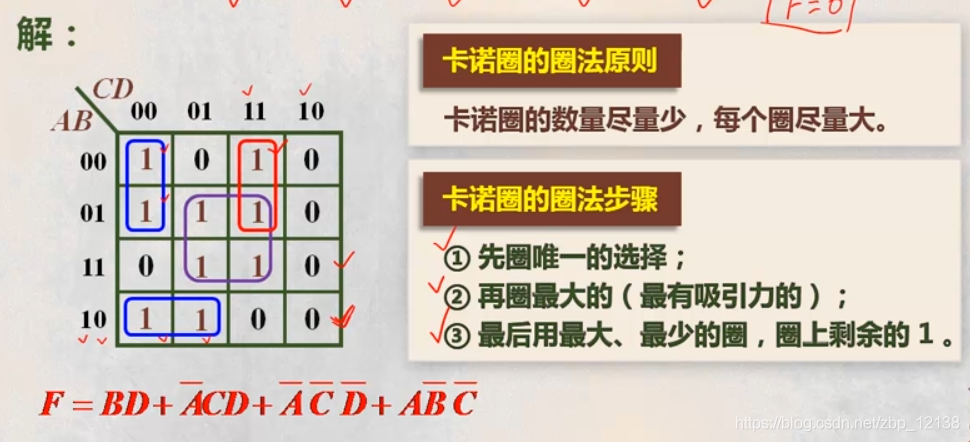
最终结果如下:
5类逻辑函数的卡诺图法化简

- 其实真正用到卡诺图法的是:
与或式、或与式以及与或非式
与非-与非式
- 用卡诺图表达出待化简函数,圈“1”得到最简与或式
- 与或式两次求反,摩根定律展开一层,得到最简与非-与非式。
[例] F = D + D + BC + A D
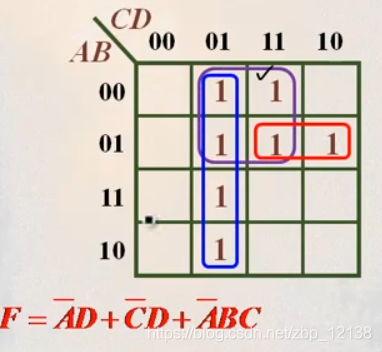
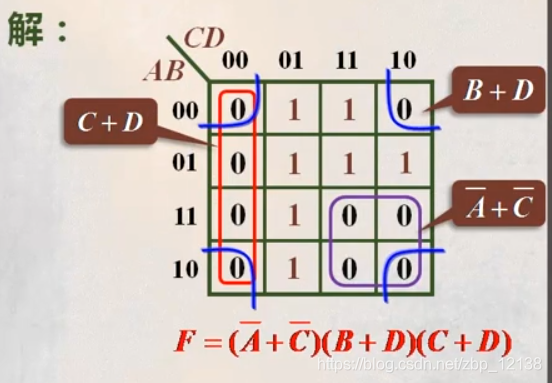
或与式
- 用卡诺图表达出待化简逻辑函数
- 图上圈0, 并且,坐标0表示原变量 ,1表示反变量,变量相“或”得到每一个或项(反演定律)
- 最后再将所有的或项相“与",得到最简或与式
[例] F = D + D + BC + A D
再来看另一题:
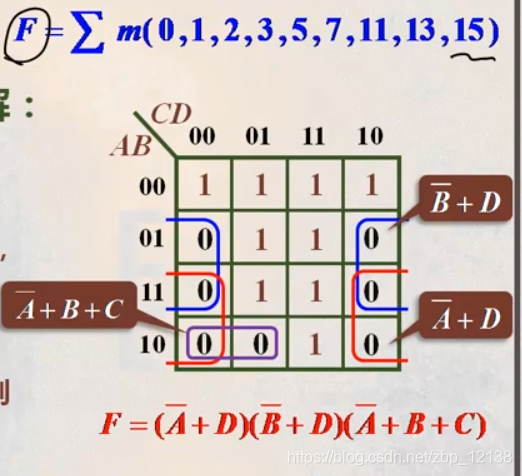
或非-或非式
已知最简或与式,两次求反,再摩根定律展开一层,得到最简或非-或非式。
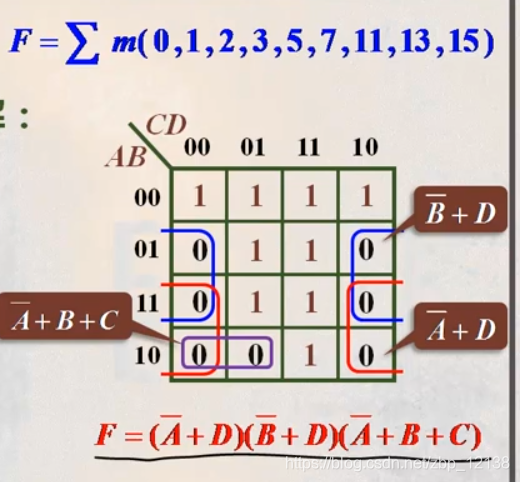 利用公式化两次取反:
利用公式化两次取反:
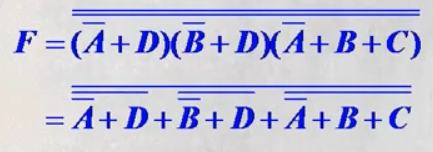
与或非式
- 在卡诺图上圈"0”,求出反函数的最简与或式;
- 然后取反,不处理,就得到最简与或非式。
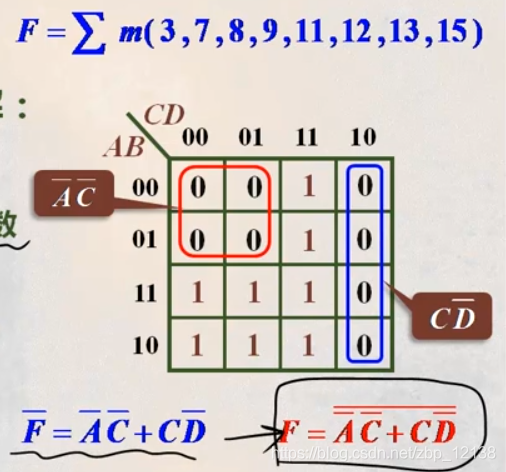
完整总结

具有约束关系的逻辑函数
-
约束关系:
输入变量的取值不是任意的,而是有条件的,并不是所有的输入组合都可以出现 -
具有约束的变量:
在实际应用中,某些现实条件限制了输入变量的取值,将具有限制关系的一组输入变量称为一组具有约束的变量 -
具有约束的逻辑函数:
由具有约束关系的输入变量所决定的逻辑函数,就称为具有约束的逻辑函数 -
完全描述问题:
n输入的逻辑函数的2的n次方种输入取值组合下的输出取值都是明确的,这样的逻辑函数就是完全描述问题,其功能与每一个最小项均有关 -
非完全描述问题:
具有约束的逻辑函数就是非完全描述问题,其功能只与能够出现的最小项有关 -
约束项:
不可能出现的最小项,自然谈不上输出是0还是1 -
任意项:
某些最小项出现时输出是1还是0均可,不影响逻辑电路的功能 -
无关项:
约束项和任意项统称为无关项,逻辑函数的功能都跟他们无关
但并不是所有无关项都适合加入,有的无关项加入表达式后,反而会使表达式变得复杂。
总结:
- 具有约束关系时,首选卡诺图法化简,保证最简原则
- 化简结果中要同时写上约束条件
- 最好将约束条件也做相应化简
例如,设计一个现实的逻辑电路,用一个指示灯来表示一架电梯的运行状态,从而能估计电梯日常使用频率。设计要求:当电梯在上升和下降时,指示灯点亮,表示电梯正在响应用户的使用要求;而当电梯悬停在某一层时,指示灯灭,表示电梯空闲。
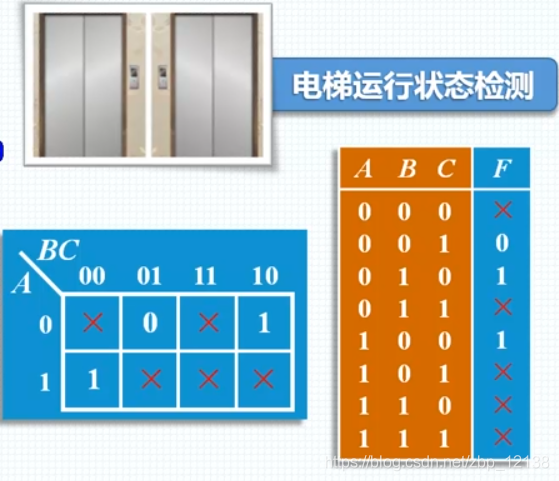
不难发现:这是三条件、一结论的逻辑命题,设输入变量为 A 、 B 、 C ,分别表示电梯处于“上升”、“下降”和“悬停”,输出变量为 F ,表示指示灯点亮。在这个逻辑函数的八种输入取值组合中,能够使输出为 1 的组合只有两个,因此可以简单得到逻辑表达式:
- F = A + B
同时,因为一些现实因素的限制,输入变量的某些取值组合永远不可能出现
电梯是不可能同时一边上升、一边下降的,也不可能一边上升、一边停止,
同样,也不可能既不上升、又不下降。也不停止。
以此类推,逻辑函数有五种输入组合是永远不可能出现,自然谈不上在这些输入组合下,输出取值为:
- = m0
- BC = m3
- A C = m5
- AB = m6
- ABC = m7
这就是该命题所包含的约束关系
此外,理论上还有一种情况,就是在输入变量的某些最小项出现(即对应的
输入组合出现)时,输出函数值是 1 还是 0 均可,不影响逻辑电路的功能,这样的最小项称为任意项
- 如果是约束项,则意味着不可能出现的最小项,那么谈不上输出是1 还是0
- 如果是任意项,则输出无所谓 1 还是 0
不论是约束项还是任意项,逻辑函数的功能都跟它们无关,因此, 约束项和任意项统称为无关项
既然约束项和任意项最终对输出造成的影响是类似的,一般不对它们做过于
绝对的区分,具有这种特点的逻辑函数统称为 具有无关项的逻辑函数,或者称为具有约束关系的逻辑函数,两者是一个概念
约束关系的理解和表述
-
约束关系的表述:
约束表达式限制了什么样的输入组合出现,把它们总结起来,就是约束关系的语言表达。 -
约束关系的数学化:
将一个现实的逻辑约束所限制的输入组合用表达式总结出来。
= 0
B、C不能同时为0
BC = 0:
B、C不能同时为1
= 1:
B、C取值必为00
B、C中不能有1
B + C = 1:
B、C不能同时为0
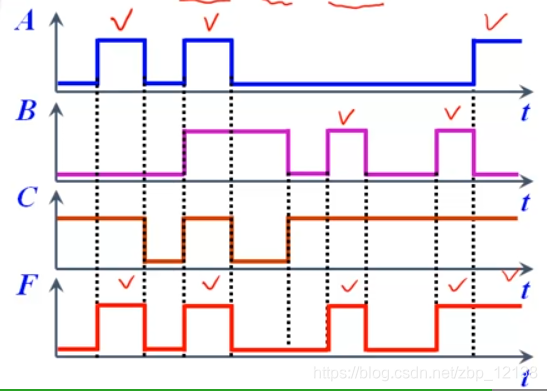
波形图
以时间为横轴,画出一个逻辑函数的输入、输出变量对应变化的波形,从而形成输入信号和输出信号的对应图形,即逻辑电路的波形图
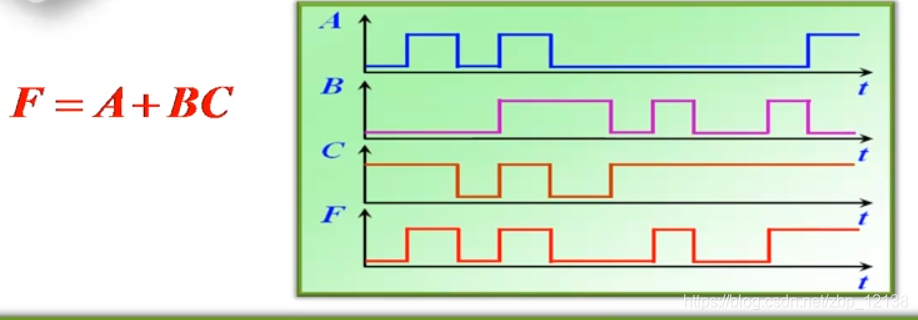
波形图的整体分析法
1.将3个输入波形的所有变化点标记出来,这也就是输出波形可能的变化点。
2.以整体分析的方式画输出波形(似于真值表的列写过程,切忌从头到属地逐个片段画)
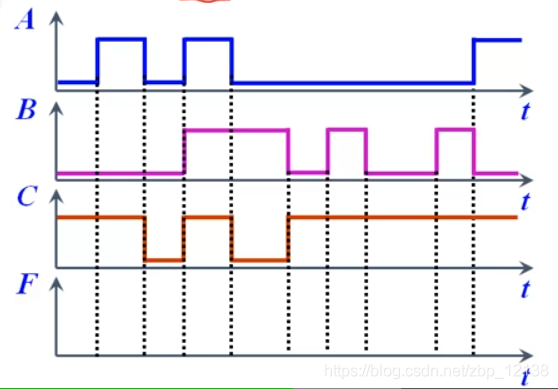
找出A和BC分别为1时的对应段,那么剩下的都是0:
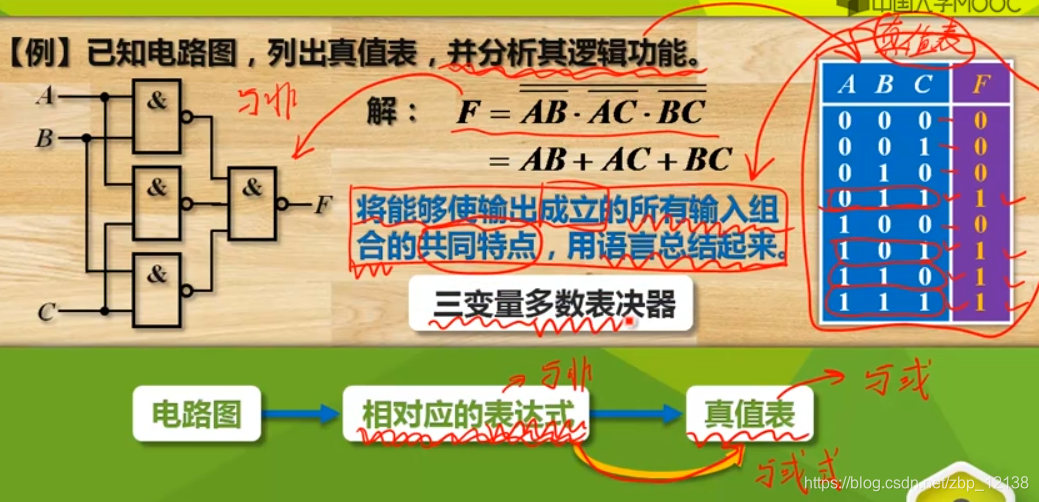
组合逻辑电路分析和设计基础
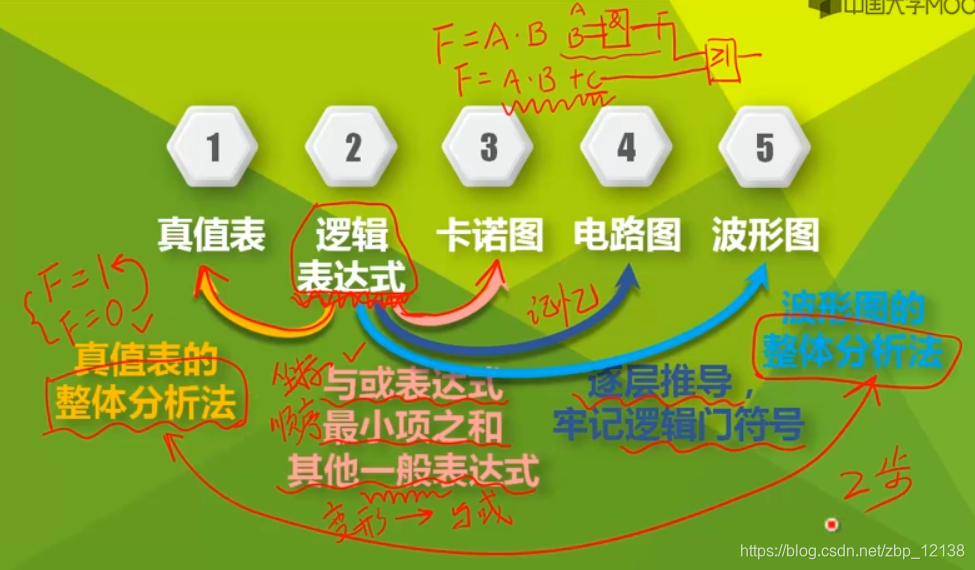
五个逻辑函数的表示工具
- 真值表
- 逻辑表达式
- 卡诺图
- 逻辑电路图
- 波形图
各种表示工具的相互转化
由逻辑表达式转换为其他工具
其他工具转化为逻辑表达式

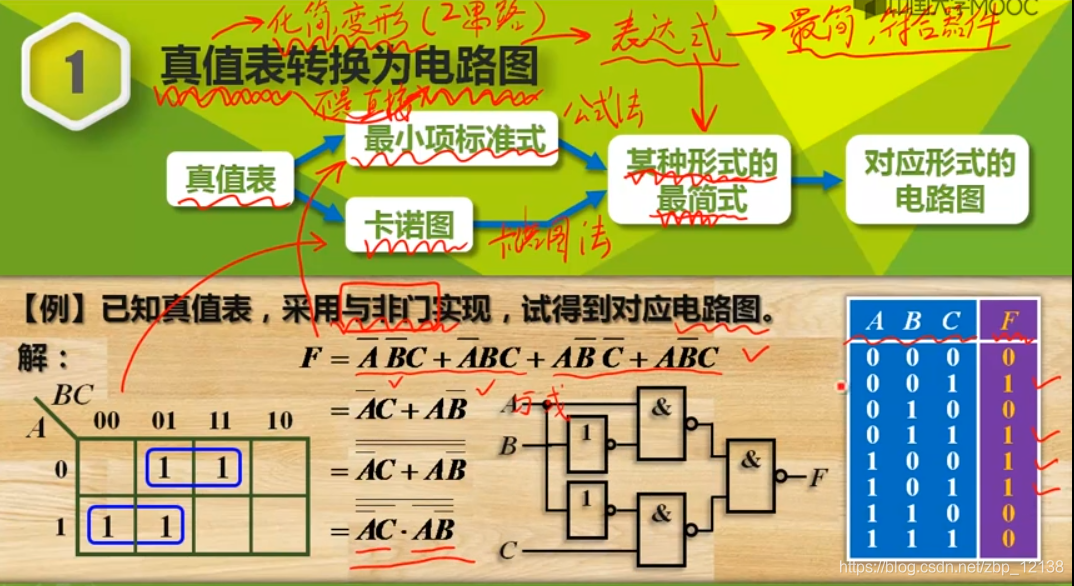
真值表转化为电路图
电路图转化为真值表