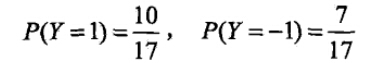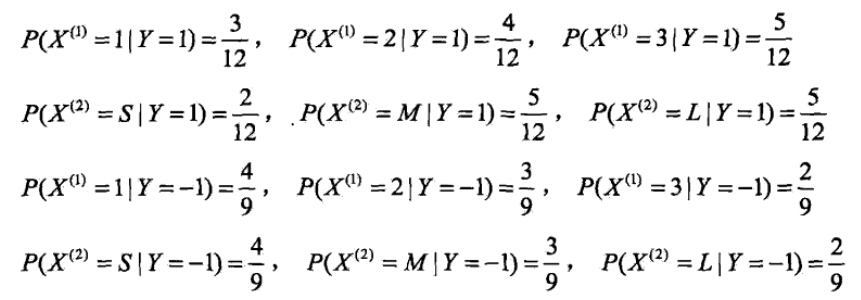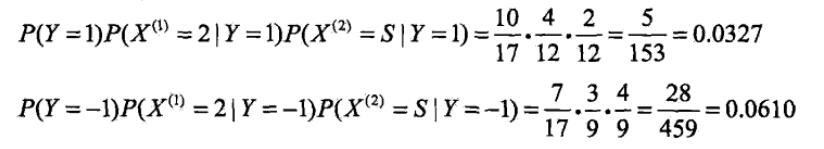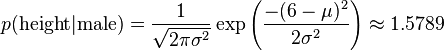在文本分类中,假设我们有一个文档d∈X,X是文档向量空间(document space),和一个固定的类集合C={c1,c2,…,cj},类别又称为标签。显然,文档向量空间是一个高维度空间。我们把一堆打了标签的文档集合<d,c>作为训练样本,<d,c>∈X×C。例如:
<d,c>={Beijing joins the World Trade Organization, China}
对于这个只有一句话的文档,我们把它归类到 China,即打上china标签。
我们期望用某种训练算法,训练出一个函数γ,能够将文档映射到某一个类别:
γ:X→C
这种类型的学习方法叫做有监督学习,因为事先有一个监督者(我们事先给出了一堆打好标签的文档)像个老师一样监督着整个学习过程。
朴素贝叶斯分类器是一种有监督学习,常见有两种模型,多项式模型(multinomial model)和伯努利模型(Bernoulli model)。
1.多项式模型
在多项式模型中, 设某文档d=(t1,t2,…,tk),tk是该文档中出现过的单词,允许重复,则
先验概率P(c)= 类c下单词总数/整个训练样本的单词总数
类条件概率P(tk|c)=(类c下单词tk在各个文档中出现过的次数之和+1)/(类c下单词总数+|V|)
V是训练样本的单词表(即抽取单词,单词出现多次,只算一个),|V|则表示训练样本包含多少种单词。在这里,m=|V|, p=1/|V|。
P(tk|c)可以看作是单词tk在证明d属于类c上提供了多大的证据,而P(c)则可以认为是类别c在整体上占多大比例(有多大可能性)。
给定一组分类好了的文本训练数据,如下:
docId |
doc |
类别 In c=China? |
1 |
Chinese Beijing Chinese |
yes |
2 |
Chinese Chinese Shanghai |
yes |
3 |
Chinese Macao |
yes |
4 |
Tokyo Japan Chinese |
no |
给定一个新样本Chinese Chinese Chinese Tokyo Japan,对其进行分类。
该文本用属性向量表示为d=(Chinese, Chinese, Chinese, Tokyo, Japan),类别集合为Y={yes, no}。
类yes下总共有8个单词,类no下总共有3个单词,训练样本单词总数为11,因此P(yes)=8/11, P(no)=3/11。类条件概率计算如下:
P(Chinese | yes)=(5+1)/(8+6)=6/14=3/7 //类yes下单词Chinese在各个文档中出现过的次数之和+1/类yes下单词的总数(8)+总训练样本的不重复单词(6)
P(Japan | yes)=P(Tokyo | yes)= (0+1)/(8+6)=1/14
P(Chinese|no)=(1+1)/(3+6)=2/9
P(Japan|no)=P(Tokyo| no) =(1+1)/(3+6)=2/9
分母中的8,是指yes类别下textc的长度,也即训练样本的单词总数,6是指训练样本有Chinese,Beijing,Shanghai, Macao, Tokyo, Japan 共6个单词,3是指no类下共有3个单词。
有了以上类条件概率,开始计算后验概率,
P(yes | d)=(3/7)3×1/14×1/14×8/11=108/184877≈0.00029209 //Chinese Chinese Chinese Tokyo Japan
P(no | d)= (2/9)3×2/9×2/9×3/11=32/216513≈0.00014780
因此,这个文档属于类别china。
2.伯努利模型
P(c)= 类c下文件总数/整个训练样本的文件总数
P(tk|c)=(类c下包含单词tk的文件数+1)/(类c的文档总数+2)
在这里,m=2, p=1/2。
还是使用前面例子中的数据。
类yes下总共有3个文件,类no下有1个文件,训练样本文件总数4,因此P(yes)=3/4, P(Chinese | yes)=(3+1)/(3+2)=4/5
P(Japan | yes)=P(Tokyo | yes)=(0+1)/(3+2)=1/5
P(Beijing | yes)= P(Macao|yes)= P(Shanghai |yes)=(1+1)/(3+2)=2/5
P(Chinese|no)=(1+1)/(1+2)=2/3
P(Japan|no)=P(Tokyo| no) =(1+1)/(1+2)=2/3
P(Beijing| no)= P(Macao| no)= P(Shanghai | no)=(0+1)/(1+2)=1/3
有了以上类条件概率,开始计算后验概率,
P(yes | d)=P(yes)×P(Chinese|yes) ×P(Japan|yes) ×P(Tokyo|yes)×(1-P(Beijing|yes)) ×(1-P(Shanghai|yes))×(1-P(Macao|yes))
=3/4×4/5×1/5×1/5×(1-2/5) ×(1-2/5)×(1-2/5)=81/15625≈0.005
P(no | d)= 1/4×2/3×2/3×2/3×(1-1/3)×(1-1/3)×(1-1/3)=16/729≈0.022
因此,这个文档不属于类别china。
3.两个模型的区别
二者的计算粒度不一样,多项式模型以单词为粒度,伯努利模型以文件为粒度,因此二者的先验概率和类条件概率的计算方法都不同。
计算后验概率时,对于一个文档d,多项式模型中,只有在d中出现过的单词,才会参与后验概率计算,伯努利模型中,没有在d中出现,但是在全局单词表中出现的单词,也会参与计算,不过是作为“反方”参与的。
朴素贝叶斯是一个很不错的分类器,在使用朴素贝叶斯分类器划分邮件有关于朴素贝叶斯的简单介绍。
若一个样本有n个特征,分别用表示,将其划分到类的可能性为:
上式中等号右侧的各个值可以通过训练得到。根据上面的公式可以求的某个数据属于各个分类的可能性(这些可能性之和不一定是1),该数据应该属于具有最大可能性的分类中。
一般来说,如果一个样本没有特征,那么将不参与计算。不过下面的伯努利模型除外。
以上是朴素贝叶斯的最基本的内容。
高斯模型
有些特征可能是连续型变量,比如说人的身高,物体的长度,这些特征可以转换成离散型的值,比如如果身高在160cm以下,特征值为1;在160cm和170cm之间,特征值为2;在170cm之上,特征值为3。也可以这样转换,将身高转换为3个特征,分别是f1、f2、f3,如果身高是160cm以下,这三个特征的值分别是1、0、0,若身高在170cm之上,这三个特征的值分别是0、0、1。不过这些方式都不够细腻,高斯模型可以解决这个问题。高斯模型假设这些一个特征的所有属于某个类别的观测值符合高斯分布,也就是:
下面看一个sklearn中的示例:
>>> from sklearn import datasets
>>> iris = datasets.load_iris()
>>> iris.feature_names # 四个特征的名字
['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)']
>>> iris.data
array([[ 5.1, 3.5, 1.4, 0.2],
[ 4.9, 3. , 1.4, 0.2],
[ 4.7, 3.2, 1.3, 0.2],
[ 4.6, 3.1, 1.5, 0.2],
[ 5. , 3.6, 1.4, 0.2],
[ 5.4, 3.9, 1.7, 0.4],
[ 4.6, 3.4, 1.4, 0.3],
[ 5. , 3.4, 1.5, 0.2],
......
[ 6.5, 3. , 5.2, 2. ],
[ 6.2, 3.4, 5.4, 2.3],
[ 5.9, 3. , 5.1, 1.8]]) #类型是numpy.array
>>> iris.data.size
600 #共600/4=150个样本
>>> iris.target_names
array(['setosa', 'versicolor', 'virginica'],
dtype='|S10')
>>> iris.target
array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,....., 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, ......, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2])
>>> iris.target.size
150
>>> from sklearn.naive_bayes import GaussianNB
>>> clf = GaussianNB()
>>> clf.fit(iris.data, iris.target)
>>> clf.predict(iris.data[0])
array([0]) # 预测正确
>>> clf.predict(iris.data[149])
array([2]) # 预测正确
>>> data = numpy.array([6,4,6,2])
>>> clf.predict(data)
array([2]) # 预测结果很合理
多项式模型
该模型常用于文本分类,特征是单词,值是单词的出现次数。
其中,是类别下特征出现的总次数;是类别下所有特征出现的总次数。对应到文本分类里,如果单词word在一篇分类为label1的文档中出现了5次,那么的值会增加5。如果是去除了重复单词的,那么的值会增加1。是特征的数量,在文本分类中就是去重后的所有单词的数量。的取值范围是[0,1],比较常见的是取值为1。
待预测样本中的特征在训练时可能没有出现,如果没有出现,则值为0,如果直接拿来计算该样本属于某个分类的概率,结果都将是0。在分子中加入,在分母中加入可以解决这个问题。
下面的代码来自sklearn的示例:
>>> import numpy as np
>>> X = np.random.randint(5, size=(6, 100))
>>> y = np.array([1, 2, 3, 4, 5, 6])
>>> from sklearn.naive_bayes import MultinomialNB
>>> clf = MultinomialNB()
>>> clf.fit(X, y)
MultinomialNB(alpha=1.0, class_prior=None, fit_prior=True)
>>> print(clf.predict(X[2]))
[3]
值得注意的是,多项式模型在训练一个数据集结束后可以继续训练其他数据集而无需将两个数据集放在一起进行训练。在sklearn中,MultinomialNB()类的partial_fit()方法可以进行这种训练。这种方式特别适合于训练集大到内存无法一次性放入的情况。
在第一次调用partial_fit()时需要给出所有的分类标号。
>>> import numpy
>>> from sklearn.naive_bayes import MultinomialNB
>>> clf = MultinomialNB()
>>> clf.partial_fit(numpy.array([1,1]), numpy.array(['aa']), ['aa','bb'])
GaussianNB()
>>> clf.partial_fit(numpy.array([6,1]), numpy.array(['bb']))
GaussianNB()
>>> clf.predict(numpy.array([9,1]))
array(['bb'],
dtype='|S2')
伯努利模型
伯努利模型中,对于一个样本来说,其特征用的是全局的特征。
在伯努利模型中,每个特征的取值是布尔型的,即true和false,或者1和0。在文本分类中,就是一个特征有没有在一个文档中出现。
如果特征值值为1,那么
如果特征值值为0,那么
这意味着,“没有某个特征”也是一个特征。
下面的示例来自sklearn官方文档:
>>> import numpy as np
>>> X = np.random.randint(2, size=(6, 100))
>>> Y = np.array([1, 2, 3, 4, 4, 5])
>>> from sklearn.naive_bayes import BernoulliNB
>>> clf = BernoulliNB()
>>> clf.fit(X, Y)
BernoulliNB(alpha=1.0, binarize=0.0, class_prior=None, fit_prior=True)
>>> print(clf.predict(X[2]))
[3]
BernoulliNB()类也有partial_fit()函数。
多项式模型和伯努利模型在文本分类中的应用
在基于naive bayes的文本分类算法给出了很好的解释。
在多项式模型中:
在多项式模型中, 设某文档d=(t1,t2,…,tk),tk是该文档中出现过的单词,允许重复,则
先验概率P(c)= 类c下单词总数/整个训练样本的单词总数
类条件概率P(tk|c)=(类c下单词tk在各个文档中出现过的次数之和+1)/(类c下单词总数+|V|)
V是训练样本的单词表(即抽取单词,单词出现多次,只算一个),|V|则表示训练样本包含多少种单词。 P(tk|c)可以看作是单词tk在证明d属于类c上提供了多大的证据,而P(c)则可以认为是类别c在整体上占多大比例(有多大可能性)。
在伯努利模型中:
P(c)= 类c下文件总数/整个训练样本的文件总数
P(tk|c)=(类c下包含单词tk的文件数+1)/(类c下单词总数+2)
参考
http://scikit-learn.org/stable/modules/naive_bayes.html
http://scikit-learn.org/stable/modules/generated/sklearn.naive_bayes.GaussianNB.html
http://scikit-learn.org/stable/modules/generated/sklearn.naive_bayes.MultinomialNB.html
http://scikit-learn.org/stable/modules/generated/sklearn.naive_bayes.BernoulliNB.html
http://cn.soulmachine.me/blog/20100528/
朴素贝叶斯(Naive Bayes)是一种简单的分类算法,它的经典应用案例为人所熟知:文本分类(如垃圾邮件过滤)。很多教材都从这些案例出发,本文就不重复这些内容了,而把重点放在理论推导(其实很浅显,别被“理论”吓到),三种常用模型及其编码实现(Python)。
如果你对理论推导过程不感兴趣,可以直接逃到三种常用模型及编码实现部分,但我建议你还是看看理论基础部分。
另外,本文的所有代码都可以从我的github获取
1. 朴素贝叶斯的理论基础
朴素贝叶斯算法是基于贝叶斯定理与特征条件独立假设的分类方法。
这里提到的贝叶斯定理、特征条件独立假设就是朴素贝叶斯的两个重要的理论基础。
1.1 贝叶斯定理
先看什么是条件概率。
P(A|B)表示事件B已经发生的前提下,事件A发生的概率,叫做事件B发生下事件A的条件概率。其基本求解公式为:P(A|B)=P(AB)P(B)P(A|B)=P(AB)P(B)
贝叶斯定理便是基于条件概率,通过P(A|B)来求P(B|A):
P(B|A)=P(A|B)P(B)P(A)P(B|A)=P(A|B)P(B)P(A)
顺便提一下,上式中的分母P(A),可以根据全概率公式分解为:
P(A)=∑ni=1P(Bi)P(A|Bi)P(A)=∑i=1nP(Bi)P(A|Bi)
1.2 特征条件独立假设
这一部分开始朴素贝叶斯的理论推导,从中你会深刻地理解什么是特征条件独立假设。
给定训练数据集(X,Y),其中每个样本x都包括n维特征,即x=(x1,x2,x3,...,xn)x=(x1,x2,x3,...,xn),类标记集合含有k种类别,即y=(y1,y2,...,yk)y=(y1,y2,...,yk)。
如果现在来了一个新样本x,我们要怎么判断它的类别?从概率的角度来看,这个问题就是给定x,它属于哪个类别的概率最大。那么问题就转化为求解P(y1|x),P(y2|x),...,P(yk|x)P(y1|x),P(y2|x),...,P(yk|x)中最大的那个,即求后验概率最大的输出:argmaxykP(yk|x)argmaxykP(yk|x)
那P(yk|x)P(yk|x)怎么求解?答案就是贝叶斯定理:
P(yk|x)=P(x|yk)P(yk)P(x)P(yk|x)=P(x|yk)P(yk)P(x)
根据全概率公式,可以进一步地分解上式中的分母:
P(yk|x)=P(x|yk)P(yk)∑kP(x|yk)P(yk)P(yk|x)=P(x|yk)P(yk)∑kP(x|yk)P(yk) 【公式1】
这里休息两分钟
先不管分母,分子中的P(yk)P(yk)是先验概率,根据训练集就可以简单地计算出来。
而条件概率P(x|yk)=P(x1,x2,...,xn|yk)P(x|yk)=P(x1,x2,...,xn|yk),它的参数规模是指数数量级别的,假设第i维特征xixi可取值的个数有SiSi个,类别取值个数为k个,那么参数个数为:k∏ni=1Sik∏i=1nSi
这显然不可行。针对这个问题,朴素贝叶斯算法对条件概率分布作出了独立性的假设,通俗地讲就是说假设各个维度的特征x1,x2,...,xnx1,x2,...,xn互相独立,在这个假设的前提上,条件概率可以转化为:
P(x|yk)=P(x1,x2,...,xn|yk)=∏ni=1P(xi|yk)P(x|yk)=P(x1,x2,...,xn|yk)=∏i=1nP(xi|yk) 【公式2】
这样,参数规模就降到∑ni=1Sik∑i=1nSik
以上就是针对条件概率所作出的特征条件独立性假设,至此,先验概率P(yk)P(yk)和条件概率P(x|yk)P(x|yk)的求解问题就都解决了,那么我们是不是可以求解我们所要的后验概率P(yk|x)P(yk|x)了?
这里思考两分钟
答案是肯定的。我们继续上面关于P(yk|x)P(yk|x)的推导,将【公式2】代入【公式1】得到:
P(yk|x)=P(yk)∏ni=1P(xi|yk)∑kP(yk)∏ni=1P(xi|yk)P(yk|x)=P(yk)∏i=1nP(xi|yk)∑kP(yk)∏i=1nP(xi|yk)
于是朴素贝叶斯分类器可表示为:
f(x)=argmaxykP(yk|x)=argmaxykP(yk)∏ni=1P(xi|yk)∑kP(yk)∏ni=1P(xi|yk)f(x)=argmaxykP(yk|x)=argmaxykP(yk)∏i=1nP(xi|yk)∑kP(yk)∏i=1nP(xi|yk)
因为对所有的ykyk,上式中的分母的值都是一样的(为什么?注意到全加符号就容易理解了),所以可以忽略分母部分,朴素贝叶斯分类器最终表示为:
f(x)=argmaxP(yk)∏ni=1P(xi|yk)f(x)=argmaxP(yk)∏i=1nP(xi|yk)
关于P(yk)P(yk),P(xi|yk)P(xi|yk)的求解,有以下三种常见的模型.
2. 三种常见的模型及编程实现
2.1 多项式模型
当特征是离散的时候,使用多项式模型。多项式模型在计算先验概率P(yk)P(yk)和条件概率P(xi|yk)P(xi|yk)时,会做一些平滑处理,具体公式为:
P(yk)=Nyk+αN+kαP(yk)=Nyk+αN+kα
N是总的样本个数,k是总的类别个数,NykNyk是类别为ykyk的样本个数,αα是平滑值。
P(xi|yk)=Nyk,xi+αNyk+nαP(xi|yk)=Nyk,xi+αNyk+nα
NykNyk是类别为ykyk的样本个数,n是特征的维数,Nyk,xiNyk,xi是类别为ykyk的样本中,第i维特征的值是xixi的样本个数,αα是平滑值。
当α=1α=1时,称作Laplace平滑,当0<α<10<α<1时,称作Lidstone平滑,α=0α=0时不做平滑。
如果不做平滑,当某一维特征的值xixi没在训练样本中出现过时,会导致P(xi|yk)=0P(xi|yk)=0,从而导致后验概率为0。加上平滑就可以克服这个问题。
2.1.1 举例
有如下训练数据,15个样本,2维特征X1,X2X1,X2,2种类别-1,1。给定测试样本x=(2,S)Tx=(2,S)T,判断其类别。
解答如下:
运用多项式模型,令α=1α=1
- 计算先验概率
- 计算各种条件概率
- 对于给定的x=(2,S)Tx=(2,S)T,计算:
由此可以判定y=-1。
2.1.2 编程实现(基于Python,Numpy)
从上面的实例可以看到,当给定训练集时,我们无非就是先计算出所有的先验概率和条件概率,然后把它们存起来(当成一个查找表)。当来一个测试样本时,我们就计算它所有可能的后验概率,最大的那个对应的就是测试样本的类别,而后验概率的计算无非就是在查找表里查找需要的值。
我的代码就是根据这个思想来写的。定义一个MultinomialNB类,它有两个主要的方法:fit(X,y)和predict(X)。fit方法其实就是训练,调用fit方法时,做的工作就是构建查找表。predict方法就是预测,调用predict方法时,做的工作就是求解所有后验概率并找出最大的那个。此外,类的构造函数__init__()中,允许设定αα的值,以及设定先验概率的值。具体代码及如下:
"""
Created on 2015/09/06
@author: wepon (http://2hwp.com)
API Reference: http://scikit-learn.org/stable/modules/naive_bayes.html#naive-bayes
"""
import numpy as np
class MultinomialNB(object):
"""
Naive Bayes classifier for multinomial models
The multinomial Naive Bayes classifier is suitable for classification with
discrete features
Parameters
----------
alpha : float, optional (default=1.0)
Setting alpha = 0 for no smoothing
Setting 0 < alpha < 1 is called Lidstone smoothing
Setting alpha = 1 is called Laplace smoothing
fit_prior : boolean
Whether to learn class prior probabilities or not.
If false, a uniform prior will be used.
class_prior : array-like, size (n_classes,)
Prior probabilities of the classes. If specified the priors are not
adjusted according to the data.
Attributes
----------
fit(X,y):
X and y are array-like, represent features and labels.
call fit() method to train Naive Bayes classifier.
predict(X):
"""
def __init__(self,alpha=1.0,fit_prior=True,class_prior=None):
self.alpha = alpha
self.fit_prior = fit_prior
self.class_prior = class_prior
self.classes = None
self.conditional_prob = None
def _calculate_feature_prob(self,feature):
values = np.unique(feature)
total_num = float(len(feature))
value_prob = {}
for v in values:
value_prob[v] = (( np.sum(np.equal(feature,v)) + self.alpha ) /( total_num + len(values)*self.alpha))
return value_prob
def fit(self,X,y):
#TODO: check X,y
self.classes = np.unique(y)
#calculate class prior probabilities: P(y=ck)
if self.class_prior == None:
class_num = len(self.classes)
if not self.fit_prior:
self.class_prior = [1.0/class_num for _ in range(class_num)] #uniform prior
else:
self.class_prior = []
sample_num = float(len(y))
for c in self.classes:
c_num = np.sum(np.equal(y,c))
self.class_prior.append((c_num+self.alpha)/(sample_num+class_num*self.alpha))
#calculate Conditional Probability: P( xj | y=ck )
self.conditional_prob = {} # like { c0:{ x0:{ value0:0.2, value1:0.8 }, x1:{} }, c1:{...} }
for c in self.classes:
self.conditional_prob[c] = {}
for i in range(len(X[0])): #for each feature
feature = X[np.equal(y,c)][:,i]
self.conditional_prob[c][i] = self._calculate_feature_prob(feature)
return self
#given values_prob {value0:0.2,value1:0.1,value3:0.3,.. } and target_value
#return the probability of target_value
def _get_xj_prob(self,values_prob,target_value):
return values_prob[target_value]
#predict a single sample based on (class_prior,conditional_prob)
def _predict_single_sample(self,x):
label = -1
max_posterior_prob = 0
#for each category, calculate its posterior probability: class_prior * conditional_prob
for c_index in range(len(self.classes)):
current_class_prior = self.class_prior[c_index]
current_conditional_prob = 1.0
feature_prob = self.conditional_prob[self.classes[c_index]]
j = 0
for feature_i in feature_prob.keys():
current_conditional_prob *= self._get_xj_prob(feature_prob[feature_i],x[j])
j += 1
#compare posterior probability and update max_posterior_prob, label
if current_class_prior * current_conditional_prob > max_posterior_prob:
max_posterior_prob = current_class_prior * current_conditional_prob
label = self.classes[c_index]
return label
#predict samples (also single sample)
def predict(self,X):
#TODO1:check and raise NoFitError
#ToDO2:check X
if X.ndim == 1:
return self._predict_single_sample(X)
else:
#classify each sample
labels = []
for i in range(X.shape[0]):
label = self._predict_single_sample(X[i])
labels.append(label)
return labels
我们用上面举的例子来检验一下,注意S,M,L我这里用4,5,6替换:
import numpy as np
X = np.array([
[1,1,1,1,1,2,2,2,2,2,3,3,3,3,3],
[4,5,5,4,4,4,5,5,6,6,6,5,5,6,6]
])
X = X.T
y = np.array([-1,-1,1,1,-1,-1,-1,1,1,1,1,1,1,1,-1])
nb = MultinomialNB(alpha=1.0,fit_prior=True)
nb.fit(X,y)
print nb.predict(np.array([2,4]))#输出-1
2.2 高斯模型
当特征是连续变量的时候,运用多项式模型就会导致很多P(xi|yk)=0P(xi|yk)=0(不做平滑的情况下),此时即使做平滑,所得到的条件概率也难以描述真实情况。所以处理连续的特征变量,应该采用高斯模型。
2.2.1 通过一个例子来说明:
下面是一组人类身体特征的统计资料。
| 性别 | 身高(英尺) | 体重(磅) | 脚掌(英寸) |
|---|---|---|---|
| 男 | 6 | 180 | 12 |
| 男 | 5.92 | 190 | 11 |
| 男 | 5.58 | 170 | 12 |
| 男 | 5.92 | 165 | 10 |
| 女 | 5 | 100 | 6 |
| 女 | 5.5 | 150 | 8 |
| 女 | 5.42 | 130 | 7 |
| 女 | 5.75 | 150 | 9 |
已知某人身高6英尺、体重130磅,脚掌8英寸,请问该人是男是女?
根据朴素贝叶斯分类器,计算下面这个式子的值。
P(身高|性别) x P(体重|性别) x P(脚掌|性别) x P(性别)这里的困难在于,由于身高、体重、脚掌都是连续变量,不能采用离散变量的方法计算概率。而且由于样本太少,所以也无法分成区间计算。怎么办?
这时,可以假设男性和女性的身高、体重、脚掌都是正态分布,通过样本计算出均值和方差,也就是得到正态分布的密度函数。有了密度函数,就可以把值代入,算出某一点的密度函数的值。
比如,男性的身高是均值5.855、方差0.035的正态分布。所以,男性的身高为6英尺的概率的相对值等于1.5789(大于1并没有关系,因为这里是密度函数的值,只用来反映各个值的相对可能性)。
对于脚掌和体重同样可以计算其均值与方差。有了这些数据以后,就可以计算性别的分类了。
P(身高=6|男) x P(体重=130|男) x P(脚掌=8|男) x P(男)
= 6.1984 x e-9
P(身高=6|女) x P(体重=130|女) x P(脚掌=8|女) x P(女)
= 5.3778 x e-4可以看到,女性的概率比男性要高出将近10000倍,所以判断该人为女性。
- 总结
高斯模型假设每一维特征都服从高斯分布(正态分布):
P(xi|yk)=12πσ2yk,i√e−(xi−μyk,i)22σ2yk,iP(xi|yk)=12πσyk,i2e−(xi−μyk,i)22σyk,i2
μyk,iμyk,i表示类别为ykyk的样本中,第i维特征的均值。
σ2yk,iσyk,i2表示类别为ykyk的样本中,第i维特征的方差。
2.2.2 编程实现
高斯模型与多项式模型唯一不同的地方就在于计算 P(xi|yk)P(xi|yk),高斯模型假设各维特征服从正态分布,需要计算的是各维特征的均值与方差。所以我们定义GaussianNB类,继承自MultinomialNB并且重载相应的方法即可。代码如下:
#GaussianNB differ from MultinomialNB in these two method:
# _calculate_feature_prob, _get_xj_prob
class GaussianNB(MultinomialNB):
"""
GaussianNB inherit from MultinomialNB,so it has self.alpha
and self.fit() use alpha to calculate class_prior
However,GaussianNB should calculate class_prior without alpha.
Anyway,it make no big different
"""
#calculate mean(mu) and standard deviation(sigma) of the given feature
def _calculate_feature_prob(self,feature):
mu = np.mean(feature)
sigma = np.std(feature)
return (mu,sigma)
#the probability density for the Gaussian distribution
def _prob_gaussian(self,mu,sigma,x):
return ( 1.0/(sigma * np.sqrt(2 * np.pi)) *
np.exp( - (x - mu)**2 / (2 * sigma**2)) )
#given mu and sigma , return Gaussian distribution probability for target_value
def _get_xj_prob(self,mu_sigma,target_value):
return self._prob_gaussian(mu_sigma[0],mu_sigma[1],target_value)
2.3 伯努利模型
与多项式模型一样,伯努利模型适用于离散特征的情况,所不同的是,伯努利模型中每个特征的取值只能是1和0(以文本分类为例,某个单词在文档中出现过,则其特征值为1,否则为0).
伯努利模型中,条件概率P(xi|yk)P(xi|yk)的计算方式是:
当特征值xixi为1时,P(xi|yk)=P(xi=1|yk)P(xi|yk)=P(xi=1|yk);
当特征值xixi为0时,P(xi|yk)=1−P(xi=1|yk)P(xi|yk)=1−P(xi=1|yk);
2.3.1 编程实现
伯努利模型和多项式模型是一致的,BernoulliNB需要比MultinomialNB多定义一个二值化的方法,该方法会接受一个阈值并将输入的特征二值化(1,0)。当然也可以直接采用MultinomialNB,但需要预先将输入的特征二值化。写到这里不想写了,编程实现留给读者吧。
3 参考文献
- 《统计学习方法》,李航
- 《机器学习》,Tom M.Mitchell
- 维基百科Sex classification
- 朴素贝叶斯的三个常用模型:高斯、多项式、伯努利
- 朴素贝叶斯分类器的应用
- 数学之美番外篇:平凡而又神奇的贝叶斯方法
转载请注明出处,多谢:http://blog.csdn.net/u012162613/article/details/48323777