非線形方程式を解く一般的な方法

公式法

：一般的な形式の単項二次方程式のための\（AX + BX + C ^ 2 = 0 \）

二つの実数式VED方程式を見つけるために使用することができる\（X = \ {FRAC -b + \ SQRT {^ B} 2Aの2-4ac。}} {\）、の合計2 \（X_1 + X_2 = - \ {B} {FRAC} \）、両者の積\（X_1 = X_2 * \ FRAC {C} {A} \）、Δ<0、得られた不等2つの虚根なら\（ = X \ FRAC {-b + IがSQRT {\ 4AC-B ^ {2}}} 2（a）の\）、立方式カルタン式および盛Jingong式。

ハーフ近似

所定の間隔の二次式f（X）の[a、b]は、fは（A）<0、fは（B）> 0、次のように近似することができる場合。

もし\（F（\ FRAC {A + B} {2}）= 0 \）、次いで（\ \ FRAC {A + B }、{2} \）はゼロです。
もし\（F（\ FRAC {A + B} {2}）<0 \）、区間内のゼロ\（[\ FRAC {A + B}、{2}、B] \）、注文\（= \ FRAC {A + B}、{2} \）、ステップ1開始決意から続けます。
もし\（F（\ FRAC {A + B} {2}）> 0 \）、区間内のゼロ\（[\のFRAC { A + B} {2}] \）、注文\（B = \ FRAC {A + B}、{2} \）、ステップ1開始決意から続けます。

典型的には、プロセスは、バイナリ近似を終了することができる可能にする近似の精度限りゼロの範囲です。二分法の制限は、複雑な根と根を再計算することができないことです。

ニュートン反復法

ニュートンのプリンキピアMathematicaの反復法

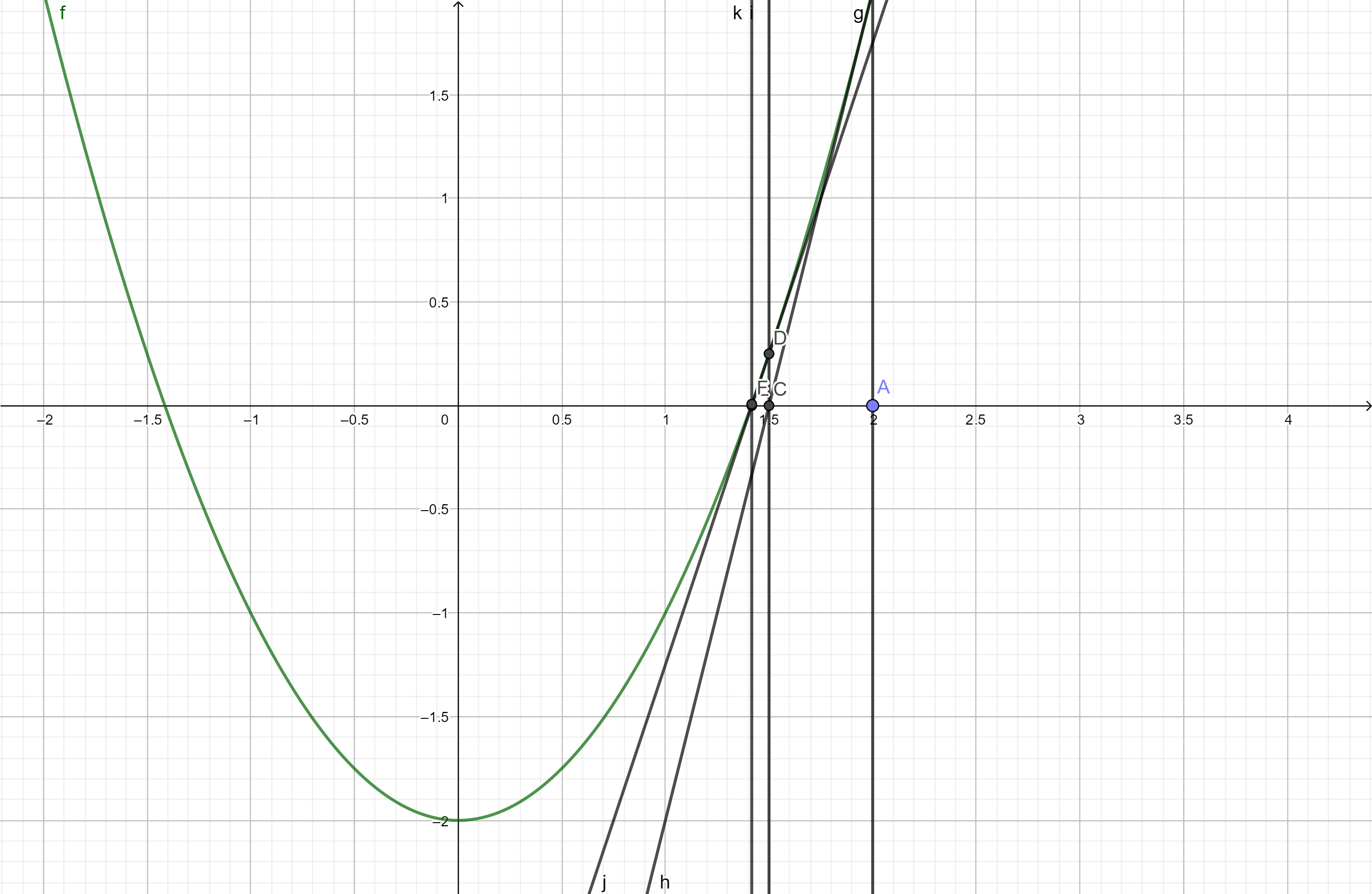
ニュートン反復法

x軸は、点検索する\を（X_0 \）、ポイントを介して\（X_0 \） x軸垂直行うため、ポストに垂直\（F（X）\）の点で\（F（X_0）\）、その後、別の\ （F（X_0）\）点のX軸との接線の交点を得るために、正接関数を実行は、と呼ばれる（1 + N-X_ {} \）\、サイクルは、最終的にルートの近似が得られ、継続されています。

\ [X_ {N + 1} = x_nに関する - \ FRAC {F（x_nに関する）} {F '（x_nに関する）} \]

この方法はまた、このような要件として、値の平方根に使用することができる\（\ SQRT C \）値、関数を構成することができる（F（X）= X ^ 2 -C \）\、右である、すなわち、この関数の根を見つけます。 $ \ sqrtのCは$ aの値を取得します。式を使用して、

\ [设x_nに関する= T、则X_ {N + 1} = T - FRAC \ {T ^ 2 - C} {2トン} = FRAC \ {T + \ FRAC {C}、{T}} {2} \]

得られた\（X_ {N + 1} \）式に新しいTと、誤差が一定値未満であり、その後回答を返すまで、tはその値の平方根です。T = Cは、計算しやすい初期を作ることができます。次のようにこの関数のコードは次のとおりです。

public static double sqrt(double c) {
    if(c < 0)
        return Double.NaN;
    double err = 1e-15;
    double t = c;
    while(Math.abs(t-c/t) > err*t)
        t = (c/t+t) / 2.0;
    return t;
}