Por ejemplo: una clase para aprender un total de 100, de los cuales el 30% de la gran cantidad de ramas colgantes, cables ramas en nombre de 25% que cuelgan, a continuación, el elevado número de ramas que cuelgan de los estudiantes, las familias de la probabilidad algebraica está relacionada con la cantidad? (Nota: el número de alta y el álgebra, mientras que las ramas que cuelgan, ¿cuál es la probabilidad de que hay una diferencia, la diferencia es que uno es, al mismo tiempo toda la clase de colgar tasa de ramas, que es el espacio muestral es toda la clase 100 estudiantes, mientras que el título espacio muestral es alto número de ramas que cuelgan)
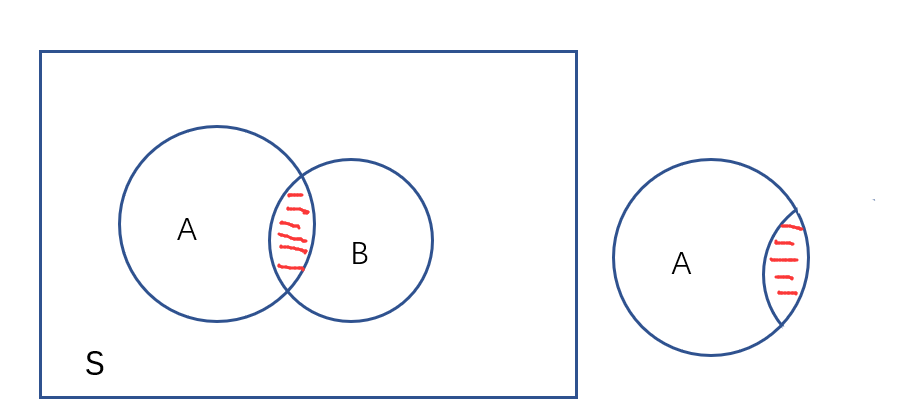
espacio total de la muestra es: s = 100
probabilidad una de la prueba: el elevado número de ramas que cuelgan probabilidad = 30%
probabilidad de eventos B: línea representa colgar las ramas probabilidad = 25%
en el caso de las ramas que cuelgan de la una, evento B la probabilidad es la probabilidad condicional P (B | a) =
\ ({P \ left (B \ left |. A \ left) = \ frac {left {P \ (AB \ right)}} {{P \ left (A \ right)}} \ right \ right \ derecha. .} \)
es decir, la intersección de a y B dividido por el espacio de unos puntos de muestra.
Ejemplos: se proporcionan seis balón cuadro rojo, cuatro blanco. Extracción sin sustitución, cada uno puede tomar un total extraído dos veces.
1) para tomar la bola blanca primero conocido, requiere el cálculo de una segunda probabilidad de bola roja.
2) tomada para encontrar la primera bola blanca, la segunda probabilidad de conseguir la bola roja.
Una hipótesis para el caso de tomar la bola roja, "tomar la bola roja" por primera vez como A1, el segundo bombear el balón a A2. En comparación con el evento correspondiente A "para obtener bola blanca"
probabilidad 1 en cuestión de tomar la bola roja primero, entonces los nueve bolas restantes, tomadas en bola roja 9, a saber:
\ ([{P \ left (\ texto {} A \ mathop {{ }} \ NoLimits _ {{2}} \ left | \ overline \ mathop {{}} \ nolimits {A} _ {{1}} \ left) = \ frac {{6}} { {9}} = \ frac {
{2}} {{3}} \ right \ right \ right} \) ... la diferencia entre los dos problemas es un problema: las condiciones de un problema a un "conocido", se describe . la pregunta 2 se calcula el cálculo paso Común.
\ ({\ begin {la matriz} {* {20} es {L}} {P \ left (\ text {} \ overline {a} \ mathop {{}} \ NoLimits _ {{1}} A \ mathop {{}} \ nolimits _ {{2}} \ left) = P \ left (\ text {} \ overline {A} \ mathop {{}} \ nolimits _ {{1} } \ left) \ P veces \ left (\ texto {} A \ mathop {{}} \ nolimits _ {{2}} \ left | \ overline {A} \ mathop {{}} \ nolimits _ {{1}} \ izquierda) = \ frac {{4 }} {{10}} \ times \ frac {{2}} {{3}} = \ frac {{4}} {{15}} \ right. \ right. \ right . \ right. \ right. \ derecha. \ right.} \\ {\ text {} \ text {} \ text {}} \ end {array}} \)
Ejemplo 2: Supongamos que hay tres billetes de lotería, de los cuales sólo uno es ganar la lotería, los tres estudiantes existentes en vez atraídos sin reemplazo, pedir a un compañero de clase, finalmente, ganar la probabilidad es menor que los otros estudiantes.
Proporcionan X = no ganó, Y = ganar
espacio muestral s = {YXX, xyx, XXY }, sólo tres casos. Por último, una probabilidad de ganar es de 1/3
pero se sabe que los estudiantes no ganó el primero uno, luego el resto del espacio muestral es 2, la probabilidad de ganar en esta ocasión último es un medio
Naturaleza de la probabilidad condicional de
1) un no negativo: Para cada evento B, hay P (B | A)> 0
2) especificaciones: para la inevitable evento s, hay P (S | A) = 1
3) se puede añadir a la columna. de: Let B1, B2 ... pairwise eventos mutuamente excluyentes, hay
\ ({\ Begin {array} {* {20} {l}} {P \ left (\ mathop {{\ mathop {{\ taza}} \ límites ^ {{\ infty}}}} \ límites _ {{i = 1}} ^ {{} } B \ mathop {{}} \ nolimits _ {{i}} \ left | A \ left) = {\ mathop {\ sum} \ límites _ {{i = 1}} ^ {{ \ infty}} {P \ left (B \ mathop {{}} ... \ nolimits _ {i} {} \ left | A \ right) \ right}} \ right \ right \ right} \\ {\ text. {} \ text {} \ text
{}} \ end {array}} \) y la probabilidad total de todos los eventos y eventos en = la probabilidad condicional de ocurrencia y.
Multiplicación fórmula
\ ({\ begin {array} {* {20} {l}} {P \ left (AB \ izquierda) = P \ left (B \ left | A \ izquierda) \ times P \ left (A \ right ) \ right. \ right. \
derecha. \ right. \ right.} \\ {\ text {} \ text {} \ text {}} \ end {array}} \) se apreciará que como la probabilidad de simultánea AB = B probabilidad de probabilidad de ocurrencia de todo el espacio de muestra de a * se produce cuando se produce la condición a.
El tipo se puede generalizar para trazar los eventos más eventos. Por ejemplo: Sean A, B, C para el evento, y P (AB)> 0, hay P (ABC) = P (C | AB) P (B | A) P (A)
\ ({\ Begin {array} {* {20} {l}} {P \ left (AB \ izquierda) = P \ left (B \ left | A \ izquierda) \ times P \ left (A \ right) \ derecho. \ right. \ right. \ right. \ right.} \\ {P \ left (B \ left) = 0.4, P \ left (A + B \ left) = 0,5, \ text {求} \ text { P} \ left (A \ left | \ overline {B} \ left) \ text {} \ text {} \ right \ right \ right \ right \ right \ right \ right} {\\....... P \ left (A \ left) = 1-0,5 = 0,5 \ right. \ right.} \\ {P \ left (\ overline {B} \ left) = 1-0,4 = 0 \ text {} 0,6 \ right . \ right} \\ {P \ left (A \ left | \ overline {B} \ left). = \ frac {{P \ left (A \ overline {B} \ right)}} {{P \ left ( \ overline {B} \ right)}} = \ frac {{0.1}} {{0.6}} = \ frac {{1}} {{6}} \ right. \ right. \ right.} \\ {\ texto {}} {\\} \ end {array}} \)

Figura entenderse
\ ({P \ left (A \ overline {B} \ right)} \) = A y B de intersección del evento opuesta, es decir 0,1
第二种办法:公式推导
\ ({P \ left (A \ left | \ overline {B} \ left) = 1-P \ left (\ overline {A} \ left | \ overline {B} \ left) = 1- \ frac {{1-P \ left (A \ taza B \ right)}} {{1-P \ left (B \ right)}} = 1- \ frac {{1-0,5}} {{1 -0,4}} = \ frac {{1}} {{6}} \ right. \ right. \ right. \ right. \ right. \ right.} \)
Ejemplo 2: una contraseña de la tarjeta de ahorros de un total de seis números, cada dígito puede elegir uno de 0-9, retirar dinero en los cajeros automáticos del banco a alguien, olvidar la última contraseña de cuatro dígitos, que buscan
1) de acuerdo con cualquiera de los últimos dígitos, no más de 2 veces para presionar sobre la probabilidad.
Pulse para configurar eventos para el A, por primera vez por A1, A2 de la secundaria por
no más de 2 veces la probabilidad de la prensa, de acuerdo con el primero o segundo par son considerados por no más de 2 veces por derecho.
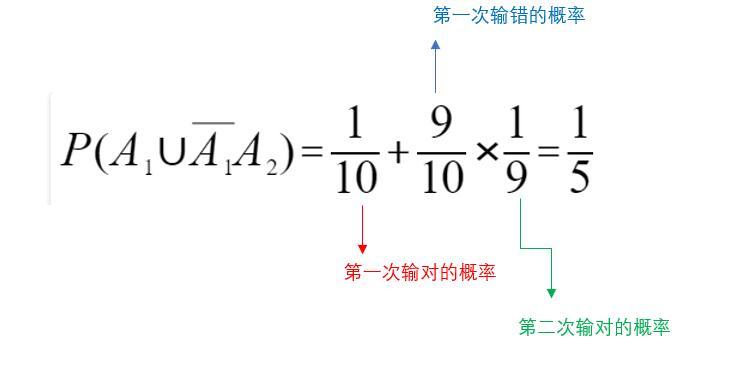
2) Si se acuerda de la contraseña último es un número par, no más de 2 veces a la probabilidad de prensa de la
anterior, es la misma, pero el espacio muestral se convierte {0,2,4,6,8}, un total de cinco palabras
\ ({{P \ left ( \ mathop {{a}} \ nolimits _ {{1}} \ taza \ overline {\ mathop {{a}} \ nolimits _ {{1}}} A \ mathop {{}} \ nolimits _ {{2}} \ izquierda) = \ frac {{1}} {{5}} + \ frac {{4}} {{5}} \ times \ frac {{1}} {{4}} = \ frac {{2}} { {5}} \ right. \ right.}} \)
Ejemplo 3: clase A Curso tasa de fracaso de un 4%, mientras que los estudiantes pasarán 25% de los estudiantes puede esperar A, encontrar la probabilidad de A para dar al estudiante.
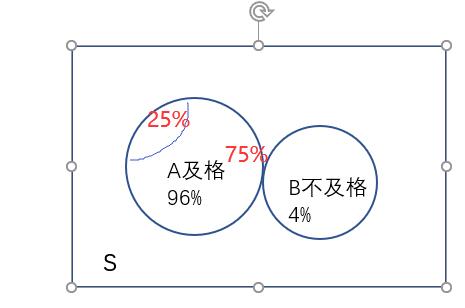
Evento A: tiene A, caso B: Pase
conocida:
\ ({\ Matriz el begin {} {} {L * 20 es {{}} A \ subset B, AB = A, P \ left (AB \ izquierda) = P \ left (A \ right) \ derecha. \ right.} \\ {P \ left (B \ left) = 1-4 \ text {%} = 96 \ text {%} \ right. \ right.} \\ {P \ left (A \ left | B \ left) = 25 \ text {%} \ right \ right \ right ...} \\ {P \ left (AB \ left) = P \ left (B \ left) \ veces P \ left (A \ left | B \ left) = 96 \ text {%} \ times 25 \ text {%} = 0,24 \ right \ right \ right \ right \ right \ right \ ...... derecho.} \ end {array} } \)