Tanto la escuela de frecuencia como la escuela bayesiana resuelven el problema de la inferencia estadística.
La escuela de frecuencia también se llama la escuela clásica. Esta escuela ve un valor fijo para la probabilidad de un evento.
La Escuela Bayesiana ve la probabilidad de un evento como una variable aleatoria.
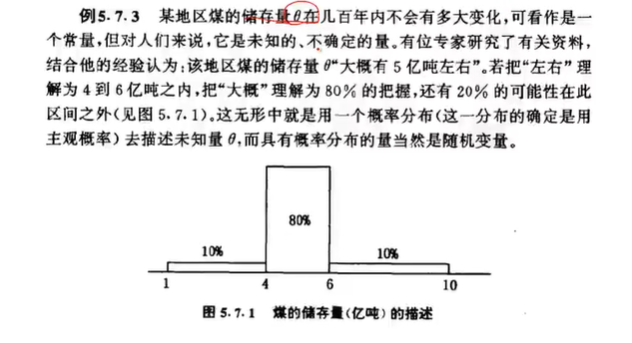
Por ejemplo: en la descripción del almacenamiento de carbón en una mina de carbón, la escuela clásica describe el almacenamiento de carbón A = 10 kg. Bayes describió el almacenamiento de carbón A en aproximadamente 10 kg, y luego, basándose en datos históricos u otra información, se estimó que 2 <A <8, la probabilidad es del 80%, y la probabilidad en otros casos es del 20%.
Hay tres puntos principales de inferencia estadística: 1. Análisis de muestreo 2. Estimación de parámetros 3. Prueba de hipótesis. Tres fuentes importantes de información: 1. Información general 2. Información de muestra 3. Información previa
Ambas escuelas utilizan información general e información de muestra, y la escuela bayesiana agrega el uso de esta fuente de información de "información previa" .
Caso estadístico bayesiano 1: Laplace estudió en 1786 si la tasa de natalidad de los bebés varones en París era superior a 0,5.
Paso 1: Función de probabilidad
Suponga que el evento A de un bebé nace, solo hay dos posibilidades. Nacido y no nacido, por lo que se ajusta a la distribución binomial X ~ b (n, p).
Por lo tanto, su tasa de natalidad \ ({P \ left (X = x \ left | \ theta \ left) = C \ mathop {{}} \ nolimits _ {{n}} ^ {{x}} \ theta \ mathop {{}} \ nolimits ^ {{x}} \ left (1- \ theta \ left) \ mathop {{}} \ nolimits ^ {{nx}}, x = 0,1, ..., n \ right. \ right. \ right. \ right. \ right.} \)
Esta es la función de probabilidad, la probabilidad de que ocurra el evento A.
Si es una función de probabilidad estricta, debe convertirse en una distribución vectorial.
\ ({P \ left (\ overline {X} \ left | \ theta \ left) = {\ mathop {\ prod} \ limits _ {{i = 1}} ^ {{n}} {P \ left (x = x \ mathop {{}} \ nolimits _ {{i}} \ left | \ theta \ right) \ right.}} \ right. \ right. \ right.} \)
Segundo paso: condiciones previas
si se determina antes Condiciones, hay un principio que puede usarse aquí. Si no sabe nada sobre un evento, primero puede suponer que el evento se distribuye uniformemente dentro de un cierto intervalo (es decir, el principio de la hipótesis bayesiana: el principio de ignorancia igual y el mismo conocimiento). Según este supuesto, se obtiene la función de distribución previa de θ.
\ ({\ pi \ left (\ theta \ left) {\ left \ {\ begin {array} {* {20} {l}} {1,0 \ le \ theta \ le 1;} \\ {0, otro;} \ end {array} \ right.} \ right. \ right.} \)
Paso 3: Multiplique la función de probabilidad y la función de distribución previa para obtener la función de densidad conjunta.
\ ({h \ left (x, \ theta \ left) = C \ mathop {{}} \ nolimits _ {{n}} ^ {{x}} \ theta \ mathop {{}} \ nolimits ^ {{x} } \ left (1- \ theta \
izquierda) \ mathop {{}} \ nolimits ^ {{nx}}, 0 \ le \ theta \ le 1 \ right. \ right. \ right. \ right.} \) Ver Es lo mismo que la función de probabilidad de cada paso, pero su significado es diferente.
Cuarto punto: encuentre la distribución marginal m (x)
\ ({m \ left (x \ left) = {\ mathop {\ int} \ limits _ {{\ theta}} ^ {{}} {h \ left (x , \ theta \ left) d \ theta \ right. \ right.}} \ right. \ right.} \)
Quinto punto: obtener la distribución posterior (distribución bayesiana)
\ ({\ pi \ left (\ theta \ left | x \ left) = \ frac {{h \ left (x, \ theta \ right)}} { {m \ left (x \ right)}} = \ frac {{P \ left (x \ left | \ theta \ left) \ pi \ left (\ theta \ right) \ right. \ right. \ right.}} {{{\ mathop {\ int} \ limits _ {{\ theta}} ^ {{}} {P \ left ({x \ left | \ theta \ right.} \ right)}} {\ pi \ left (\ theta \ right.} \ text {)} d \ theta}} \ right. \ right. \ right.} \)
Sexto punto: según la muestra limitada, se sustituye en la fórmula de distribución posterior,
como la recopilación de datos y el descubrimiento de 1745 a 1770 Nacido, niño 251527, niña 241945 niña.
\ ({P \ left (\ theta \ le 0.5 \ left | x \ left) = {\ mathop {\ int} \ limits _ {{0}} ^ {{0.5}} \ begin {array} {* {20} {l}} {\ pi \ left (dx \ left) d \ theta = 1.15 \ times 10 \ mathop {{}} \ nolimits ^ {{-42}} \ right. \ right.} \\ {} \ end {array}} \ right. \ right. \ right.} \)
La probabilidad de que θ sea menor que 0.5 es muy pequeña, entonces
\ ({\ theta> 0.5 \ text {YES} \ text {this} \ text {结} \ text {果} \ text {被} \ text {证} \ text {明}} \)