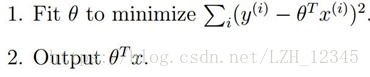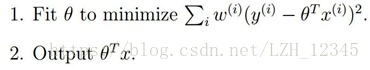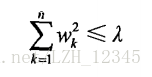《机器学习实战》第八章学习笔记（回归）

一、用线性回归找到最佳拟合直线

1.1 线性回归

回归的目的是预测数值型的目标值。最直接的方法就是找到回归方程Y=X.T*w。其中w称作回归系数，求这些回归系数的过程就是回归。一个常用的方法就是找出使误差最小的w。这里的误差是指预测y值和真实y值之间的平方差值。由于使用该误差的简单累加将使得正差值和负差值相互抵消，所以我们采用平方误差。

回归的一般方法：

收集数据：采用任意方法收集数据。
准备数据：回归需要数值型数据，标称型数据将被转成二值型数据。
分析数据：绘出数据的可视化二维图将有助于对数据做出理解和分析，在采用缩减法求得新回归系数之后, 可以将新拟合线绘在图上作为对比。
训练算法：找到回归系数。
测试算法：使用R^2或者预测值和数据的拟合度，来分析模型的效果。
使用算法：使用回归，可以在给定输入的时候预测出一个数值，这是对分类方法的提升，因为这样可以预测连续型数据而不仅仅是离散的类别标签。

1.2 代码实现

# -*- coding: utf-8 -*-
"""
Created on Fri May  4 15:35:23 2018

@author: lizihua
"""
from numpy import mat,linalg,corrcoef
import matplotlib.pyplot as plt

#加载数据
def loadDataSet(fileName):
    numFeat = len(open(fileName).readline().split('\t'))-1
    dataMat = [];labelMat = []
    fr = open(fileName)
    for line in fr.readlines():
        lineArr = []
        curLine = line.strip().split('\t')
        for i in range(numFeat):
            lineArr.append(float(curLine[i]))
        dataMat.append(lineArr)
        labelMat.append(float(curLine[-1]))
    return dataMat, labelMat

#计算最佳拟合直线
#w的最优解的表达式：w=(X.T*X).I*(X.T*y)
def standRegres(xArr,yArr):
    xMat = mat(xArr); yMat = mat(yArr).T
    xTx = xMat.T*xMat
    #若矩阵的行列式不为零，则该矩阵一定可逆
    #Numpy中的linalg库中的det()方法可以计算矩阵的行列式
    if linalg.det(xTx) == 0.0:
        print("This matrix is singular, cannot do inverse")
        return
    #矩阵A.I代表求矩阵A的逆矩阵
    ws = xTx.I *(xMat.T * yMat)
    return ws

#绘制数据图形
def plot(xArr,yArr,ws):
    xcord=[]
    for i in range(len(xArr)):
        xcord.append(xArr[i][1]) 
    fig = plt.figure()
    ax = fig.add_subplot(111)
    ax.scatter(xcord,yArr, marker='o', s=50)
    yHat = mat(xArr)*ws
    ax.plot(xcord,yHat,'g')
    plt.show()
    return yHat
#测试
if __name__ == "__main__":
    xArr,yArr = loadDataSet('ex0.txt')
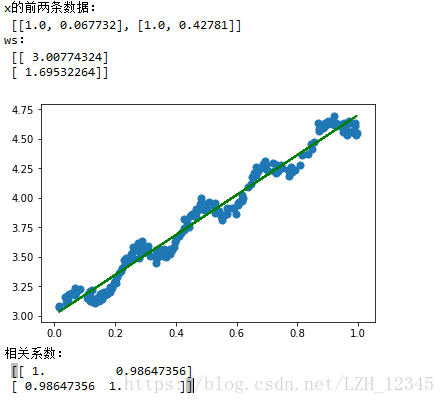
    print("x的前两条数据：\n",xArr[:2])  
    #result:x的前两条数据： [[1.0, 0.067732], [1.0, 0.42781]]
    #注意：x数据中X0总是1
    ws = standRegres(xArr,yArr)
    print("ws：\n",ws)
    yHat = plot(xArr,yArr,ws)
    print("相关系数：\n",corrcoef(yHat.T,yArr))

1.3 结果显示

二、局部加权线性回归（Locally Weighted Linear Regression,LWLR）

局部加权线性回归算法就是我们给待预测点附件的每个点都赋予一定的权重；然后在这个带有权重的新数据集上基于最小均方误差来进行普通的回归。

2.1 基本思想

普通的线性回归：

使得均方误差最小，得：

局部加权线性回归：为权值，从上面可以看出，如果很大，我们将很难使得小，所以如果很小，则它产生的影响就很小

为权值，从上面可以看出，如果很大，我们将很难使得小，所以如果很小，则它产生的影响就很小

使得均方误差最小，得：，其中W是一个矩阵，用来给每个数据点赋予权重

而LWLR使用“核”（与支持向量机的核类似）来对附件的点赋予更高的权重。核的类型可以自由选择，最常用的核就是高斯核，高斯核对应的权重如下：

2.2 代码显示

# -*- coding: utf-8 -*-
"""
Created on Fri May  4 15:35:23 2018

@author: lizihua
"""
from numpy import mat,linalg,corrcoef,shape,eye,exp,zeros
import numpy as np
import matplotlib.pyplot as plt

#加载数据
def loadDataSet(fileName):
    numFeat = len(open(fileName).readline().split('\t'))-1
    dataMat = [];labelMat = []
    fr = open(fileName)
    for line in fr.readlines():
        lineArr = []
        curLine = line.strip().split('\t')
        for i in range(numFeat):
            lineArr.append(float(curLine[i]))
        dataMat.append(lineArr)
        labelMat.append(float(curLine[-1]))
    return dataMat, labelMat

#局部加权线性回归函数
#测试点就是高斯核表达式中的x,xArr为x(i)组成的数组
def lwlr(testPoint,xArr,yArr,k=1.0):
    xMat = mat(xArr); yMat = mat(yArr).T
    m = shape(xMat)[0]
    #创建m*m对角矩阵（对角线为1，其余为0）
    weights = mat(eye(m))
    for j in range(m):
        diffMat = testPoint - xMat[j,:]
        #高斯核权重的计算
        weights[j,j] = exp(diffMat*diffMat.T/(-2.0*k**2))
    xTx = xMat.T * (weights*xMat)
    if linalg.det(xTx) == 0:
        print("This matrix is singular, cannot do inverse")
        return
    ws = xTx.I * (xMat.T * (weights * yMat))
    return testPoint * ws

#为每个测试集中的数据点调用lwlr
def lwlrTest(testArr,xArr,yArr,k=1.0):
    m = shape(testArr)[0]
    yHat =  zeros(m)
    for i in range(m):
        yHat[i] = lwlr(testArr[i],xArr,yArr,k)
    return yHat

#绘制估计点和原始点的拟合效果图
def lwlrPlot(xArr,yArr,yHat,k):
    xMat= mat(xArr)
    #将xMat[:,1](即X1)在axis=0方向（列方向）从小到大排序，并将其索引返回
    strInd = np.argsort(xMat[:,1],axis=0)    #shape(strInd)=(200,1)
    #shape(xMat[strInd])=(200,1,2)    shape(xMat)=(200,2)
    xSort = xMat[strInd][:,0,:]      #将xMat按顺序排列，xSort[:,1]即X1       
    fig = plt.figure()
    ax = fig.add_subplot(111)
    ax.plot(xSort[:,1],yHat[strInd])
    #flatten()函数是将矩阵降低一维，默认降维是按横着排列
    #例如，xMat=matrix([[1,2],[3,4]]) xMat.flatten()=matrix([[1, 2, 3, 4]])
    #xMat.A则是将xMat矩阵转换成数组array,例如：xMat.A = array([[1, 2],[3, 4]])
    ax.scatter(xMat[:,1].flatten().A[0],mat(yArr).T.flatten().A[0],s=2,c='red')
    plt.title("LWLR with k = %s" %k)
    plt.show()

#定义预测误差函数，用于分析预测误差的大小
def rssError(yArr,yHat):
    return ((yArr-yHat)**2).sum()       

#测试
if __name__ == "__main__":
    xArr,yArr = loadDataSet('ex0.txt')
    #局部加权线性回归预测结果展示：
    y0 = lwlr(xArr[0],xArr,yArr,1.0)
    y1 = lwlr(xArr[0],xArr,yArr,0.001)
    print("y0:\n",y0)   #y0:[[ 3.12204471]]
    print("y1:\n",y1)   #y1: [[ 3.20175729]]
    #比较一下k=1.0,0.01,0.003时的拟合效果
    #k=1.0
    yHat1 = lwlrTest(xArr,xArr,yArr,1.0)
    lwlrPlot(xArr,yArr,yHat1,1.0)
    print("k=1.0时，预测误差：",rssError(yArr,yHat1))
    #k=0.01
    yHat2 = lwlrTest(xArr,xArr,yArr,0.01)
    lwlrPlot(xArr,yArr,yHat2,0.01)
    print("k=0.01时，预测误差：",rssError(yArr,yHat2))
    #k=0.003
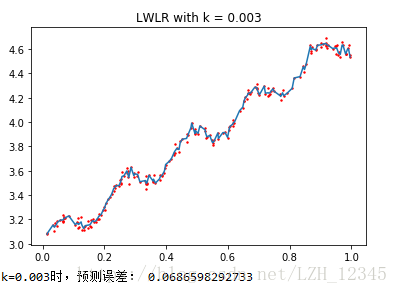
    yHat3 = lwlrTest(xArr,xArr,yArr,0.003)
    lwlrPlot(xArr,yArr,yHat3,0.003)
    print("k=0.003时，预测误差：",rssError(yArr,yHat3))

2.3 结果显示

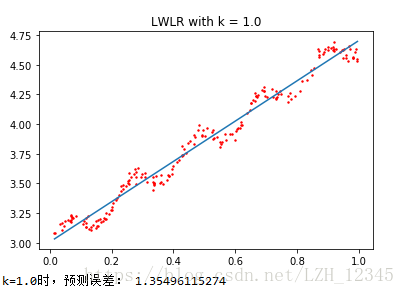
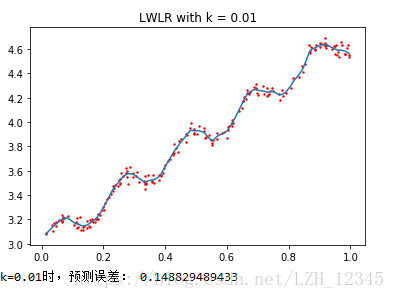
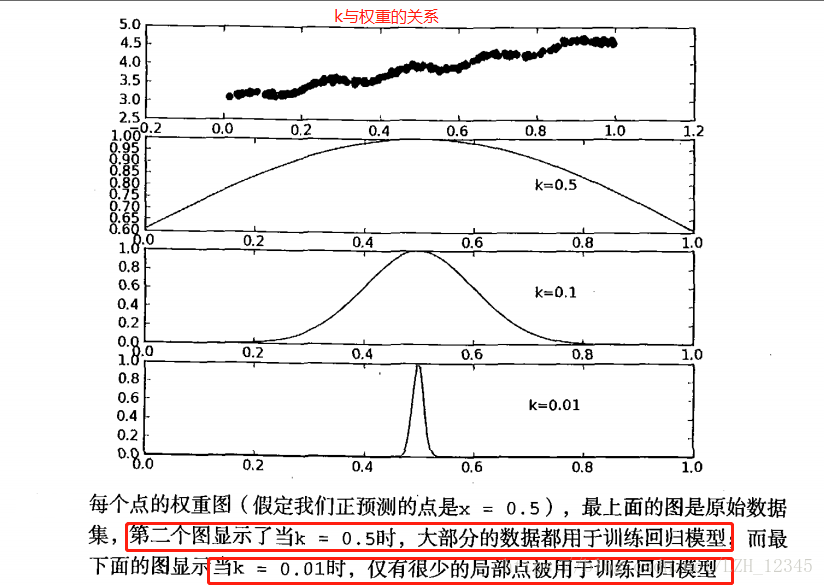
从上图结果可以看出：k=1.0时，模型效果与最小二乘法差不多，k=0.01时，模型效果最好，，可以挖出数据的潜在规律，而k=0.003时，则考虑了太多的噪声，进而导致了过拟合。

局部加权线性回归同样存在一个问题，即增加了计算量，因为它对每一个点做预测时都必须使用整个数据集，k=0.01时可以得到很好的估计，但是，从图中也可以看出，大多数数据点的权重都接近0，若是可以避免这些计算，则可以减少程序运行时间从而缓解因计算量增加带来的问题。

三、岭回归

3.1 基本思想

如果特征比样本点还多（n > m ) ,也就是说输入数据的矩阵X不是满秩矩阵。非满秩矩阵在求逆时会出现问题。为了解决这个问题，统计学家引入了岭回归（ ridgeregression)的概念。

3.2 代码实现

# -*- coding: utf-8 -*-
"""
Created on Fri May  4 15:35:23 2018

@author: lizihua
"""
from numpy import mat,linalg,corrcoef,shape,eye,exp,zeros,mean,var,log
import numpy as np
import matplotlib.pyplot as plt

#加载数据
def loadDataSet(fileName):
    numFeat = len(open(fileName).readline().split('\t'))-1
    dataMat = [];labelMat = []
    fr = open(fileName)
    for line in fr.readlines():
        lineArr = []
        curLine = line.strip().split('\t')
        for i in range(numFeat):
            lineArr.append(float(curLine[i]))
        dataMat.append(lineArr)
        labelMat.append(float(curLine[-1]))
    return dataMat, labelMat

#岭回归
#给定lambda,计算回归系数
def ridgeRegres(xMat,yMat,lam=0.2):
    xTx = xMat.T * xMat    #shape(xTx): (8, 8)   shape(xMat): (4177, 8)
    denom = xTx + eye(shape(xMat)[1])*lam   #shape(denom): (8, 8)
    #因为当lam=0时，可能出现问题，所以，仍需要检查行列式是否为0
    if linalg.det(denom) == 0.0:
        print("This matrix is singular, cannot do inverse")
        return
    ##下面函数在使用yMat时，对其进行的转置，因此，这里不需要转置
    ws = denom.I * (xMat.T * yMat)    #shape(yMat): (1, 4177) 
    return ws

#在一组lambda上测试结果
def ridgeTest(xArr,yArr):
    xMat = mat(xArr);yMat = mat(yArr).T
    yMean = mean(yMat,axis=0)
    #标准化处理（归一化处理），使得每维特征具有相同的重要性
    #归一化公式是：x=(x-mean)/var，最终X符合正态分布
    yMat = yMat-yMean
    xMeans = mean(xMat)
    xVar = var(xMat,0)
    xMat = (xMat-xMeans)/xVar
    numTestPts = 30
    wMat = zeros((numTestPts,shape(xMat)[1]))
    for i in range(numTestPts):
        ws = ridgeRegres(xMat,yMat,exp(i-10))
        wMat[i,:]=ws.T
    return wMat
  

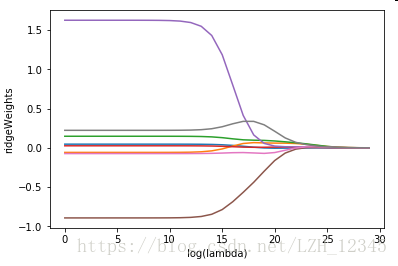
#绘制回归系数与log(lambda)的关系图
def wsAndLamPlot(ws):
    fig = plt.figure()
    ax=fig.add_subplot(111)
    ax.plot(ws)
    plt.xlabel("log(lambda)")
    plt.ylabel("ridgeWeights")
    plt.show()
    
#测试
if __name__ == "__main__":
    abX,abY = loadDataSet("abalone.txt")
    ridgeWeights = ridgeTest(abX,abY)
    wsAndLamPlot(ridgeWeights)

3.3 结果显示

四、lasso

4.1 基本思想

不难证明，在增加如下约束时，普通的最小二乘法回归会得到与岭回归的一样的公式：

4.2 前向逐步回归算法

4.2.1 代码实现

from numpy import mat,linalg,corrcoef,shape,eye,exp,zeros,mean,std,log,var
import numpy as np
import matplotlib.pyplot as plt

#加载数据
def loadDataSet(fileName):
    numFeat = len(open(fileName).readline().split('\t'))-1
    dataMat = [];labelMat = []
    fr = open(fileName)
    for line in fr.readlines():
        lineArr = []
        curLine = line.strip().split('\t')
        for i in range(numFeat):
            lineArr.append(float(curLine[i]))
        dataMat.append(lineArr)
        labelMat.append(float(curLine[-1]))
    return dataMat, labelMat

#前向逐步线性回归

def stageWise(xArr,yArr,eps = 0.01,numIt = 100):
    xMat=mat(xArr);yMat=mat(yArr).T
    yMean = mean(yMat,axis=0)
    #标准化处理（归一化处理），使得每维特征具有相同的重要性
    yMat = yMat-yMean
    xMeans = mean(xMat)
    xVar = var(xMat,0)
    xMat = (xMat-xMeans)/xVar
    m,n = shape(xMat)
    returnMat = zeros((numIt,n))
    ws = zeros((n,1));wsTest = ws.copy();wsMax = ws.copy()
    for i in range(numIt):
        print(ws.T)
        lowestError = np.inf
        for j in range(n):
            for sign in [-1,1]:
                wsTest = ws.copy()
                wsTest[j] += eps*sign
                yTest = xMat * wsTest
                rssE = rssError(yMat.A,yTest.A)
                if rssE < lowestError:
                    lowestError = rssE
                    wsMax = wsTest
        ws = wsMax.copy()
        returnMat[i,:]=ws.T
    return returnMat

#绘制回归系数与迭代次数之间的关系图
def wsAndNumItPlot(ws):
    fig = plt.figure()
    ax=fig.add_subplot(111)
    ax.plot(ws)
    plt.xlabel("NumIt")
    plt.ylabel("Weights")
    plt.show()        
        

#测试
if __name__ == "__main__":
    abX,abY = loadDataSet("abalone.txt")
    returnMat = stageWise(abX,abY,0.001,1000)
    #print("returnMat:\n",returnMat)
    wsAndNumItPlot(returnMat)

4.2.2 部分结果显示

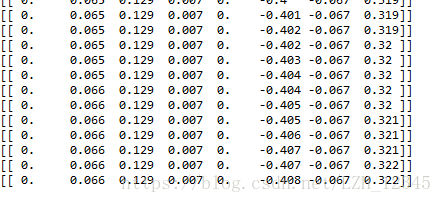
逐步线性回归算法的实际好处并不在于能绘出上图这样漂亮的图，主要的优点在于它可以帮助人们理解现有的模型并做出改进。当构建了一个模型后，可以运行该算法找出重要的特征，这样就有可能及时停止对那些不重要特征的收集。最后，如果用于测试，该算法每100次迭代后就可以构建出一个模型，可以使用类似于10折交叉验证的方法比较这些模型，最终选择使误差最小的模型。

当应用缩减方法（如逐步线性回归或岭回归)时，模型也就增加了偏差（bias)，与此同时却减小了模型的方差。

五、权衡偏差和方差

任何时候，一旦发现模型和测量值之间存在差异，就说出现了误差。当考虑模型中的“ 噪声“或者说误差时，必须考虑其来源。你可能会对复杂的过程进行简化，这将导致在模型和测量值之间出现“ 噪声”或误差，若无法理解数据的真实生成过程，也会导致差异的发生。另外，测量过程本身也可能产生“ 噪声”或者问题。

一般认为，上述两种误差由三个部分组成：偏差、测量误差和随机噪声。在局部线性加权线性回归中，我们通过引入越来越小的核来不断增大模型的方差。

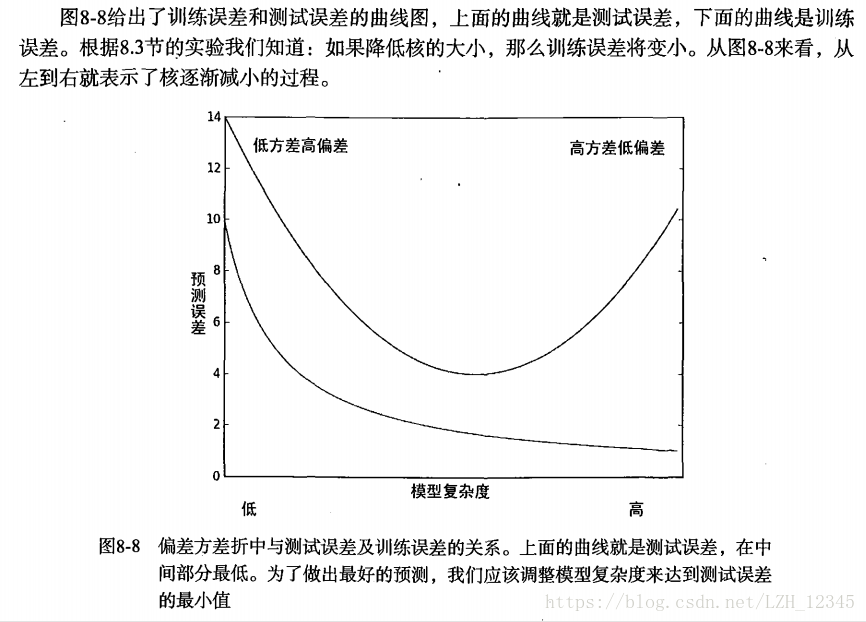
而缩减法，可以将一些系数缩减成很小的值或直接缩减为0，这是一个增大模型偏差的例子。通过把一些特征的回归系数缩减到0，同时也就减少了模型的复杂度。例子中有8个特征，消除其中两个后不仅使模型更易理解，同时还降低了预测误差。图8-8的左侧是参数缩减过于严厉的结果，而右侧是无缩减的效果。
方差是可以度量的。如果从鲍鱼数据中取一个随机样本集（例如取其中100个数据）并用线性模型拟合，将会得到一组回归系数。同理，再取出另一组随机样本集并拟合，将会得到另一组回归系数。这些系数间的差异大小也就是模型方差大小的反映。上述偏差与方差折中的概念在机器学习十分流行并且反复出现。