数学对于计算机图形学的重要性是不言而喻的。在学习Shader之前，首先就要打好数学基础，好在入门Unity Shader所需的数学知识都是线性代数中很基础的的内容。按部就班的来，第一篇文章记录总结的是坐标系，点，矢量等概念以及简单的运算。本文主要源自《Unity Shader入门精要》一书的读书笔记。
如果有小伙伴对Shader着色器相关的概念还不了解的话，可以先看下这篇文章一篇文章搞懂到底什么是渲染流水线
坐标系
在三维笛卡尔坐标系中，我们需要定义3个坐标轴和一个原点。这3个坐标轴被称为该坐标系的基矢量，相互垂直且长度为1的基矢量被称为标准正交基，相互垂直但长度不为1的基矢量被称为正交基
左手坐标系与右手坐标系
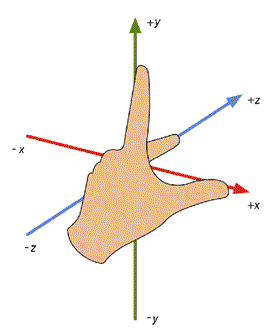
我们可以利用双手来判断一个坐标系的旋向性。请读者举起你的左手，用食指和大拇指摆出一个“L”的手势，并且让你的食指向上，大拇指向右。现在伸出你的中指，它将指向你的前方。此时你已经得到了一个左手坐标系。你的大拇指，食指，中指分别对应了+x，+y，+z轴。如下图所示。
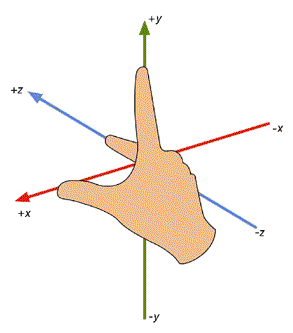
读者可以通过右手得到一个右手坐标系。举起你的右手，这次食指仍然向上，中指指向前方，不同的是，大拇指将指向左侧。如下图所示。
左手法则与右手法则
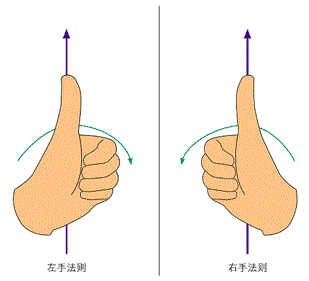
左手坐标系和右手坐标系对于正向旋转的定义也不同，分别取决于左手法则和右手法则。在左手坐标系中，请举起你的左手，握拳，伸出大拇指让它指向旋转轴的正方向，那么旋转的正方向就是剩下4个手指的弯曲方向。在右手坐标系中，使用右手法则对旋转正方向的判断类似。
Unity使用的坐标系
对于模型空间和世界空间，Unity使用的是左手坐标系。
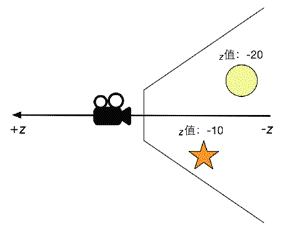
对于观察空间，Unity使用的是右手坐标系。观察空间通俗来讲就是以摄像机为原点的坐标系，摄像机的前向是z轴的负方向，也就是说，z轴坐标的减少意味着场景深度的增加。
点和矢量
点是n维空间中的一个位置。
矢量是指n维空间中一种包含了模和方向的有向线段。而标量只有模没有方向。
具体来讲：
- 矢量的模指的是矢量的长度
- 矢量的方向则描述了这个矢量在空间中的指向
- 一个矢量通常由一个箭头来表示。矢量的头就是指它的箭头处，尾指的是另一个端点处
通常矢量被用于表示相对于某个点的偏移，也就是说只要矢量的模和方向不变，无论放在哪里，都是同一个矢量。
点和矢量的区别
矢量可以用于表示相对于另一个点的位置，此时矢量的尾是一个位置，那么矢量的头就可以表示另一个位置了。如果我们把矢量的尾固定在坐标系原点，那么这个矢量的表示就和点的表示重合了。尽管点和矢量在数学表达式上都是一样的，但区分点和矢量之间的不同是非常重要的。可以这样理解，任何一个点都可以表示成一个从原点位置出发的矢量。
矢量的运算
矢量和标量乘法/除法
我们不能把矢量和标量进行相加/相减的运算（想象一下，你会把矢量速度和标量距离相加吗）。
对矢量和标量进行乘法运算，会得到一个不同长度且可能方向相反的新的矢量。
公式
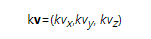
注意：对于乘法来说，矢量和标量的位置可以互换。但对于除法来说，只能是矢量除以标量，而不能是标量除以矢量，这是没有意义的。
几何意义
把一个矢量和一个标量相乘，意味着对矢量进行一个大小为标量的缩放。例如，如果想把一个矢量放大两倍，就乘以2,。当标量小于0时，矢量的方向也会相反。
矢量的加法/减法
我们可以对两个矢量进行相加或相减，其结果是一个相同维度的新矢量
需要注意的是，一个矢量不可以和一个标量相加或相减，也不能和不同维度的矢量进行运算。
公式
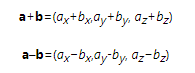
几何意义
在图形学中矢量通常用于描述位置偏移（简称位移）。对于加法，我们可以把矢量a的头连接到矢量b的尾，然后画一条从a的尾到b的头的矢量，来得到a和b相加的矢量。也就是说，如果我们从一个起点进行了一个位置偏移a，然后进行了一个位置偏移b，那么就等同于进行了一个a+b的位置偏移。矢量的减法也是类似的。
假设，空间内有两点a和b。我们可以用矢量a和b来表示它们相对于原点的位移。如果我们想要计算点b相对于a的位移，就可以通过把b和a相减得到。
矢量的模
矢量的模是一个标量，可以理解为是矢量在空间中的长度。
矢量的表示符号通常是在矢量两旁分别加上一条垂直线
公式
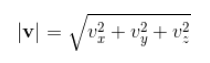
几何意义
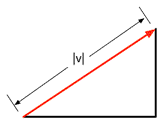
从几何意义上来理解二维矢量，我们可以对任意矢量构建一个三角形，如下图所示。可以看出，其实就是使用了勾股定理，矢量的两个分量的绝对值对应了三角形两个直角边的长度，而斜边的长度就是矢量的模。
单位矢量
在很多情况下，我们只关心矢量的方向而不是模。在这些情况下，我们就需要计算单位矢量。
单位矢量指的是模为1的矢量。单位矢量也被称为归一化的矢量。对任何给定的非零矢量，把它转换成单位矢量的过程被称为归一化。
公式
为了求解单位矢量，我们可以用矢量除以该矢量的模得到。
零矢量（每个分量都是0的矢量）是不可以被归一化的。这是因为做除法运算时分母不能为0.
几何意义
对于二维空间来说，我们可以画一个单位圆（半径为1），那么单位矢量就可以是从圆心出发到圆边界的矢量。在三维空间中，单位矢量就是从一个单位球的球心出发，到达球面的矢量。
矢量的点积
矢量之间也可以进行乘法，矢量的乘法有两种最常用的种类：点积（内积）和叉积（外积）。矢量的点积结果是一个标量
公式
公式1，两个三维矢量的点积是把两个矢量分别对应分量相乘后再取和
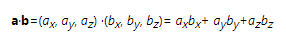
公式2，矢量的点积等于两个矢量的模乘以cosθ(θ表示两个矢量的夹角)
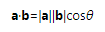
公式2的推导，如下所示。
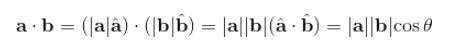
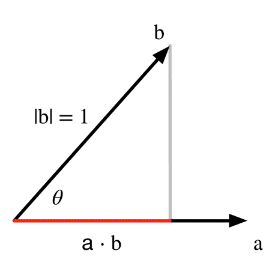
重点是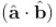
为什么等于cosθ，如下图所示，红色线段就是|b|*cosθ = cosθ
几何意义
点积的几何意义很重要，因为点积几乎应用到了图形学的各个方面。其中一个几何意义就是投影。
投影是什么意思？加入现在有一个光源，它发出的光线是垂直于单位矢量a方向的，那么矢量b在a方向上的投影就是b在a方向上的影子。
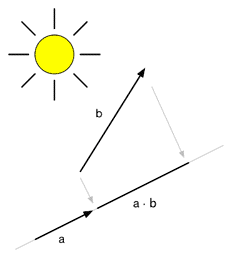
投影结果的正负号与a和b的方向有关：当它们的方向相反（夹角大于90°）时，结果小于0。当它们的方向相同（夹角小于90°）时，结果大于0。当它们互相垂直（夹角为90°）时，结果等于0。这一点利用公式2也可以看出来，结果的正负取决于cosθ。
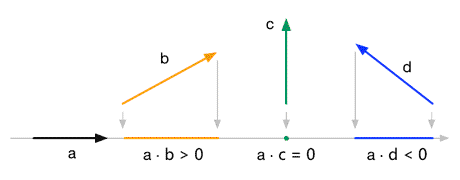
那么如果a（前面所说的投影都要求a是单位矢量）不是一个单位矢量会如何呢，很简单，任何两个矢量的点积a·b等同于b在a方向上的投影，再乘以a的模。
点积的性质
- 点积满足交换律，即 a·b = b·a
点积可以结合标量乘法
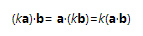
点积可结合矢量加法/减法
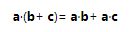
- 一个矢量和本身进行点积的结果，是该矢量模的平方。这意味着，如果我们需要比较两个矢量模的大小，可以直接计算两个矢量与自身的点积来进行比较。省去了开平方的操作。
- 点积的符号可以让我们知道两个矢量的方向关系
利用公式2，可以计算两个矢量之间的夹角
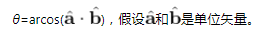
矢量的叉积
与点积不同的是，矢量叉积的结果仍是一个矢量，而非标量。
公式
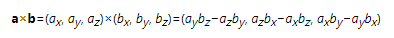
需要注意的是叉积不满足交换律，但是满足反交换律。即a×b = -(b×a)
几何意义
对两个矢量进行叉积的结果会得到一个同时垂直于这两个矢量的新矢量
叉积最常见的一个应用就是计算得到垂直于一个平面，三角形的矢量。
新矢量的模等于a和b的模的乘积再乘以它们之间夹角的正弦值，计算公式如下：
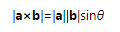
这和平行四边形的面积计算公式是一样的，即底乘以高，可以认为新矢量的模是两个矢量围成的四边形的面积。
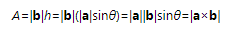
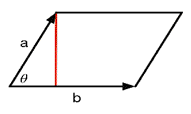
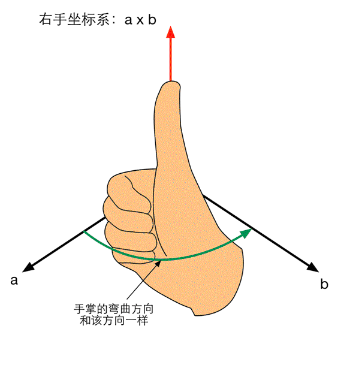
新矢量的方向，就是和两个矢量垂直的方向，但实际上我们有两个方向可以选择。具体如何选择，需要依据左手坐标系或右手坐标系来判断。
以右手坐标系为例，使用右手法则来判断。先把手心放在a和b的尾的交点处，然后张开手掌让手掌的方向和a的方向重合，再弯曲四指让它们向b的方向靠拢，最后伸出大拇指，大拇指的指向就是a×b的方向。对于左手坐标系使用左手法则来判断也是类似的。
