回归(Regression)
KeyWords
- Linear Model(线性模型)
- Loss Function(损失函数)
- Gradient Descent(梯度下降)
- Generalization(泛化)
- Overfitting(过拟合)
- Regularization(正则化)
Regression可以做什么
如果说机器学习(Meachine Learning)要做的事情是要找一个Function,那么Regression要做的事情就是我们要找的那个Function是一个数值(Scalar)。如果我们要找的Function是一个数值,那么这种任务就叫做Regression。
那么Regression应用有哪些呢?
- 股票市场的预测
例如:找一个Function,Input是过去十年的股票市场的变动情况或资讯,Output是明天道琼工业指数的数值。

- 无人驾驶
例如:找一个Function,Input是无人车上的各个传感器(Sensor)所感应到的数据,Output是方向盘的角度。

- 推荐系统
例如:找一个Function,Input是某一个使用者A的特性和购买记录以及商品B的特性,Output是使用者A购买商品B的可能性
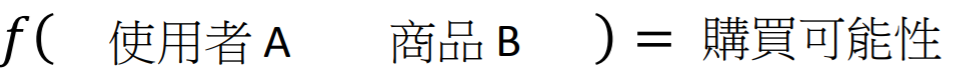
Regression应用举例
目标:预测进化后的Pokemon精灵的攻击力(CP值)
Input:Pokemon精灵的种种特性 (例如:当前Pokemon精灵进化前的CP值 、物种 、HP值 、重量 、高度 …)
Output:Pokemon精灵进化后的攻击力(CP值)
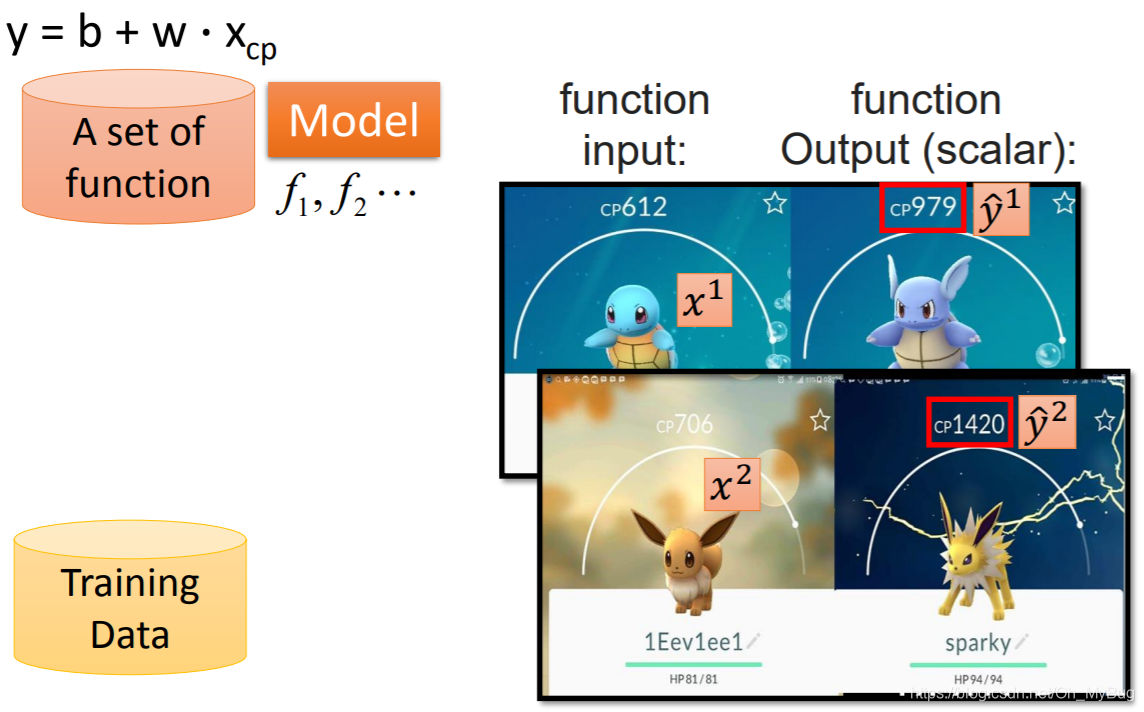
Step 1:Model—Linear Model(线性模型)

第一步是找一个模型(Model),所谓的模型,其实就是一个Function Set。这里的模型我们可以取作 (假设我们相信Pokemon精灵进化后的CP值与进化前的CP值有很大的关系)。
为什么说模型是一个Function Set呢?
这是因为当前我们的模型已经确认是 ,而 和 就是模型的参数(Parameters),如果我们将一组特定的 和 值代入我们的模型 ,那么就可以确定一个Function。因为我们的 和 可以取任何值,所以这些Function就构成了一个Function Set。因此,模型其实就是一个Function Set。而机器要做的,就是在这些无穷多的Function构成的Function Set中,挑选出一个最合适的Function。
这里所确定的模型 ,我们称之为Linear Model(线性模型)
其中
,
(权重),
(偏置)
这里可能会问,明明有这么多特征( , )可以用,为什么只选择 呢?
这取决于你的Domain Knowledge(对一些领域的了解),模型的特征并不是越多越好的,这会让计算变得复杂,所以我们在挑选特征的时候往往会选择认为和预测的目标关系比较大的特征。这里我们认为Pokemon精灵进化后的CP值与进化前的CP值有很大的关系,而对其他的信息缺少一定的认知或者认为关系很小。
Step 2:Goodness of Function
我们已经确定了一个Model,现在我们要做的是确定Funtion Set中的Function对预测结果是好是坏,并把好的Function挑选出来。
首先,我们需要收集一些Training Data(训练数据),Training Data内容包括:
其中,
代表第
只Pokemon精灵所包含的特征(目前只有进化前的CP值
),
代表第
只Pokemon精灵进化后的实际CP值。
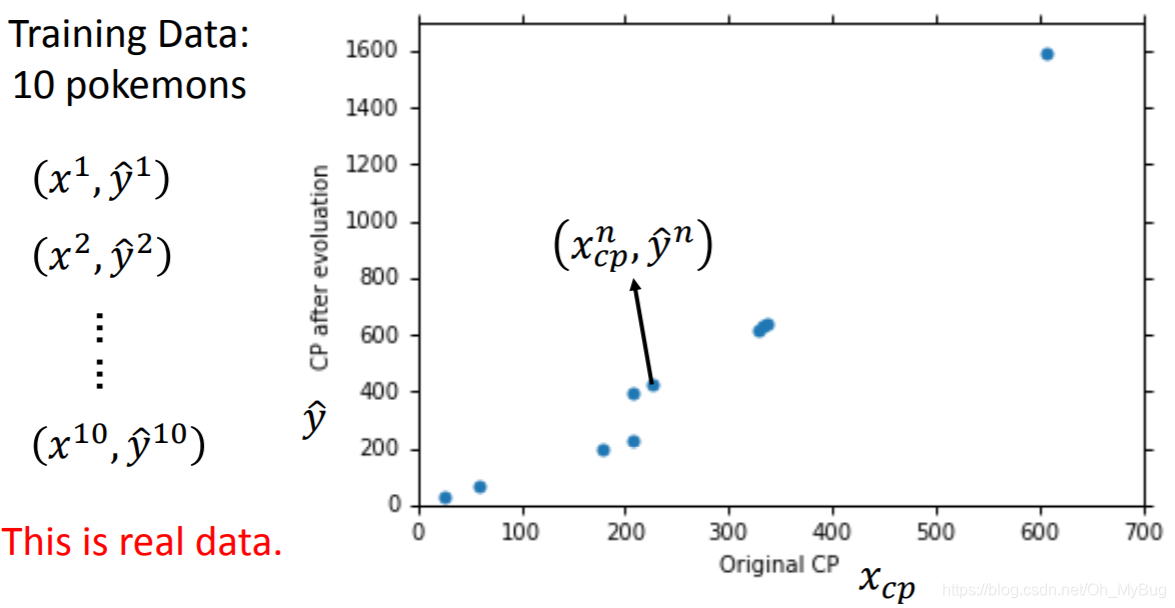
现在我们有十个关于Pokemon精灵的真实数据(n=10),我们将它作为我们的训练数据,并作图(横坐标代表Pokemon精灵进化前的CP值,纵坐标代表Pokemon进化后的CP值)。
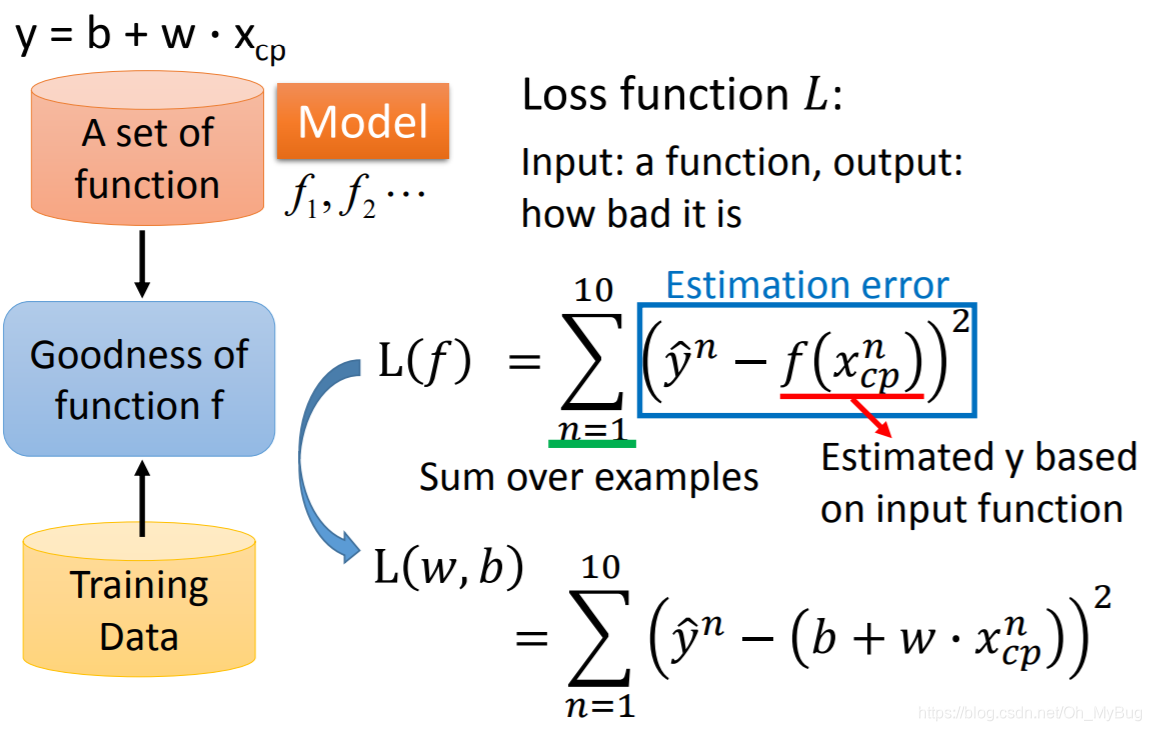
有了这些Data以后,我们就可以来衡量Function Set中的Function中的好坏。为了衡量这些Function中的好坏,我们需要引入一个新的Function—Loss Function。Loss Function的Input是Model(Function Set)里的一个Function,Output是这个Function的好坏。
这里Loss Function定义为:
其中,
是Function Set中的Function基于输入Pokemon精灵进化前的CP值预测出来的Pokemon精灵进化后的CP值
。
因为
,所以Loss Function可以写作:
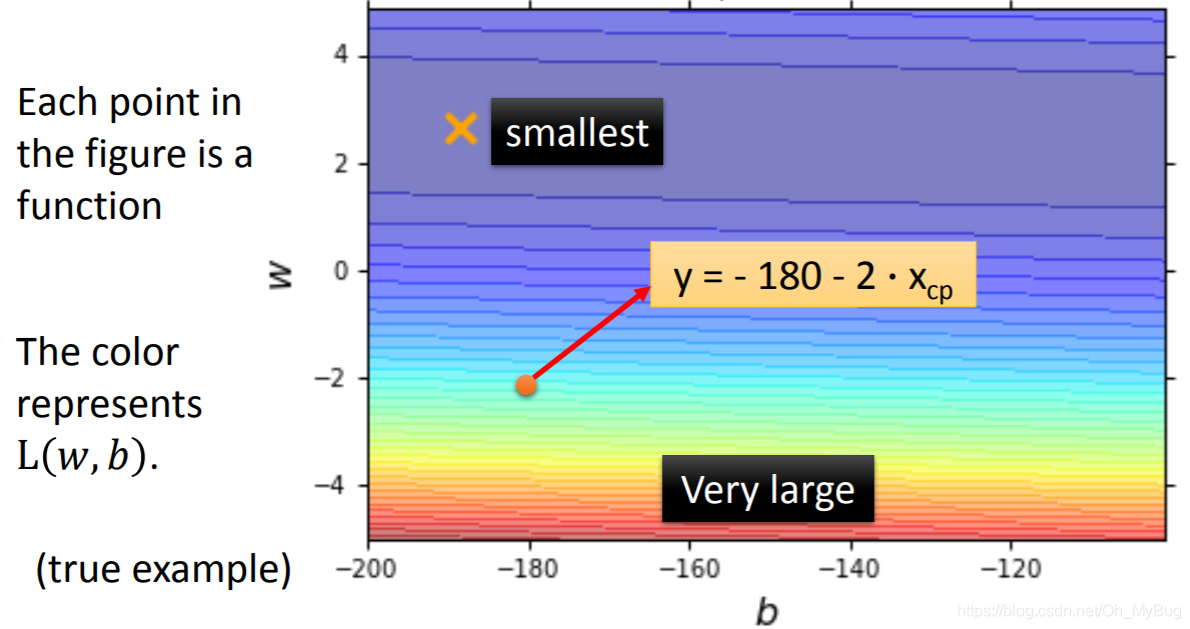
将Loss Function进行可视化(穷举在一定范围内的所有 和 ),如上图,横坐标代表 值,纵坐标代表 ,则图中的每个点代表一个Fuction,而颜色代表Loss Function在特定 和 下的值 ,越蓝代表这个点所对应的Function的 越小,对应的Function也越好;反之,越红代表这个点所对应的Function的 越大,对应的Function也越坏。
在实际中,我们不能限定 和 的范围,因此我们不能用穷举的方式找到最小的 。因此,我们要用其他的办法来实现我们的目标—就是找到那个 最小的点对应的 和 值。
Step3:Best Function
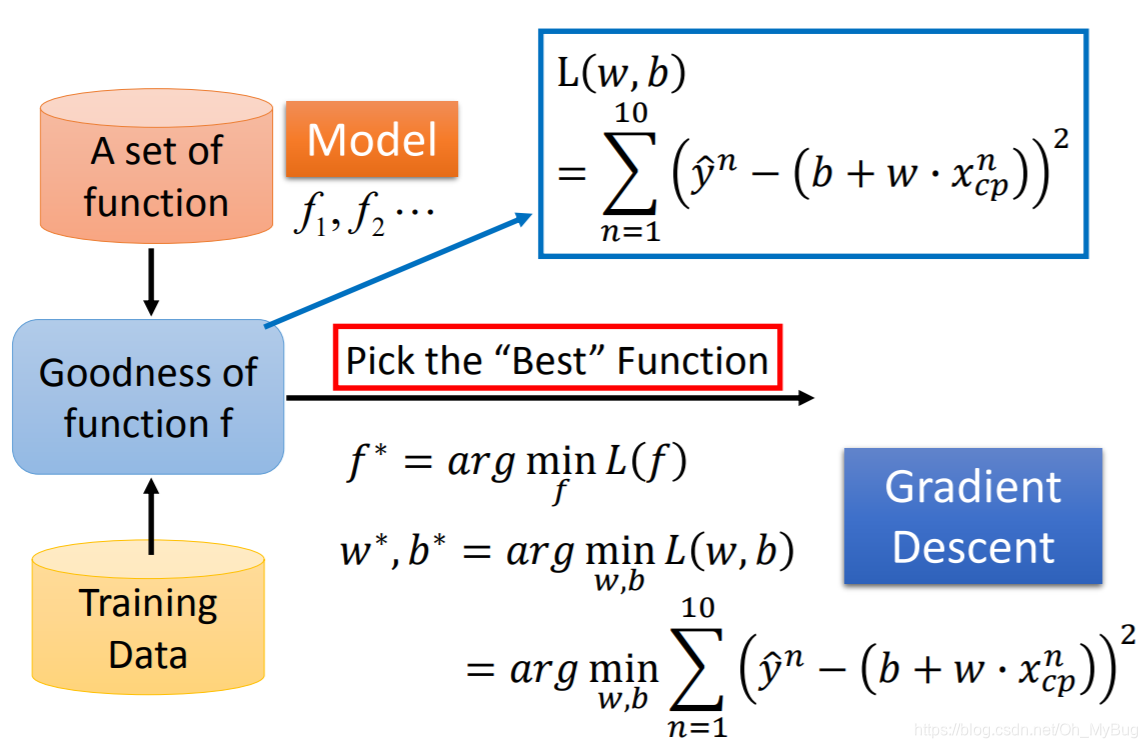
第三步骤就是要找一个最好的Function,这实际上是一个Optimization Problem(最优化问题),也就是说,我们要找一个Function,可以让 的值最小,我们定义这样的Function为:
也可以写作:
接下来我们要做的事情就是求解这个Optimization Problem(最优化问题),而求解的方式就是运用Gradient Descent(梯度下降)。
注意:只要Loss Function对输入的参数( 和 )是可微分的,那么就可以用Gradient Descent(梯度下降)。
Step3:Gradient Descent(梯度下降)
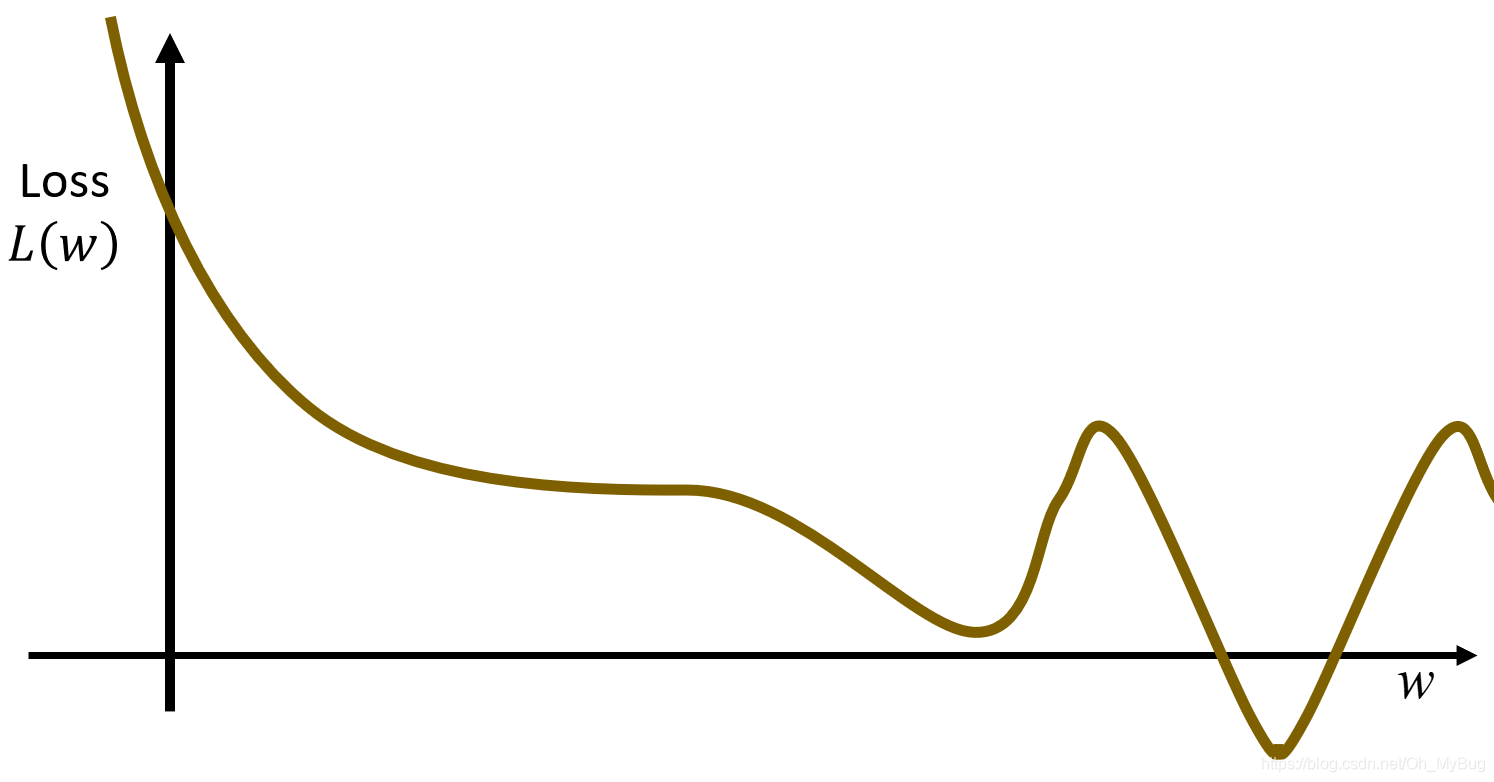
现在我们先考虑一个简单的情况,即只有一个参数
:
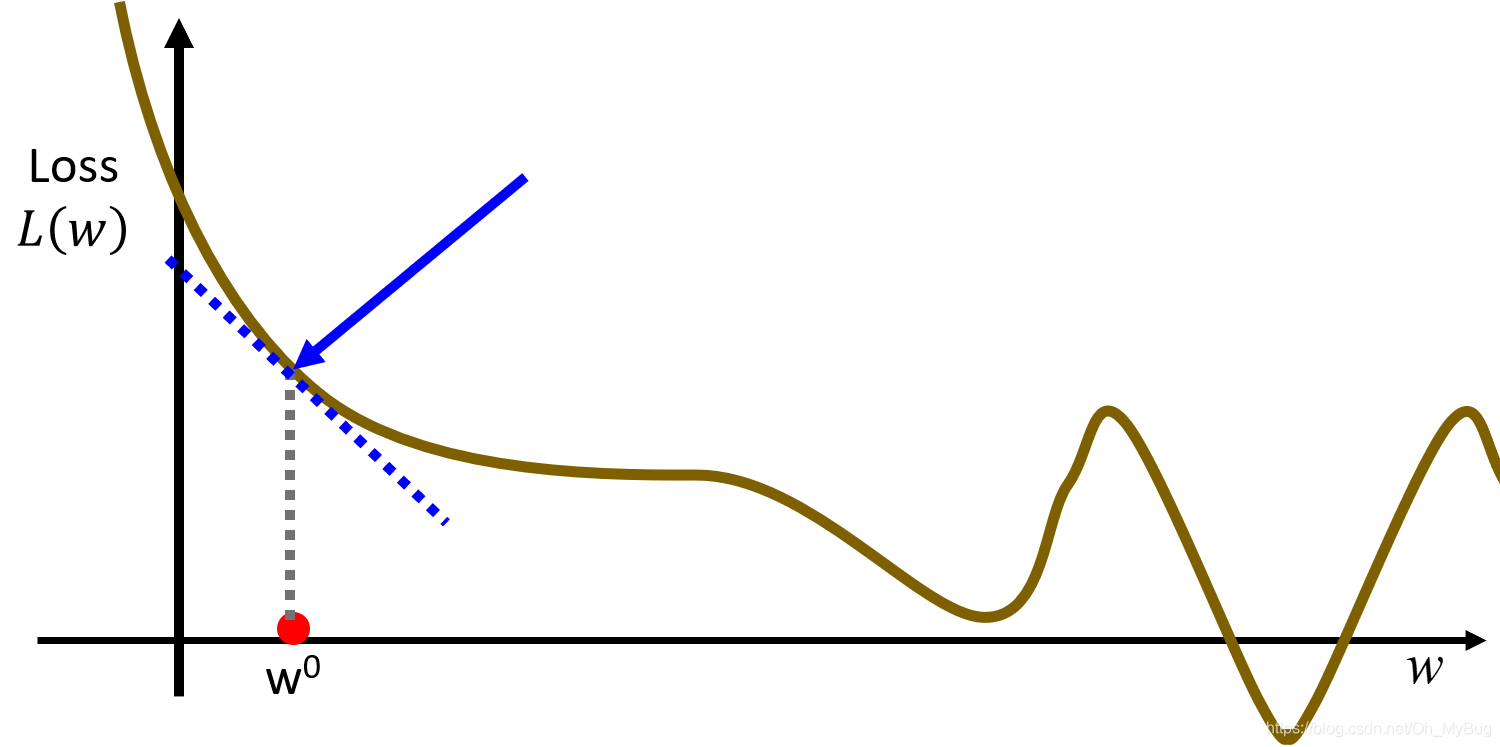
可以把不同的 对 的变化画出来(如下图,横坐标代表 ,纵坐标代表 )。
Gradient Descent(梯度下降)具体步骤:
- 随机初始化
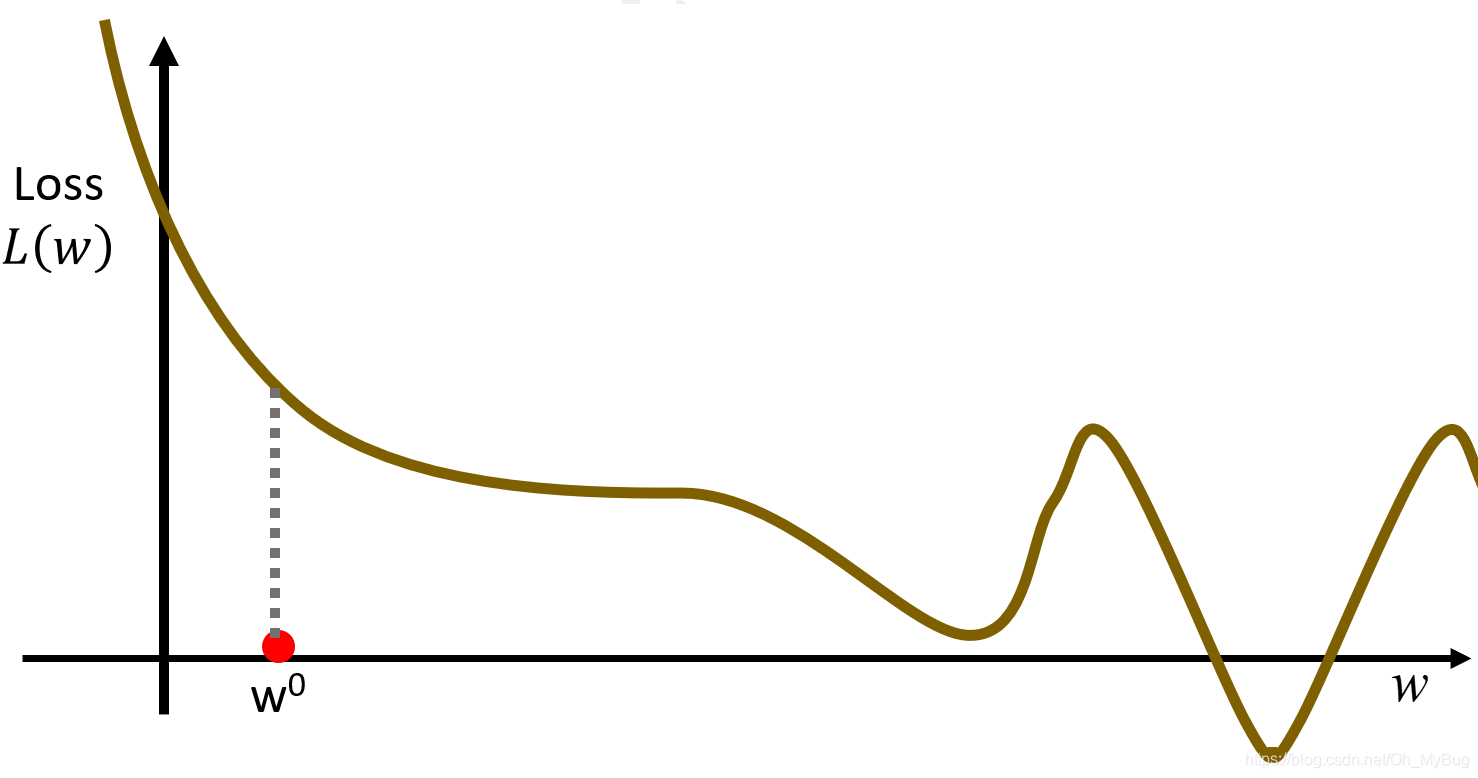
- 计算微分 (在二维空间上,微分即为函数对应点的导数)。假设导数是负的,则意味着函数在递减,这是需要将参数 向右移动,使得 变小;反之,假设导数是正的,则意味着函数在递曾,这是需要将参数 向左移动,使得 变小
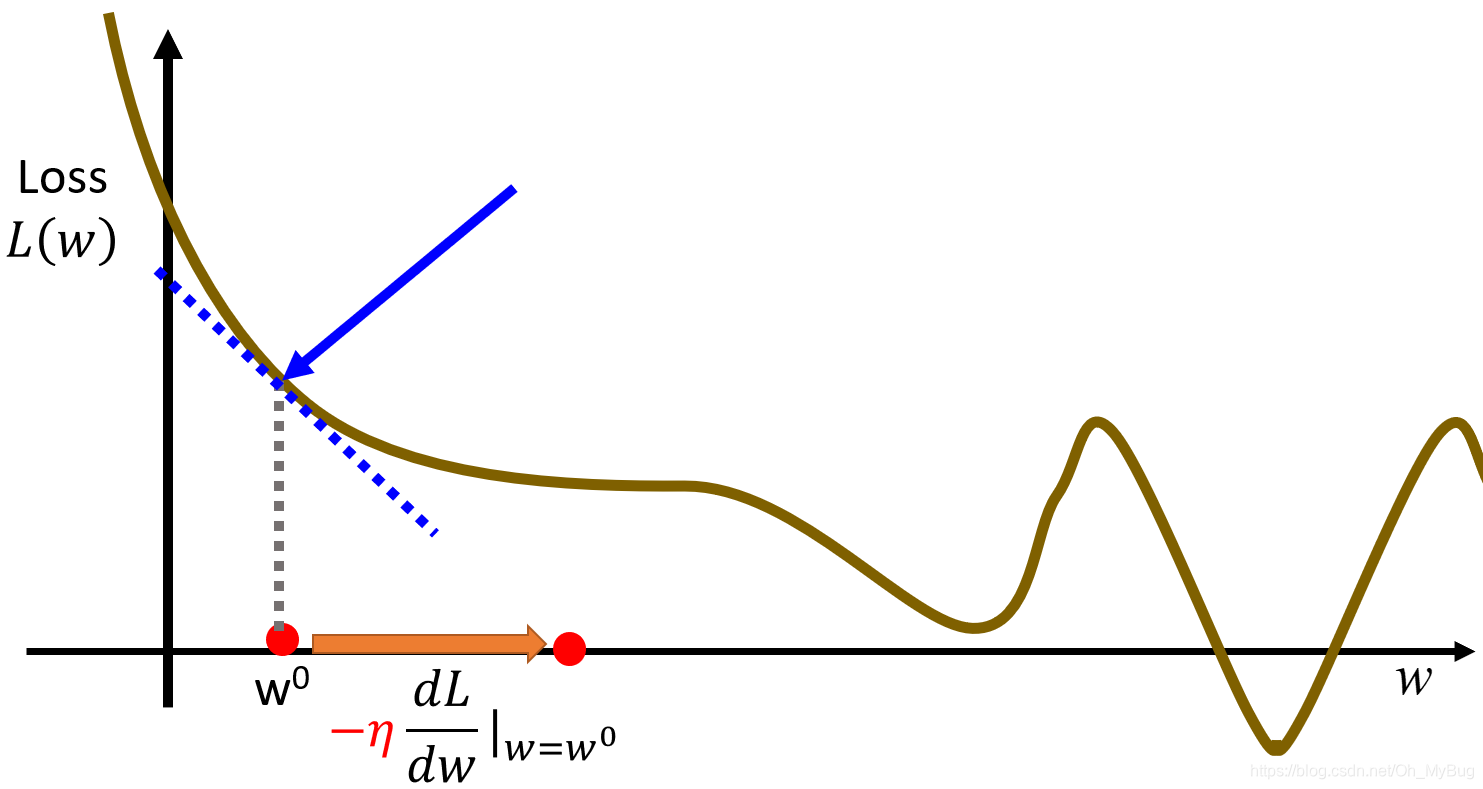
- 更新
:
其中, 代表learning rate(学习率),它决定了你学习的速度有多快。 不能太大也不能太小
- 重新开始第2步,计算微分 ,直到计算出来的微分为0
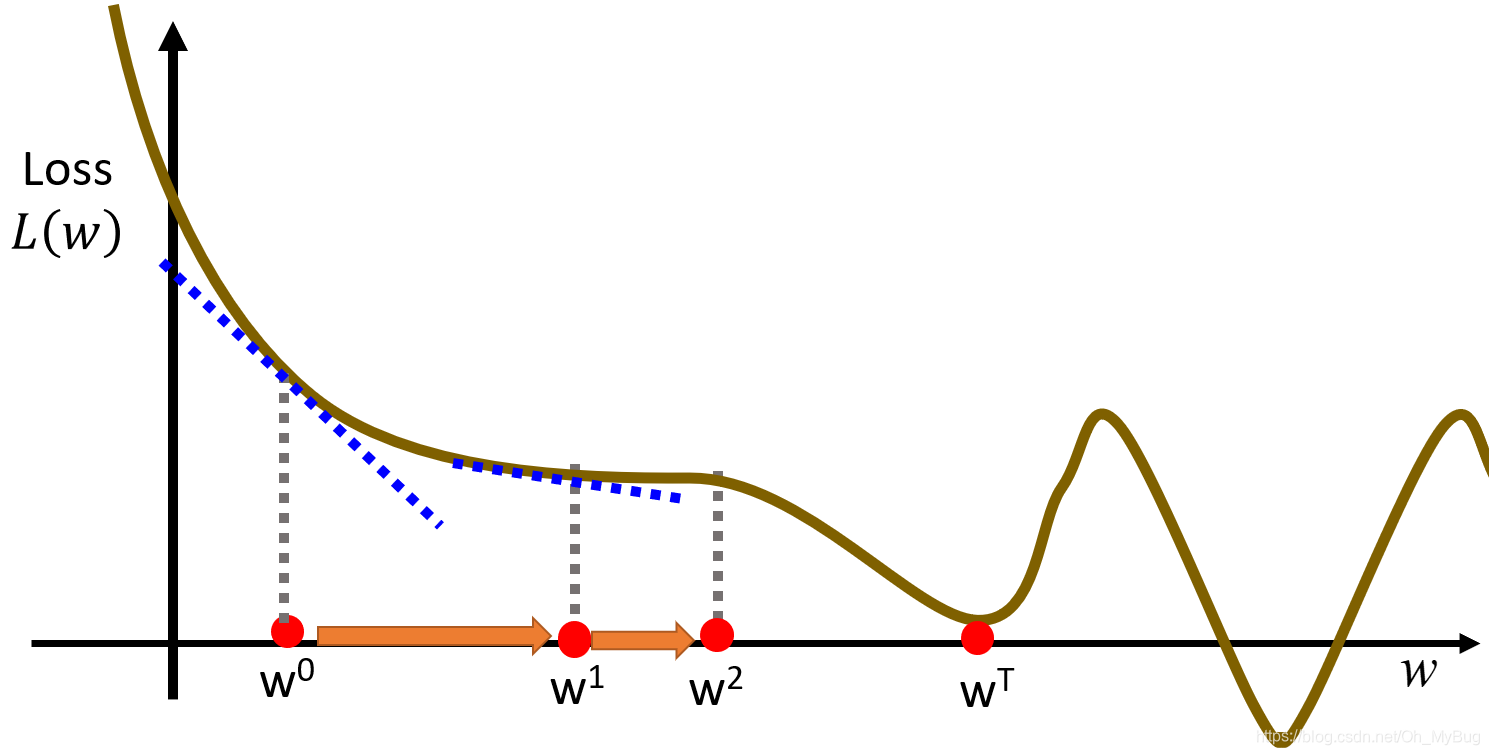
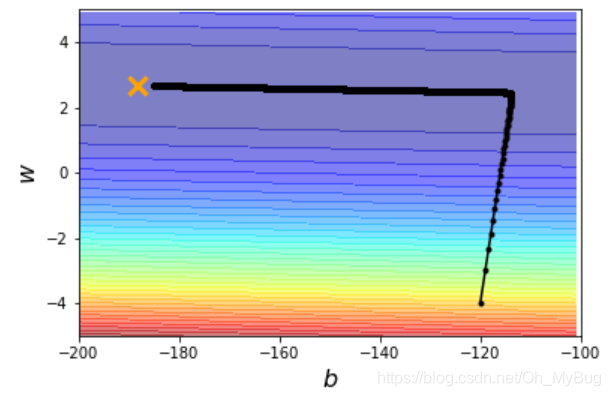
可以容易的发现,最终更新的 可能会陷入Local minima(局部最小)点,所以Gradient Descent(梯度下降)不一定能保证 可以得到Global minima(全局最小),这与随机初始值有关。
注意:是否存在Local minima(局部最小)点与自身函数(在这里是Loss Function)有关。
现在我们考虑有两个参数
和
的情况:
可以把不同的 和 对 的变化画出来(如下图,横坐标代表 ,纵坐标代表 ,颜色代表 的大小)。
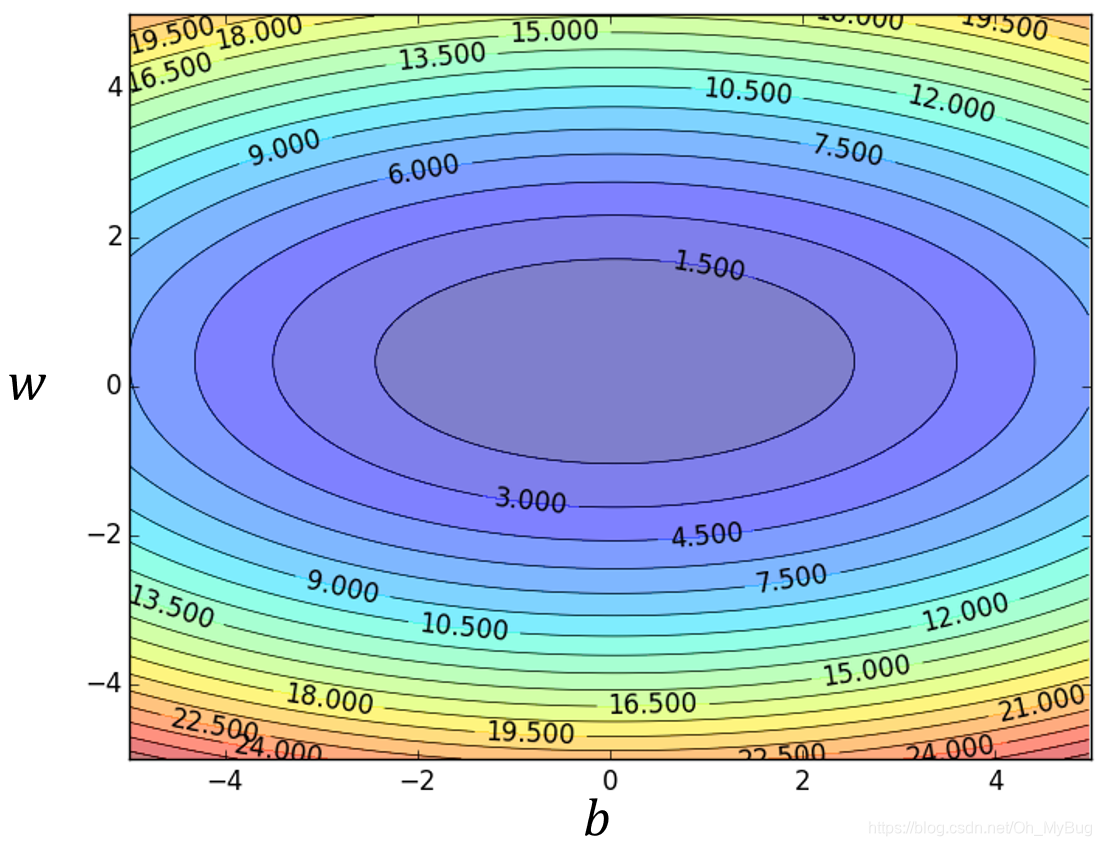
Gradient Descent(梯度下降)具体步骤:
- 随机初始化 和
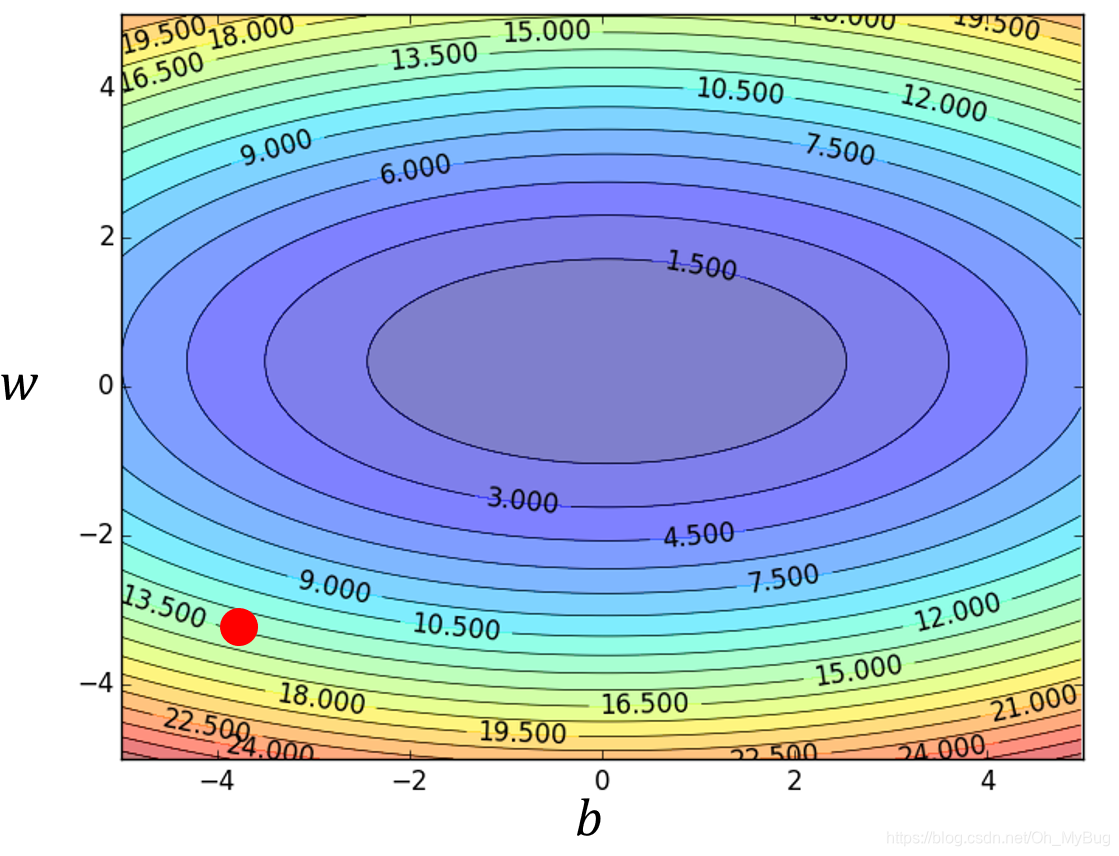
- 分别计算微分
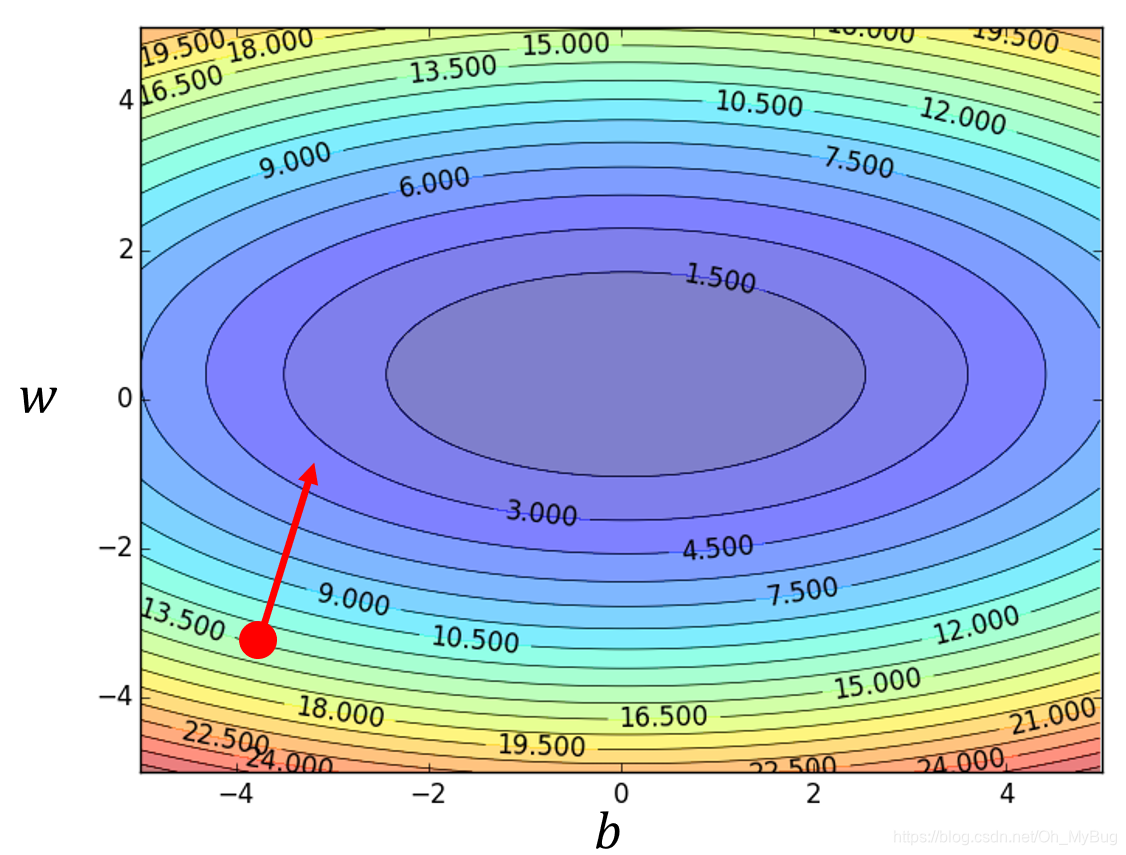
- 更新
和
:
而由 和 构成Gradient(梯度)为:
同时Gradient(梯度)的方向指向当前点 所在等高线的法线方向,而Gradient(梯度)的反方向 就是Gradient(梯度)下降的方向。
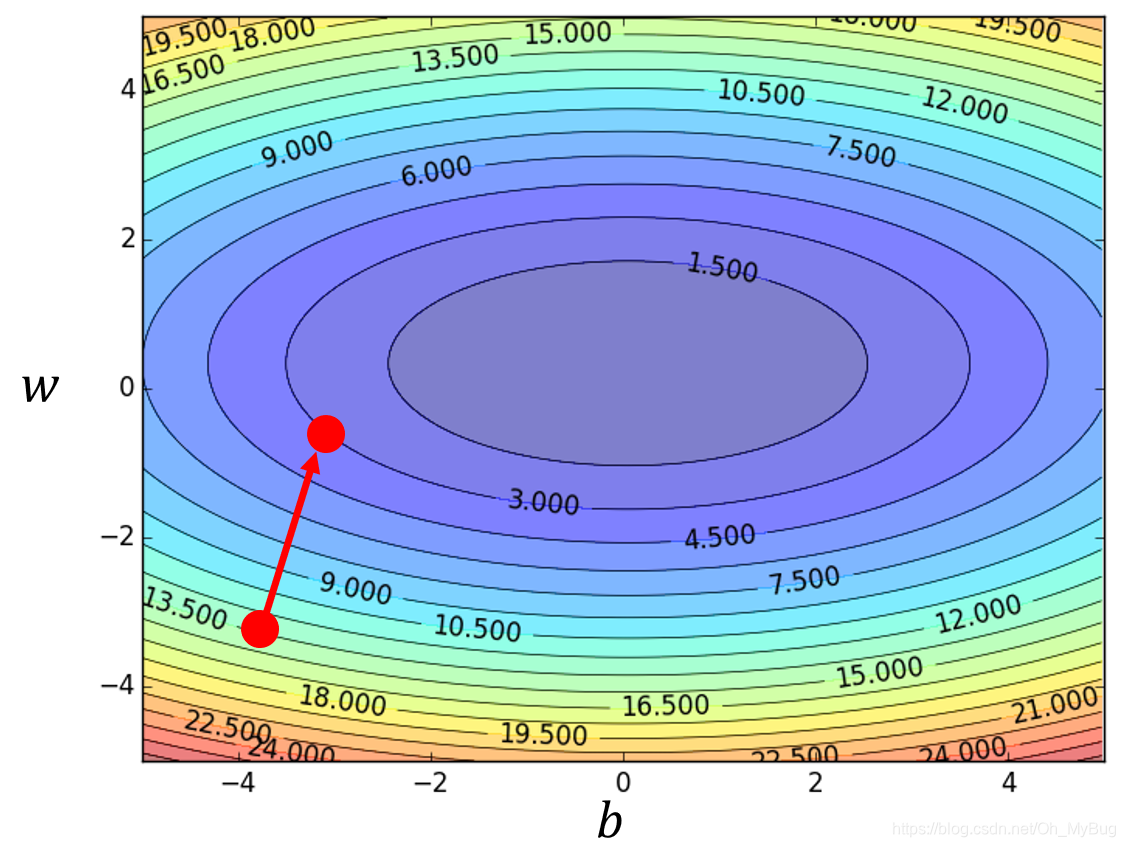
- 重新开始第2步,计算微分 ,直到计算出来的微分均为0
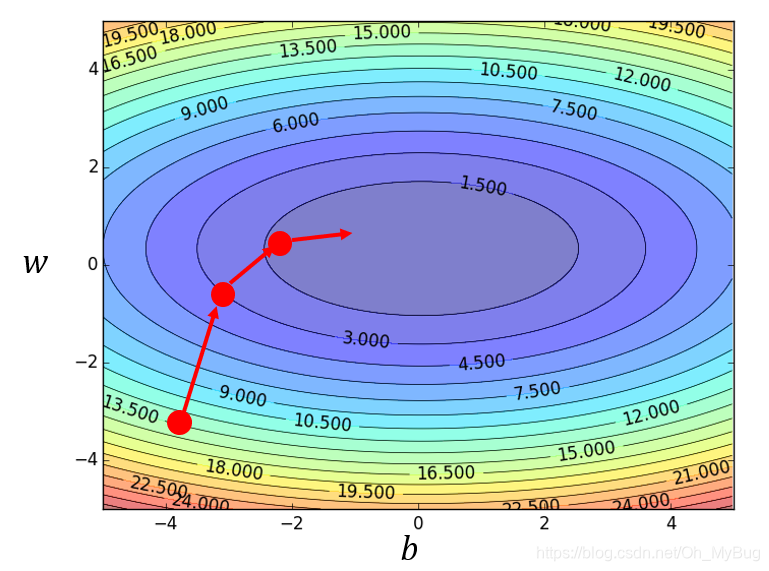
那么到这里,可能有的人就会问了,Gradient Descent(梯度下降)有没有什么问题或者时缺陷呢?
答案是有的。
Gradient Descent(梯度下降)的问题:
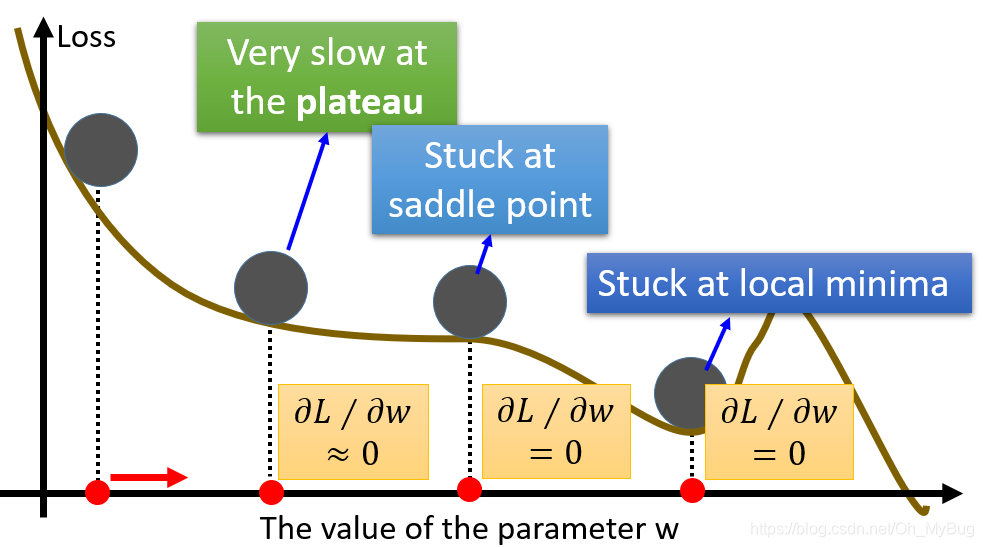
- Stuck at the Local Minima(局部最小)
因为Local Minima所在点的微分(梯度)为0,所以当参数走到Local Minima时参数更新会停止。
- Stuck at the Saddle Point(鞍点)
什么是Saddle Point(鞍点)?简单地说,鞍点是微分(梯度)是0,但是却不是极值的点。所以当参数走到Saddle Point时参数更新也会停止。
- Very slow at the Plateau(一些特殊的地形,如大面积的平坦区域)
在实际中,我们不会真的让Gradient(梯度)等于0的时候(概率很小)才停止参数更新,而是会设置一个很小的阈值,当Gradient(梯度)到达这个阈值的时
候就停止参数的更新。但是存在一些平坦区域,虽然微分不为0,但却很小,其梯度下降的路程非常的远,需要走很多步才能走出这一片平台区域,但是此时的Gradient(梯度)却到达这个阈值,这时候参数更新也会停止。
但是在做Linear Regression(线性回归)的时候,其实不需要太担心这些问题,因为Linear Regression(线性回归)的Loss Function(二次函数)是一个类似"碗"的形状(只有一个极值点),所以你从碗的任何一个位置开始都会滚到碗的中间。
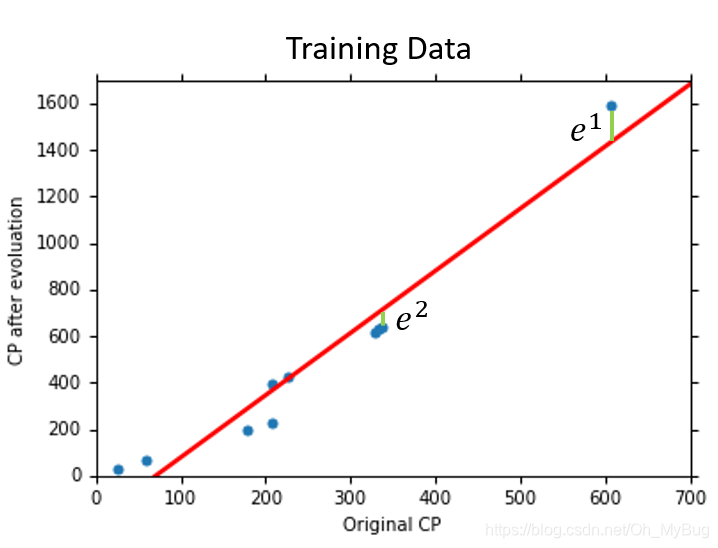
接下里我们就来看一下实际的结果: ,那么就可以算出在Training Data(训练数据)中的Error(误差)是
但是,我们在意的并不是训练数据的Pokemon进化后的CP值是多少,因为我们已经有答案了,而我们真正在意的是这个训练出来的Function对我们从来没有见过的Pokemon精灵的预测能力是如何呢? 即泛化(Generalization)能力——通俗来讲就是指学习到的模型对未知数据的预测能力。在实际情况中,我们通常通过测试误差来评价学习方法的泛化能力。如果在不考虑数据量不足的情况下出现模型的泛化能力差,那么其原因基本为对损失函数的优化没有达到全局最优。
这里我们引入另外十只Pokemon精灵作为Testing Data(测试数据),将Pokemon精灵进化前的CP值代入模型中得到Pokemon精灵进化后的CP值的预测值,并计算出在Training Data(训练数据)中的Error(误差)是 ,略大于Training Data(训练数据)中的Error(误差)是很合理的,因为最好的Function是根据Training Data找出来的,模型从来没有接触过Testing Data。
那我们能不能做得更好呢?
在我们的想象里面,Pokemon精灵进化前的CP值和进化后的CP值是一条直线的关系,但是从这个图上,显然可能不是一条直线的关系,也许是更复杂的关系。
例如Pokemon精灵进化后的CP值和进化前的CP值是不是存在二次的关系?那我们就试一下!
即:
最终结果为:
注意: 虽然是二次曲线,但它实际上是一个Linear Model(线性模型)。这是为什么呢?因为所谓一个Model(模型)是不是Linear Model(线性模型)是指参数对Model(模型)的Output(输出)是不是Linear(线性的)。显然,你可以把 看作是一个feature(特征),把 看作是第二个feature(特征),所以它仍然是一个Linear Model(线性模型)。
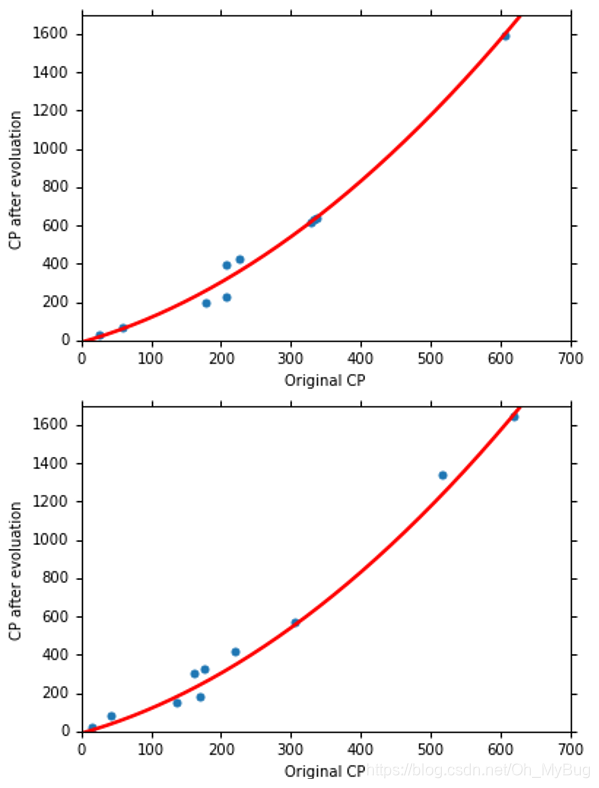
那能不能做得更好呢?会不会是三次曲线呢?那我们就试一下!
即:
最终结果为:
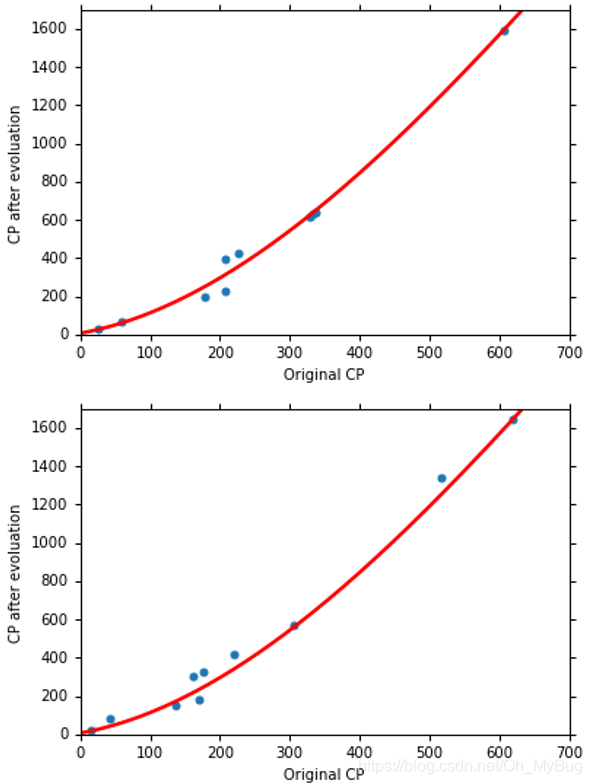
那能不能做得更好呢?会不会是四次曲线呢?那我们就试一下!
即:
最终结果为:
显然,Testing Data的结果变差了!
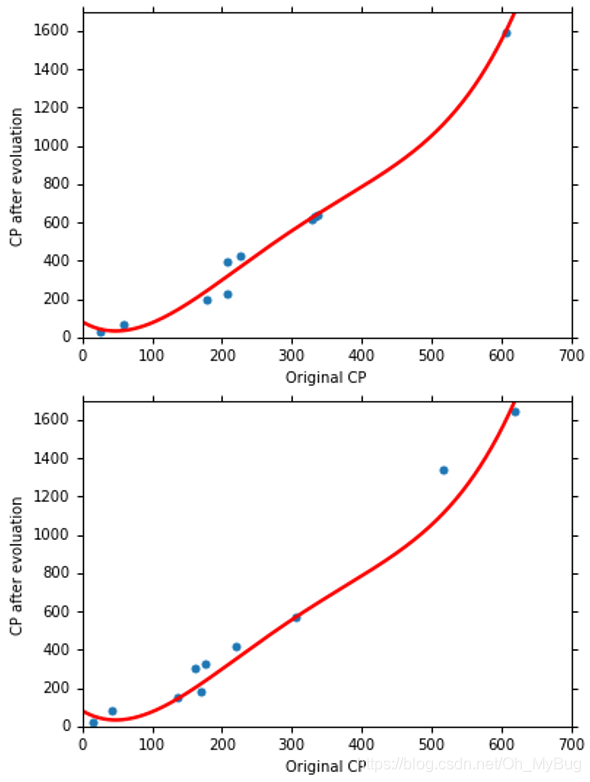
我们再试一下五次曲线!
即:
最终结果为:
显然,Testing Data的结果变得非常差!而且由图可以看到,当Pokemon精灵进化前CP值在500左右时,预测出来的结果变成了负值,这显然是不合理的!
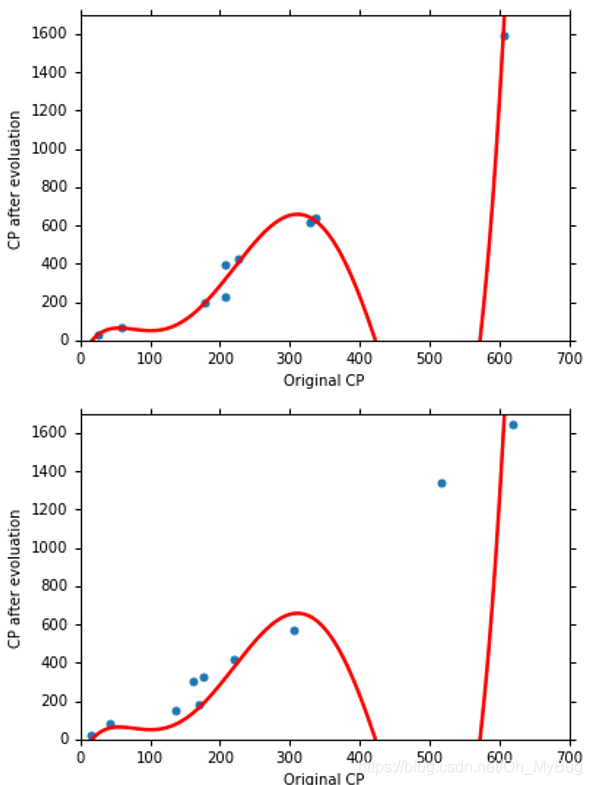
那为什么会这样子呢?我们来分析一下。
- 对于Training Data(训练数据):
我们知道,对于每个Model来说其实都是一个Function Set,当Model越复杂时,Function Set越大且包含了简单Model的Function Set,比如三次Model的Function Set其实是四次Model的Function Set( )的一个子集合。所以,当Model越复杂时,我们能在更多的Function中挑选最好的Function,从而使得Training Data的Error越低。
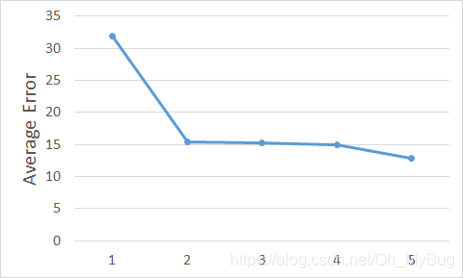
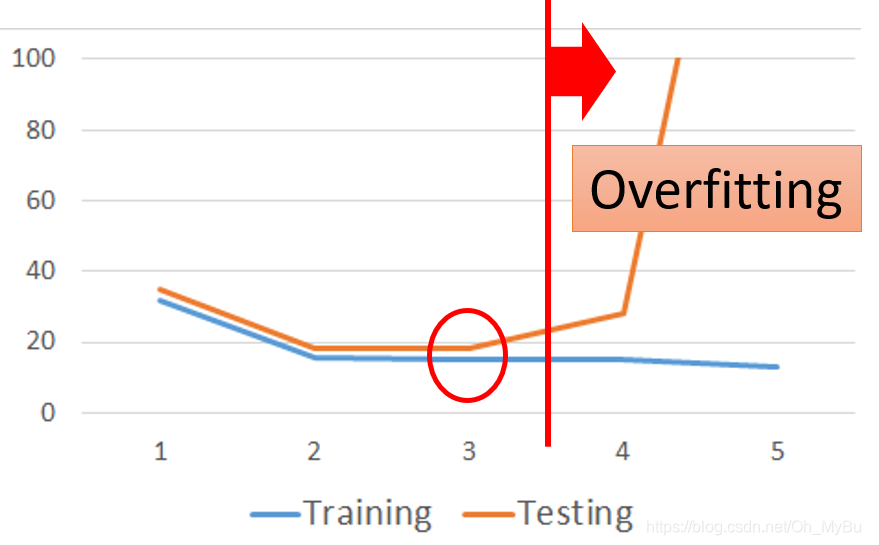
- 对于Testing Data(测试数据):
我们发现,三次Model的Performance(效果)是最好的。当Model越复杂时,Error就会突然爆炸,所以一个复杂的Model,并不一定总会在Testing Data(测试数据)给我们一个好的Performance。这是Overfitting(过拟合)现象。Overfitting(过拟合)的根本原因是特征维度过多,模型假设过于复杂,参数过多,训练数据过少,噪声过多,导致拟合的函数完美的预测训练集,但对新数据的测试集预测结果差。过度的拟合了训练数据,而没有考虑到Generalization(泛化)能力。
那要怎么解决Overfitting(过拟合)呢?其中一个方法就是收集更多的Data(如下图)。
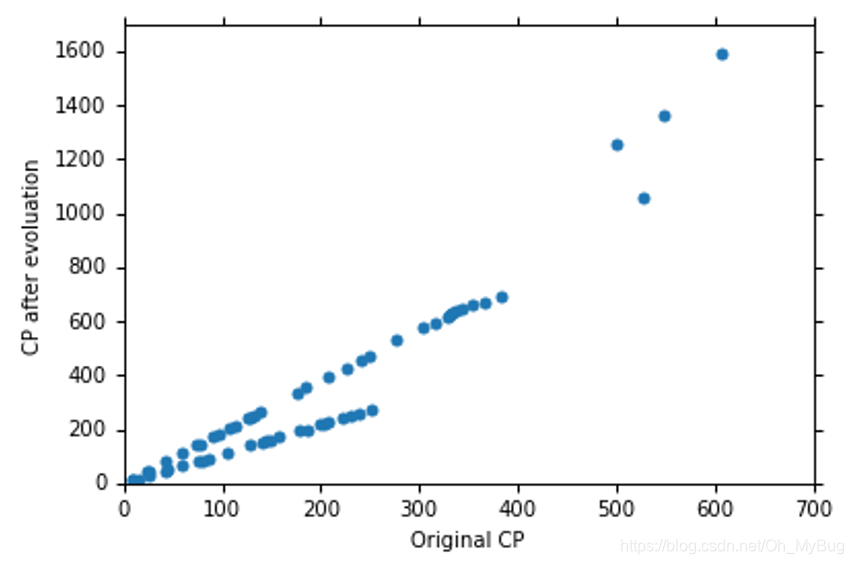
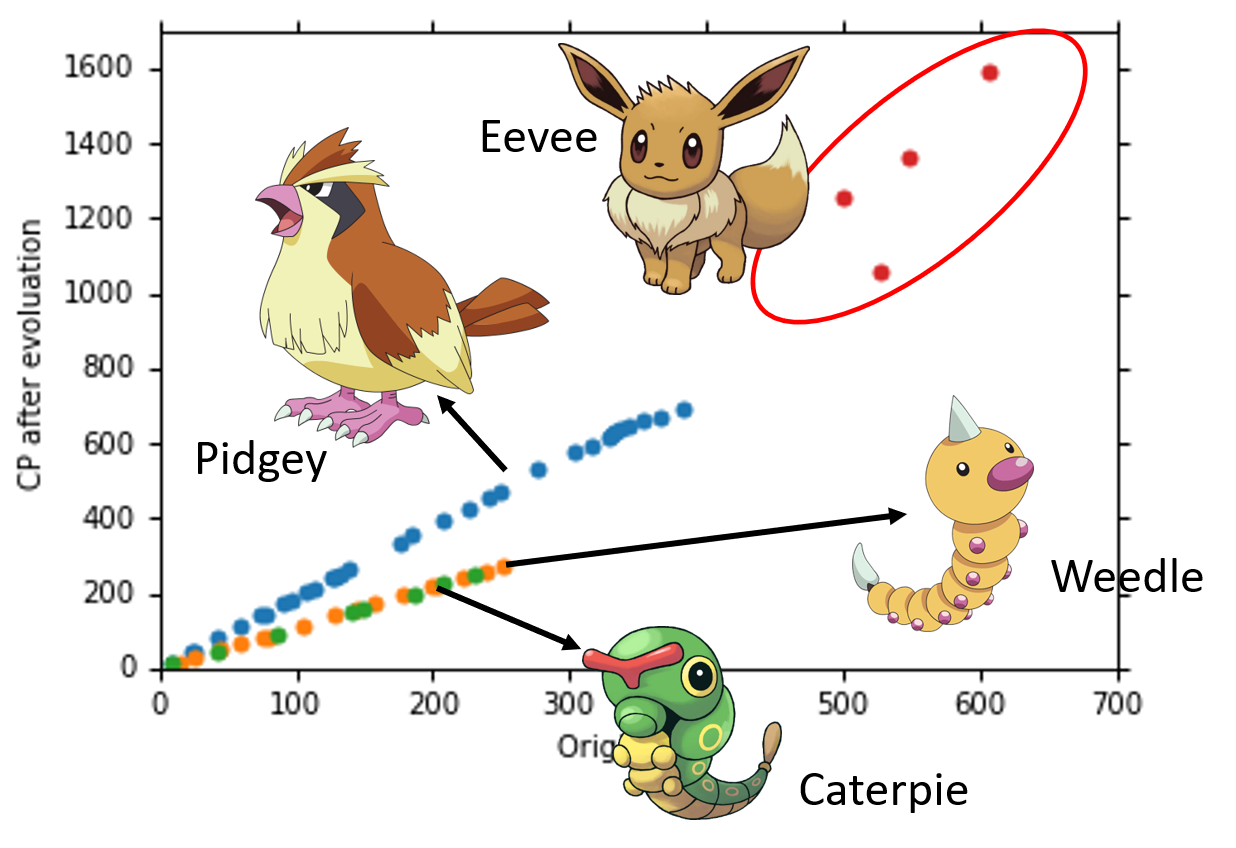
从图中可以发现,Pokemon精灵进化前的CP值相同,但是进化后的CP值却存在很大的差异,所以可以说,有另外一个我们没有考虑到的因素它影响了Pokemon进化后的CP值。当把不同品种的Pokemon精灵用不同颜色画出来的话,你就会发现其实是Pokemon精灵的种类影响了进化后的CP值。因此,我们需要把Pokemon的种类考虑进Model中。
Back to Step 1:Redesign the Model
首先,我们先设计一个比较复杂的Model(如下图)。

那么上图的Model还是Linear Model吗?
我们把上图的Model换成另一种形式(如下图),它们是等价的。
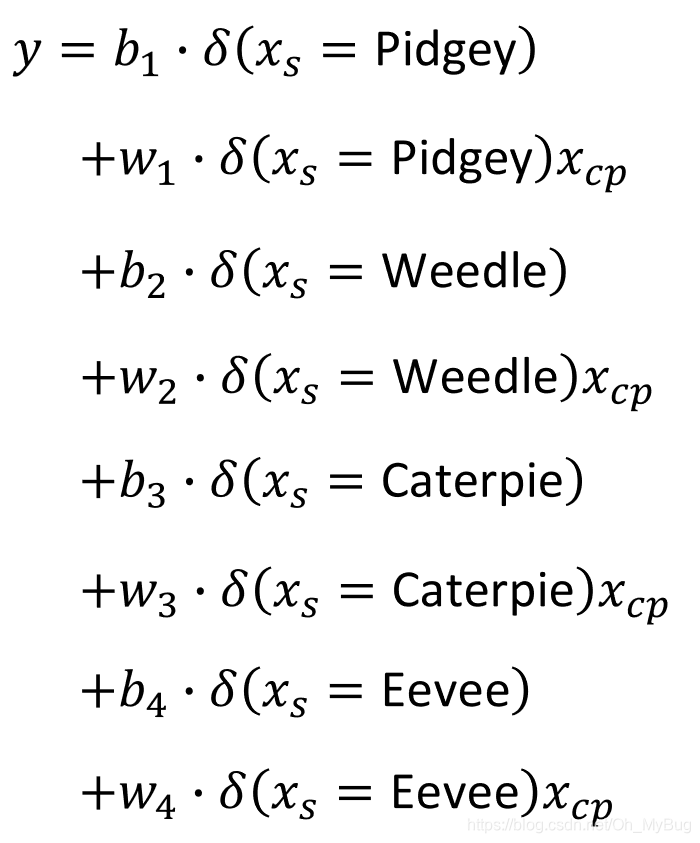
其中,
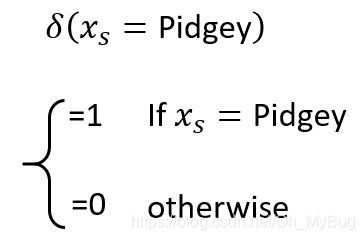
显然,我们可以将 和 所乘的对象当作feature(特征),所以这个Model仍然是Linear Model。
那么重新设计的Model结果如何呢?
最终结果:
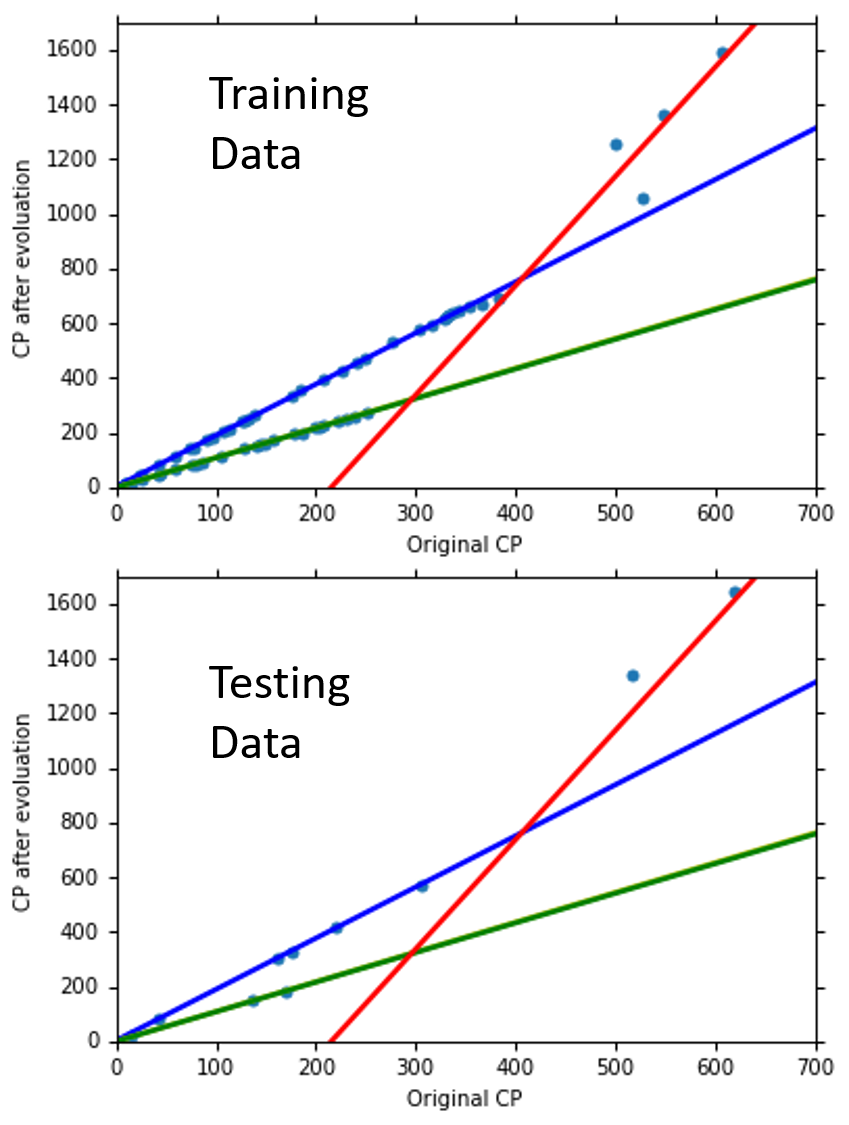
友情提示:图中有两条直线重合了,一共有四条直线。
显然,结果变好了!
那会不会还有其他没有考虑的因素在影响Pokemon进化后的CP值呢(毕竟我们得到 其实也不是0)?会不会二次Model更好呢?
如果没有足够的Domain Knowledge(领域认知)的话,就都尝试一下看看(如下图),显然,结果overfitting(过拟合)。
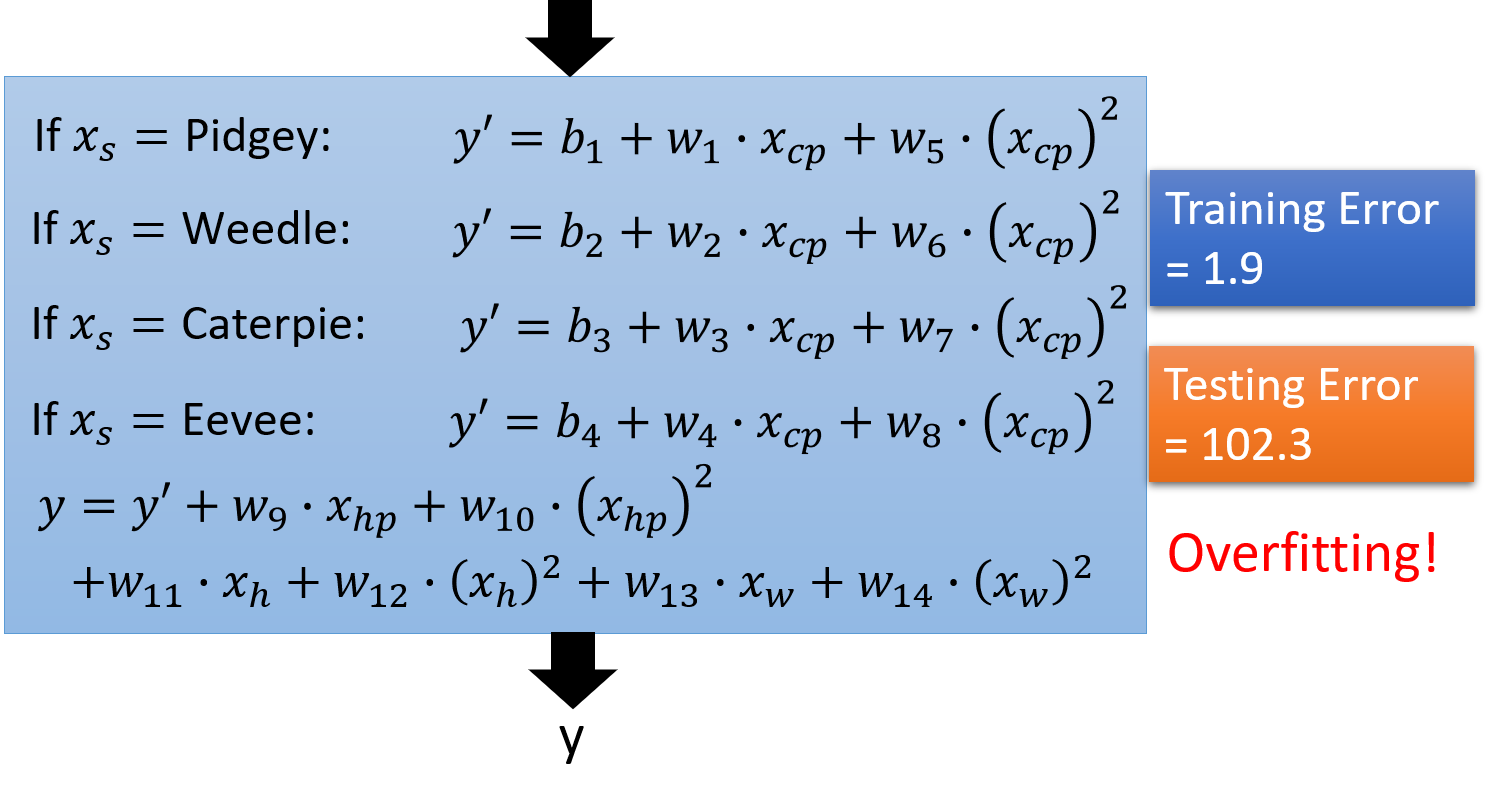
所以接下来,接下来我们要讲的是避免overfitting(过拟合)的另一种方法:Regularization(正则化)。Regularization(正则化)要做的事情就是改变Loss Function。
我们之前用的Loss Function是指在Trainning Data中得到Error最小的Function就是最好的Function,也许这个叙述没有这么的精确,所以我们需要换一个Loss Function。
那么换什么样的Loss Function呢?
原来的Loss Function是观察我们现在预测的Error有多大:
而新的Loss Function除了预测Error有多大之外,还多加了一项
(即
乘于所有参数
的平方和):
可能现在心中充满疑问,为什么要加一项 呢?
因为最好的Function可以让Loss Function最小化,对于之前的Loss Function,只是让Loss Function Error最小。但是,对于新的Loss Function,这不仅可以让新的Loss Function Error最小,而且还可以让
参数变得很小。
很小的Function意味着它是一个比较smooth(平滑)的Function。
什么样的Function才算是平滑的呢?平滑的意思就是对于一个Funtion,输入的变化是小的,那么输出的变化也是小的。如果输入的变化很小,但是输出的变化却很大,那么这个Function就是抖动的。
例如,我们在Function
中加一个变动
,即
如果输出项的
是很小的话,那么整个的输出的变动就会是很小的,那么Function就是平滑的。
我们相信在大多数的状况下smooth(平滑)的Function是正确的Function(也存在少数情况正确的Function抖动得很厉害,此时加Regularization也只是无能为力),所以加Regularization(正则化),在很多情况下都是有用的。
这里展示加了Regularization(正则化)之后的结果(如下图):
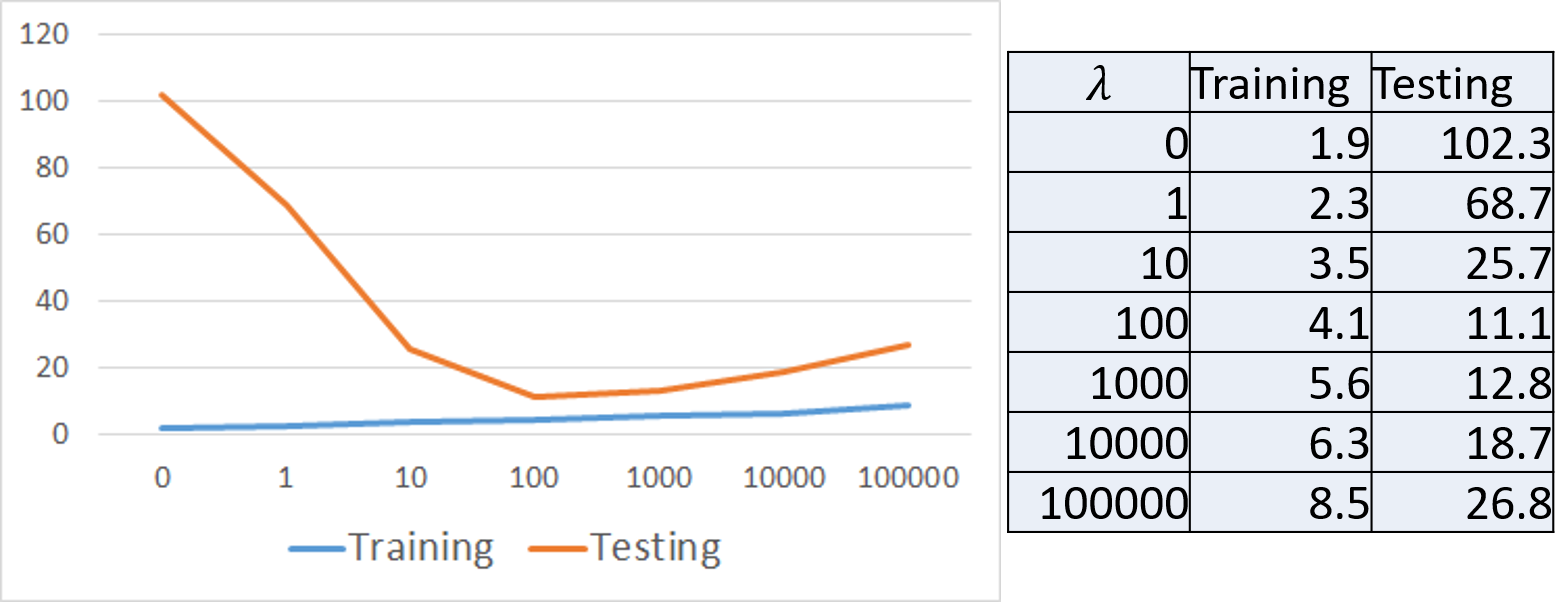
由图可以发现:
- 对于 , 越大, 越大
- 并不是越大越好,需要选择一个最合适的 ,才能得到最好的结果
Conclusion(结论)
- Pokemon精灵进化后的CP值和Pokemon的物种以及进化前的CP值有关系,不可否认也可能有其他的因素影响了Pokemon精灵进化后的CP值
- 最终的Testing Data的Error为11.1
Demo
import numpy as np
import matplotlib.pyplot as plt
x_data = [338.,333.,328.,207.,226.,25.,170.,60.,208.,606.]
y_data = [640.,633.,619.,393.,428.,27.,193.,66.,226.,1591.]
# ydata = b + w * xdata
x = np.arange(-200, -100, 1)
y = np.arange(-5, 5, 0.1)
X, Y = np.meshgrid(x, y)
z = np.zeros((len(x), len(y)))
for i in range(len(x)):
for j in range(len(y)):
b = x[i]
w = y[j]
z[j][i] = 0
for n in range(len(x_data)):
z[j][i] = z[j][i] + (y_data[n] - b - w*x_data[n])**2
z[j][i] = z[j][i] / len(x_data)
b = -120 # initial b
w = -4 # initial w
lr = 1 # learning rate
iteration = 1000000
# store initial value for plotting
b_history = [b]
w_history = [w]
lr_b = 0
lr_w = 0
# iteration
for i in range(iteration):
b_grad = 0.0
w_grad = 0.0
for n in range(len(x_data)):
b_grad = b_grad - 2.0*(y_data[n] - b - w*x_data[n])*1.0
w_grad = w_grad - 2.0*(y_data[n] - b - w*x_data[n])*x_data[n]
# AdaGrad
lr_b = lr_b + b_grad ** 2
lr_w = lr_w + w_grad ** 2
# update parameters
b = b - lr/np.sqrt(lr_b) * b_grad
w = w - lr/np.sqrt(lr_w) * w_grad
# b = b - lr*b_grad
# w = w - lr*w_grad
# store parameters for plotting
b_history.append(b)
w_history.append(w)
# plot the figure
plt.contourf(x, y, z, 50, alpha=0.5, cmap=plt.get_cmap('jet'))
plt.plot([-188.4], [2.67], 'x', ms=12, markeredgewidth=3, color='orange')
plt.plot(b_history, w_history, 'o-', ms=3, lw=1.5, color='black')
plt.xlim(-200, -100)
plt.ylim(-5, 5)
plt.xlabel(r'$b$', fontsize=16)
plt.ylabel(r'$w$', fontsize=16)
plt.show()
以上便是本文全部内容,若有错误,欢迎大家留言指正!谢谢!
