4.5 凸多边形最优三角剖分

1.实验目的

动态规划法解凸多边形最优三角剖分

2.实验内容

2.1 问题描述

(1)凸多边形的三角剖分：将凸多边形分割成互不相交的三角形的弦的集合T。
(2)最优剖分：给定凸多边形P，以及定义在由多边形的边和弦组成的三角形上的权函数w。要求确定该凸多边形的三角剖分，使得该三角剖分中诸三角形上权之和为最小。

2.2 问题分析

• 前置知识
  在凸多边形P的一个三角形部分T中，各弦互不相交，且弦数已达到最大，即P的任一不在T中的弦必与T中某一弦相交。在一个有n个顶点的凸多边形的三角部分中，恰好有n-3条弦和n-2个三角形。
• 动态规划法进行剖分
  1.找出最优解的性质：满足三角形弦值和最小
  2.递归地定义最优值：解该多边形的最优三角划分时，会包含多个子三角形划分，子三角形中面积重叠的部分，需要计算该部分划分三角形后的权值，选取最优值。反复调用，直到多边形是一个可以计算出权值的三角形为止。
  3.自底向上，计算最优值：计算出一个三角形的最优值后，根据最优子结构，步步最优解，根据递归性质，可求得该问题的最优解。

3.实验过程及结果

3.1 数据输入

#定义一个顶点到其他顶点的权
weights=[[0,2,2,3,1,4], 
         [2,0,1,5,2,3], 
         [2,1,0,2,1,4], 
         [3,5,2,0,6,2],
         [1,2,1,6,0,1], 
         [4,3,4,2,1,0]]

weights是一个邻接矩阵，

3.2 实验代码

1. 求权值之和

#定义求三角形权之和的函数
def get_weight(i,j,k):
    weights = [[0, 2, 2, 3, 1, 4], [2, 0, 1, 5, 2, 3], [2, 1, 0, 2, 1, 4], [3, 5, 2, 0, 6, 2], [1, 2, 1, 6, 0, 1],
               [4, 3, 4, 2, 1, 0]]
    if k<n:
        return weights[i][j]+weights[j][k]+weights[k][i]

2. 计算最优决策

def desicion(n,m,s):
    for i in range(1,n):
        m[i][i]=0
        s[i][i]=0
        for r in range(2,n):
            for i in range(1,n-r+1):
                j=i+r-1
                m[i][j]=m[i+1][j]+get_weight(i-1,i,j)
                s[i][j]=i
            for k in range(i+1,j):
                t=m[i][k]+m[k+1][j]+get_weight(i-1,k,j)
                if t<m[i][j]:
                    m[i][j]=t
                    s[i][j]=k
    return m,s

3. 自底向上求取最优值

def MAX(i,j,s):
    if i==j:
        return
        MAX(i, int(s[i][j]), s)
        MAX(int(s[i][j] + 1), j, s)
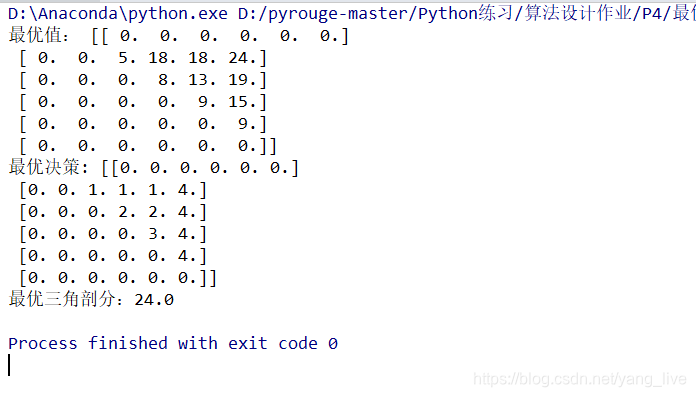
        print('v'+str(i-1)+',v'+str(j)+',v'+str(s[i][j]))
    print('最优三角剖分：'+str(m[1][n-1]))

3.3 实验结果