CRF(条件随机场)详解（内含推导）

和之前讲的HMM模型一样，CRF是一个时序模型，我们先来看一下这个模型的结构吧！

CRF模型结构

看上去和HMM比较相似，但还是有一些不同之处，HMM中我们使用了有向图，在CRF中使用的是无向图，区别是什么呢？

CRF与HMM算法的区别

我们知道HMM中的两大规则1、齐次一阶的马尔科夫假设 2、观测独立假设。我们来分析一下这两个规则合不合理哈：

观测独立性假设：主要是指观测值之间假设是独立的，也就是说给定一组观测值 $x$,其中 $x_1$与其他 $x$之间假设是独立的，这个假设显然在nlp中有一些不合理，比如给定的观测值是一句话，你能说这句话中单词与单词之间是没有联系的吗？当然不是，所以HMM中这种假设是有一定的局限性

齐次一阶的马尔科夫假设：也有一些局限性，意思是每种状态只依赖与前面一种状态，也就是说在很多实际的场景下状态不仅仅只是依赖于前一种。

如上图，我们可以很清楚的看到CRF打破了这两种规则，现在每种状态之间不在是依赖于前一个状态了，现在是一个无向的表示，由于这种无向图也体现出了观测值之间是有联系的，可以从D分布的角度去看这幅图

当然HMM是一种生成模型，而由这幅图可知CRF是一个判别模型，当我们在做下游任务的时候，我们还是经常性的使用判别模型，虽然生成模型也能够完成，但是还是多了一些复杂的操作。

其实还有一些区别，在推导CRF中可以看得出来，比如HMM计算的是一个局部的概率，CRF是计算的全局的概率。

当然推导的过程比较类似，都用到了维特比算法，还有向前向后算法等。

log-linear model

log-linear model其实我认为他不是一个模型，而是一种思想，或者说是一个框架，也就是说对于一个判别任务 $p(y|x.w)$我们需要去设计一个数学模型，首先我们对于目标任务可以设置一个方程来代表： $F(x,y)$来表示 $x$和 $y$之间的某种关系，用 $w$来表示模型的权重我们也经常称为参数

这样我们可以把 $p(y|x,w)$来表示成这样的一种形式：

$p(y|x,w)=\dfrac{e^{\sum_jw_j\cdot F_j(x,y)}}{z(x,y)}$在这里加上 $z(x,y)$的目的是为了保证最后输出的结果是一个概率的形式，也就是做了一个 normilazition的操作，所以 $z(x,y)$在这里起到了一个全局作用，也正是因为如此， $z(x,y)$也是比较难计算的。接下来讲的CRF就是用到了这种思想。

CRF介绍

上面我们讲了log-linear model，所以我们的CRF也可以用这种模型来进行推导，所以CRF我们可以写成：

$p(y|x,w)=\dfrac{e^{\sum_jw_j\cdot F_j(x,y)}}{z(x,y)}$

这里的 $x$表示的是一个时序的序列，也就是随着时间变化而变化的一组数据，比如：文本，语音，天气，股票， $y$表示对应的状态或者叫标签。

因为 $x$和 $y$是一个时序的序列，在这里我们把公式修改一下：

$p(y|x,w)=\dfrac{e^{\sum_jw_j\cdot \sum_{i=2}f_j(y_{i-1},y_i,x,i)}}{z(x,y)}$

这里的 $i$表示时刻，这样修改表示我每一个时刻我只考虑当前状态 $y_i$和上一状态 $y_{i-1}$，最后再将所有的关系相加表示整个时序的信息，其实和上一个公式是一样的，只是我们把 $y$拆开来对待了。如下图

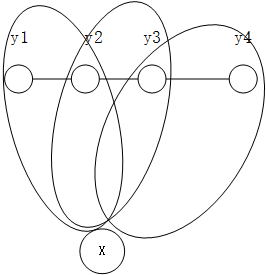
CRF的两个问题

与HMM算法一样，我们在这里也要解决同样的两个问题1、inference问题，也就是给定参数 $w$和数据 $x$求出对应状态 $y$ 。2、参数优化的问题，也就是给定数据和标签优化参数 $w$。下面我们来对这两个问题进行分别考虑 :

inference问题

给定 $w和x$求出对应标签 $y$对于这个问题其实和HMM的情况是类似的我们也是采用的动态规划也就是维特比算法来进行求解的，下面看一下公式的推导：

$\overline y=argmax\quad p(y|x,w)=argmax\quad \dfrac {1}{z(x,w)}\cdot e^{ \sum_j w_j\cdot F_j(x,y)}$

对于任何的 $\overline y$我们在计算时都是计算同样的 $z(w,x)$，因为 $z(w,x)$只依赖与 $w$和 $x$，毕竟我们求的是最大概率的那个 $y,$ 因此在公式中我们可以去掉 $z(w,x)$:和 $e$

$\overline y=argmax\quad \sum_jw_j\cdot F_j(x,y)=argmax \sum_jw_j\cdot \sum_{i=2}f_j(y_{i-1},y_i,x,i)$

令 $g(y_{i-1},y_i)=\sum_j w_j\cdot f_j(y_{i-1},y_i,x,i)$

$\overline y=argmax\quad \sum_{i=2}g_i(y_{i-1},y_i)$

就如同HMM的计算过程一样我们使用了维特比算法：

这里设置函数 $u(k,v)$，k表示的是当前时刻，v表示的是对应当前时刻选择的标签也就是 $y_v$,那么 $u(k,v)$表示k-1时刻到 $v$点最好的那个路径：

因此 $u(k,v)=max\sum_1^{k-1}g_i(y_{i-1},y_i)+g_k(y_{k-1},v)$

我们再将公式拆分一下：

$u(k,v)=max_{y_k-1}[max\sum_1^{k-2}g_i(y_{i-1},y_i)+g_{k-1}(y_{k-2},y_{k-1})]+g_k(y_{k-1},v)$

由上式我们可以知道 $[ \quad]$内部相当于求 $k-1$时刻所有点的最优路径，于是我们总结一下令 $y_{k-1}=c$这样公式就变成了：

$u(k,v)=max_{c}[u(k-1,c)+g_k(c,v)]$

典型的动态规划解决问题

优化参数问题

优化参数问题一般都是用梯度下降法，也就是对参数求导，找到收敛的方向，CRF也是这样做的：

对于 $p(y|x,w)=\dfrac{e^{\sum_jw_j\cdot F_j(x,y)}}{z(x,w)}$对 $w$进行求导在这里我们做了一点改变求 $\dfrac{\partial}{\partial w}\log p(y|x,w)$:

$\dfrac{\partial}{\partial w}\log p(y|x,w)=\dfrac{\partial}{\partial w}\cdot[{\sum_jw_j\cdot F_j(x,y)}-\log z(x,w)]=F_j(x,y)-\dfrac{1}{z(x,w)}\cdot\dfrac{\partial}{\partial w}z(x,w)$:

$z(x,w)$的目的是为了做normlazation。所以它是一个全局的变量，在crf中它就是考虑到的所有 $y$的集合：

$z(x,w)=\sum_{y`} e^{\sum_jw_j\cdot F_j(x,y`)}$

我们先来求： $\dfrac{\partial}{\partial w}z(x,w)$

$\dfrac{\partial}{\partial w}z(x,w)=\dfrac{\partial}{\partial w}\sum_{y`}{e^{\sum_jw_j\cdot F_j(x,y`)}}=\sum_{y`}\dfrac{\partial}{\partial w} e^{\sum_jw_j\cdot F_j(x,y`)}=\sum_{y`}{e^{\sum_jw_j\cdot F_j(x,y`)}}\cdot \dfrac{\partial}{\partial w}\sum_jw_j\cdot F_j(x,y`)$

$=\sum_{y`}{e^{\sum_jw_j\cdot F_j(x,y`)}}\cdot F_j(x,y`)$

将 $\dfrac{\partial}{\partial w}z(x,w)$代入公式中得：

$\dfrac{\partial}{\partial w}\log p(y|x,w)=F_j(x,y)-\dfrac{1}{z(x,w)}\cdot\sum_{y`}{e^{\sum_jw_j\cdot F_j(x,y`)}}\cdot F_j(x,y`)=F_j(x,y)- \sum_{y`}F_j(x,y`)\cdot\dfrac{{e^{\sum_jw_j\cdot F_j(x,y`)}}}{z(x,w)}$

$=F_j(x,y)- \sum_{y`}F_j(x,y`)\cdot p(y^`|x,w)=F_j(x,y)-E_{y^`\sim p(y^`|x,w)}\{F_j(x,y^`)\}$

最后一步是根据期望的定义计算出来的。

为了方便计算这里先来化简一下 $z(x,w)$

$z(x,w)=\sum_{y`} e^{\sum_jw_j\cdot F_j(x,y`)}=\sum_{y`} e^{\sum_jw_j\cdot \sum_{i=2}f_j(y^`_{i-1},y^`_i,x,i)}=\sum_{y`} e^{\sum_{i=2}g_i(y`_{i-1},y`_i)}$

$\sum_{y`} e^{\sum_{i=2}g_i(y`_{i-1},y`_i)}$的意思是考虑到了所有y的组合，假设 $y$有m种时长为 $n$，如果全部列出来，那么一共有 $m^n$种组合。显然这种做法时间复杂度太高，所以这里用到了动态规划的思想。

$\gamma(k+1,v)$表示 $k+1$时刻选择的标签是 $v$那么公式为：

$\gamma(k+1,v)=\sum_{y_1:y_k}e^{\sum_{i=2}^{k}g_i(y^`_{i-1},y^`_i)+g_{k+1}(y_k,v)}$

再将该式展开到 $k$层令 $y_k=u$表示 $y_k$时刻所可能的状态

$=\sum_u(\sum_{y_1:y_{k-1}}e^{\sum_{i=2}^{k}g_i(y^`_{i-1},y^`_i)}\cdot e^{g_{k}(y_{k-1},u)})\cdot e^{g_{k+1}(y_{k},v)}$

$()$里面的就是 $\gamma(k,u)$因此我们可以写成：

$\gamma(k+1,v)=\sum_u\gamma(k,u)\cdot e^{g_{k+1}(y_{k},v)}$

我们称这种算法为向前算法

同理我们也可以从后往前推导, $u$表示的是 $y_k$。

$\beta(u,k)=\sum_v[e^{g_{k+1}(u,v)}]\cdot\beta(u,k)$

这也表明通过向后算法我们可以计算出k时刻以后的所有组合 。

所以我们的
$z(x,w)=\sum_u\gamma(k,u)\cdot \beta(u,k)$

以上是针对离散型随机变量。

现在我们可以计算出 $p(y_k=u|x,w)=\dfrac{\gamma(k,u)\cdot \beta(u,k)}{z(x,w)}$

所以我们可以计算出(可以参考HMM)：

$p(y_k=u，y_{k+1}=v|x,w)=\dfrac{\gamma(k,u)\cdot e^{g_{k+1}(u,v)}\beta(v,k+1)}{z(x,w)}$

最后回到我们的公式：

$\dfrac{\partial}{\partial w}\log p(y|x,w)=F_j(x,y)-E_{y^`\sim p(y^`|x,w)}\{F_j(x,y^`)\}=F_j(x,y)-E_{y^`\sim p(y^`|x,w)}\{\sum_{i=2}f_j(y^`_{i-1},y^`_i,x,i)\}$

$=F_j(x,y)-\sum_{i=2}E_{y^`\sim p(y^`|x,w)}\{f_j(y^`_{i-1},y^`_i,x,i)\}=F_j(x,y)-\sum_{i=2}E_{y_i,y_{i-1}}\{f_j(y^`_{i-1},y^`_i,x,i)\}$

$=F_j(x,y)-\sum_{i=2}\sum_{y_i}\sum_{y_{i-1}}\{f_j(y^`_{i-1},y^`_i,x,i)\}\cdot p(y_i,y_{i-1}|x,w)$

$=F_j(x,y)-\sum_{i=2}\sum_{y_i}\sum_{y_{i-1}}\{f_j(y^`_{i-1},y^`_i,x,i)\}\cdot\dfrac{\gamma(i-1,y_{i-1})\cdot e^{g_{k+1}(y_{i-1},y_i)}\beta(y_i,i)}{z(x,w)}$

这些公式我们都可以进行更新参数：

$w^{t+1}=w^t-\eta\dfrac{\partial}{\partial w}\log p(y|x,w)$