本章笔记会有部分选取自《3D数学基础：图形与游戏开发》一书

仿射变换：包括平移和线性变换（旋转、切变等）
使用齐次坐标表示时，向量表示为(x, y, z, 0)，而点表示为(x, y, z, 1)。

4.1基本变换（Basic Transforms）

本章描述的大部分变换的摘要

4.1.1平移（Translation）

平移公式

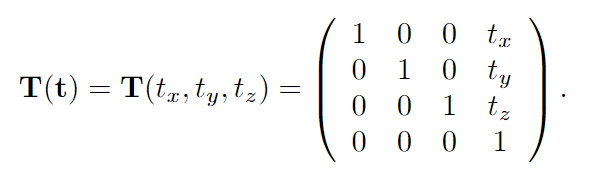
4.1.2旋转（Rotation）

与平移同样，是一种刚体变换（rigid-body transform），即，它保留了变换点之间的距离，并保留了手性（handedness）（即不会翻转左右）

绕原点逆时针旋转φ°的旋转矩阵R（2D）：

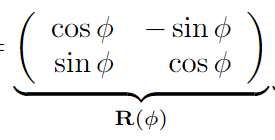
绕单个坐标轴逆时针旋转φ°的旋转矩阵R（3D）：

4.1.3缩放（Scaling）

沿坐标轴缩放
缩放矩阵

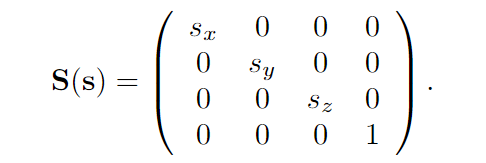
若缩放矩阵中含有一个或三个比例因子为负值，则其表示一种反射矩阵，也称为镜像矩阵。
如果只有两个比例因子为-1，那么将旋转弧度π。

反射矩阵被检测到时，通常会被“特殊对待”。
例如，当顶点由逆矩阵转换时，其顶点具有逆时针顺序的三角形将得到顺时针顺序。此顺序更改可能导致不正确的照明和背面剔除。

沿特定轴缩放：
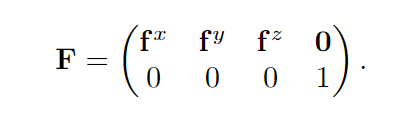
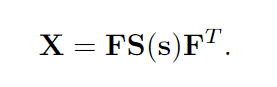
在这里插入图片描述

4.1.4切变（Shearing）

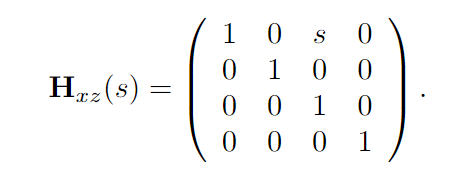
在这里插入图片描述

4.1.5变换的连接（Concatenation of Transform）

以上的基本仿射变换都可以通过左乘点的方式连接起来，如：
TRSp即为先缩放再旋转再平移，矩阵的位置不得交换（满足结合律但不满足交换律）
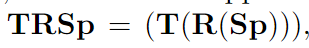
在这里插入图片描述

4.1.6刚体变换（The Rigid-Body Transform）

不涉及图像的形状变化的变换——刚体变换，其变换矩阵X写作以下形式：
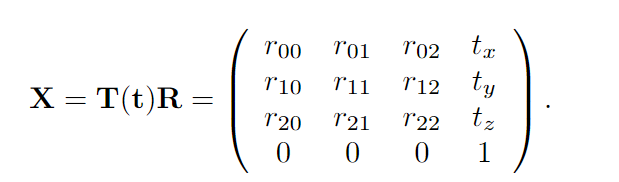
在这里插入图片描述

4.1.7法线变换（Normal Transform）

法线常常不能与物体做相同的变换，如图：
在这里插入图片描述
代替乘以矩阵本身，合适的方法是使用变换矩阵的伴随矩阵的转置矩阵。

4.1.8逆计算（Computation of Inverses）

在许多情况下，例如在坐标系之间来回切换时，需要逆矩阵。
根据有关转换的可用信息，可以使用以下三种计算矩阵逆的方法之一：

如果矩阵是单个变换或具有给定参数的简单变换序列，则可以通过“反转参数”矩阵阶数来轻松计算矩阵。如，M = T(t)R(φ),则M^(-1) = R(-φ)T(-t)。
如果已知矩阵正交，即转置为逆。
如果什么都不知道，则可以使用伴随方法，克莱默法则，LU分解或高斯消去法来计算逆。通常最好使用Cramer规则和伴随方法，因为它们的分支运算较少。

4.2特殊的矩阵运算和变换（Special Matrix Transform and Operation）

4.2.1 欧拉变换（The Euler Transform）

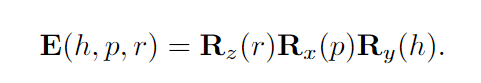
在这里插入图片描述
矩阵的顺序可以以24种（24种应该是以A⁴₄算得，但是明明只有3个矩阵，难道E矩阵也算在内？）不同的方式选择，这是最常用的一种。

优点：

使用直观、方便
任意数值都是合法的
最简洁的表达方式

缺点：

不方便差值（不同的值也可以表示同一个角）
存在万向锁问题

4.2.2 从欧拉变换中提取参数

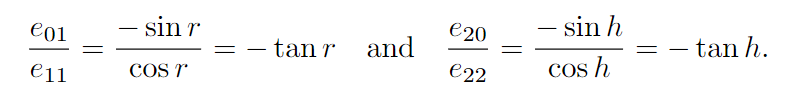
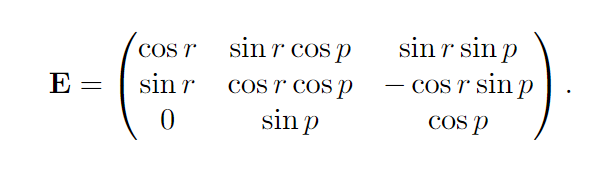
在这里插入图片描述

4.2.3 矩阵分解（Matrix Decomposition）

从级联矩阵中检索各种变换的任务称为矩阵分解
检索一组转换的原因很多，包括：

仅提取对象的比例因子
查找特定系统所需的变换。（例如，某些系统可能不允许使用任意4x4矩阵。）
确定模型是否仅经历了刚体变换。
在动画中的关键帧之间进行插值，其中只有对象的矩阵可用。
从旋转矩阵中剪切。

4.2.4 绕任意轴旋转（Rotation about an Arbitrary Axis）

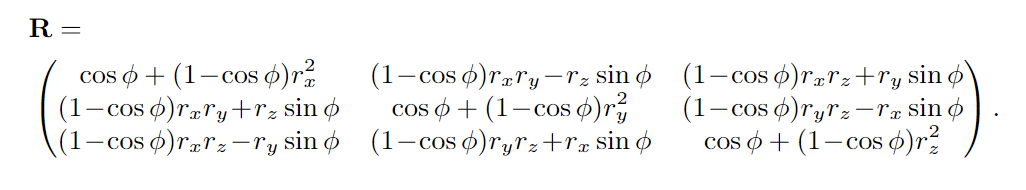
在这里插入图片描述

4.3 四元数（Quaternions）

优点：

平滑插值。slerp 和 squad 提供了方位间的平滑插值，没有其他方法能提供平滑插值。
快速连接和角位移求逆。四元数叉乘能将角位移序列转换为单个角位移，用矩阵作同样的操作明显会慢一些。四元数共提供了一种有效计算反角位移的方法，通过转置旋转矩阵也能达到同样的目的，但不如四元数来得容易。
能和矩阵形式快速转换。四元数和矩阵间的转换比欧拉角与矩阵之间的转换稍微快一点。
仅用四个数。四元数仅包含4个数，而矩阵用了9个数，它比矩阵“经济”得多(当然仍然比欧拉角多33%)。

缺点：

比欧拉角稍微大一些。这个额外的数似乎没有太大关系，但在需要保存大量角位移时，如存储动画数据，这额外的33%也是数量可观的。
四元数可能不合法。坏的输入数据或浮点数舍入误差积累都可能使四元数不合法(能通过四元数标准化解决这个问题，确保四元数为单位大小)。
难于使用。在所有三种形式中，四元数是最难于直接使用的。

四元数q可如下定义：
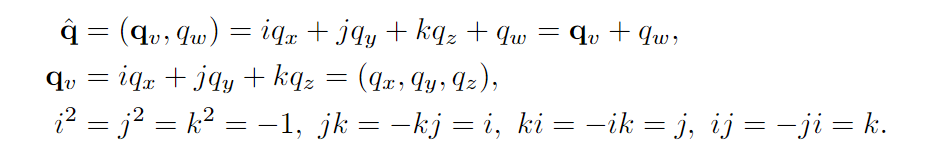
在这里插入图片描述
四元数相乘：

相加、共轭、规范化、四元数i

----以下省略许多四元数计算公式----

4.4 顶点混合（Vertex Blending）

在这里插入图片描述

缺点是可能会发生不必要的折叠，扭曲和自相交

4.5 变形（Morphing）

假设一个模型在时间t0显示，我们希望它在时间t1变为另一种模型。
对于t0和t1之间的所有时间，都使用某种插值获得了一个连续的混合”模型，此即为变形。
变形涉及解决两个主要问题，即顶点对应问题和插值问题。

通常用于一些运动或表情变化。

4.6 几何高速缓存回放（Geometry Cache Playback）

目的：减少高数量顶点动画的储存所占容量。
首先，使用量化。例如，位置和纹理坐标使用每个坐标的16位整数存储
进行空间和时间预测并编码差异。例如，如果某个顶点通过增量矢量从frame n - 1移动到frame n，则很可能以与frame n + 1相似的量移动。这些技术大大减少了存储量，因此该系统可以用于实时流数据。