《王道》树--PART2
4 树的应用
4.1 二叉排序树
二叉排序树,又叫二叉查找树,它或者是一棵空树;或者是具有以下性质的二叉树:
1. 若它的左子树不空,则左子树上所有节点的值均小于它的根节点的值;
2. 若它的右子树不空,则右子树上所有节点的值均大于它的根节点的值;
3. 它的左右子树也分别为二叉排序树。
如下图所示:
根据二叉排序树的定义,有左子树结点值<根结点值<右子树结点值,所以,对二叉排序树进行中序遍历,可以得到一个递增的有序序列。
例3 判断一棵二叉树是不是二叉排序树
//判断一棵二叉树是不是二叉排序树
//思路:二叉排序树的特点是,若左子树非空,则左子树上结点的值均小于根结点的值;
//若右子树非空,则右子树上结点的值均大于根结点的值。所以根据这一特点,可以看出
//二叉排序树的中序遍历是一个递增序列。
#include<iostream>
#include <limits.h>
using namespace std;
int prev1 = INT_MIN; //定义为最小的整数。宏定义INT_MIN在头文件limits.h中
typedef struct BiTreeNode
{
int data;
BiTreeNode* lchild;
BiTreeNode* rchild;
BiTreeNode(int x) : data(x), lchild(NULL), rchild(NULL) {}
};
int JudgeBST(BiTreeNode *root)
{
int b1, b2;
if (root == NULL)
return 1;
else
{
b1 = JudgeBST(root->lchild);
if (b1 == 0 || prev1 >= root->data)
return 0;
prev1 = root->data;
b2 = JudgeBST(root->rchild);
return b2;
}
}
//***********测试代码************
// 10
// /
// 7
// /\
// 4 8
// \
// 9
int main()
{
//生成一棵二叉树
BiTreeNode* Node1 = new BiTreeNode(10);//生成节点
BiTreeNode* Node2 = new BiTreeNode(7);
BiTreeNode* Node3 = new BiTreeNode(4);
BiTreeNode* Node4 = new BiTreeNode(8);
BiTreeNode* Node5 = new BiTreeNode(9);
Node1->lchild = Node2;//连接节点
Node2->lchild = Node3;
Node2->rchild = Node4;
Node5->rchild = Node5;
int p = JudgeBST(Node1);
cout << p << endl;
system("pause");
return 0;
}
4.2 平衡二叉树
为了避免树的高度增长过快,降低二叉排序树的性能,我们规定插入和删除二叉树结点时,要保证任意结点的左、右子树高度差的绝对值不超过1,并将这样的二叉树称为平衡二叉树(Balanced Binary Tree)又被称为AVL树。定义结点左子树与右子树的高度差为该结点的平衡因子,则平衡二叉树的平衡因子的值只可能是-1,0,1。
因此,平衡二叉树可定义为它或者是一棵空树,或者是具有下列性质的二叉树:它的左子树和右子树都是平衡二叉树,且左子树和右子树的高度差的绝对值不超过1。例如,下图中的二叉树就是一棵平衡二叉树。
例4 判断一棵二叉树是不是平衡二叉树
有了求二叉树的深度的经验之后再解决这个问题,我们很容易就能想到一个思路:在遍历树的每个结点的时候,调用函数TreeDepth得到它的左右子树的深度。如果每个结点的左右子树的深度相差都不超过1,按照定义它就是一棵平衡的二叉树。
//=============方法1==============
/*求二叉树的深度*/
int TreeDepth(BinaryTreeNode *pRoot){
if (pRoot == NULL){
return 0;
}
int nLeft = TreeDepth(pRoot->m_pLeft);
int rRight = TreeDepth(pRoot->m_pRight);
return (nLeft > nRight) ? (nLeft + 1) : (nRight + 1);
}
//需要重复遍历结点的算法,不够好
bool IsBalanced_Solution1(BinaryTreeNode *pRoot){
if (pRoot == NULL)
return true;
int left = TreeeDepth(pRoot->m_pLeft);
int right = TreeDepth(pRoot->m_pRight);
int diff = left - right;
if (diff > 1 || diff < -1)
return false;
return IsBalanced_Solution1(pRoot->m_pLeft) && IsBalanced_Solution1(pRoot->m_pRight)
}
上面的代码固然简洁,但我们也要注意到由于一个结点会被重复遍历多次,这种思路的时间效率不高。例如在IsBalancedBinaryTree方法中输入上图中的二叉树,我们将首先判断根结点(结点1)是不是平衡的。此时我们往函数TreeDepth输入左子树的根结点(结点2)时,需要遍历结点4、5、7。接下来判断以结点2为根结点的子树是不是平衡树的时候,仍然会遍历结点4、5、7。毫无疑问,重复遍历同一个结点会影响性能。
在上面的代码中,我们用后序遍历的方式遍历整棵二叉树。在遍历某结点的左右子结点之后,我们可以根据它的左右子结点的深度判断它是不是平衡的,并得到当前结点的深度。当最后遍历到树的根结点的时候,也就判断了整棵二叉树是不是平衡二叉树。
//=========方法2==============
//后序每个结点只遍历一次,一边遍历一边记录它的深度
bool IsBalanced(BinaryTreeNode *pRoot, int *pDepth){
if (pRoot == NULL){
*pDepth = 0;
return true;
}
int left, right;
if (IsBanlanced(pRoot->m_pLeft,&left) && IsBanlanced(pRoot->m_pRight, &right)){
int diff = left - right;
if (diff <= 1 && diff >= -1){
*pDepth = 1 + (left > right ? left : right);
return true;
}
}
return false;
}
bool IsBanlanced_Solution2(BinaryTreeNode* pRoot)
{
int depth = 0;
return IsBalanced(pRoot, &depth);
}
//=========方法3==============
//下面方法也是可行的,且形式更加简洁。求出根结点的最大深度与最小深度,则最大深度与最小深度之差dis就是树中任一子树深度差最大值,所以只要dis小于等于1,此树就是平衡二叉树。
int maxDepth(TreeNode *root){
if (root == NULL)
return 0;
return 1 + max(maxDepth(root->left), maxDepth(root->right));
}
int minDepth(TreeNode *root){
if (root == NULL)
return 0;
return 1 + min(minDepth(root->left), minDepth(root->right));
}
bool isBanlanced(TreeNode *root){
return (maxDepth(root) - minDepth(root) <= 1);
}
*平衡二叉树的插入问题
*红黑树
4.3 哈夫曼树及哈夫曼编码
1.哈夫曼树的构造
对于最优二叉树,权值越大的结点越接近树的根结点,权值越小的结点越远离树的根结点。
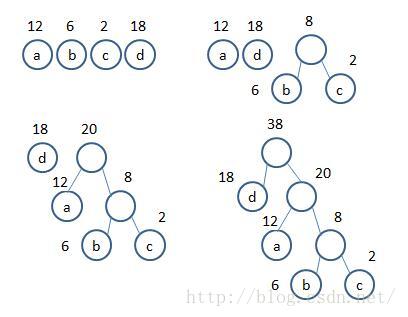
最优二叉树的构造算法步骤:
(1)根据给定的n个权值w1,w2,...,wn构成n棵二叉树森林F={T1,T2,...,Tn},其中每一棵二叉树Ti中都只有一个权为wi的根结点,其左、右子树为空。
(2)在森林F中选出两棵根结点权值最小的树作为一棵新二叉树的左、右子树,新二叉树的根结点的权值为其左、右子树根结点的权值之和。
(3)从F中删除这两棵二叉树,同时把新二叉树加入到F中。
(4)重复步骤(2)、(3),直到F中只含有一棵树为止,此树便为最优二叉树。
哈夫曼树的构造过程示意图如下:
2.哈夫曼树的编码
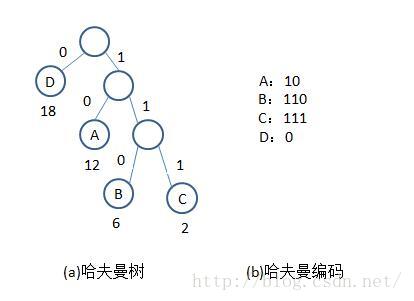
哈夫曼编码是一种变长编码。其定义如下:
对于给定的字符集D={d1,d2,...,dn}及其频率分布F={w1,w2,...,wn},用d1,d2,...,dn作为叶结点,w1,w2,...,wn作为结点的权,利用哈夫曼算法构造一棵最优二叉树,将树中每个分支结点的左分支标上"0";右分支标上"1",把从根到每个叶子的路径符号("0"或"1")连接起来,作为该叶子的编码。
哈夫曼编码是在哈夫曼树的基础上求出来的,其基本思想是:从叶子结点di(0<=i<n)出发,向上回溯至根结点,依次求出每个字符的编码。
示例:对于字符集D={A,B,C,D},其频率(单位:千次)分布为F={12,6,2,18},下图给出D的哈夫曼编码图。