《王道》树--PART1
1 树的基本概念和性质
树(Tree)是n(n>=0)个结点的有限集。
在任意一棵非空树中:
1)有且仅有一个特定的称为根(Root)的结点;
2)当n>1时,其余结点可分为m(m>0)个互不相交的有限集T1,T2,...,Tn,其中每个集合本身又是一棵树,并称为根的子树(SubTree)
1.1 度
结点拥有的子树树称为结点的度(Degree)如:上图A的度为3,C的度为1,F的度为0。
度为0的结点称为叶子(Leaf)或终端结点,如:上图K,L,F,G,M,I,J都是树的叶子
度不为0的结点称为非终端结点或分支结点,如:上图A,B,C,D,E,H
树的度是树内各节点的度的最大值,如:上图的树的度为 3 。
1.2 结点(家谱图)
结点的子树的根称为该结点的孩子(Child),相应地,该结点称为孩子的双亲(Parent)如:上图D是A的孩子,A是D的双亲。
同一个双亲的孩子叫兄弟(Sibling)如:上图H,I,J为互为兄弟
其双亲在同一层的结点互为堂兄弟。如上图G与E、F、H、I、J互为堂兄弟
结点的祖先是从根到该结点所经分支上的所有结点。如:上图M的祖先为A、D、H
1.3 层次,深度(你家几代同堂啊?)
结点的层次(Level)从根开始定义起,根为第一层,根的孩子为第二层
树中结点的最大层次成为树的深度(Depth)或高度。如:上图树的深度为4
1.4 有序树与无序树(长子,次子。。。)
树中结点的各子树看成从左至右是有次序的(即不能互换),则称该树为有序树,否则成为无序树。
有序树中最左的子树的根称为第一个孩子,最右边的称为最后一个孩子。(毕竟有序,排好了谁是老大,谁是老二,长兄有序嘛)
森林(Forest)是m(m>=0)棵互不相交的树的集合。对树中每个结点而言,其子树的集合即为森林。
由此也可以森林和树相互递归的定义来描述树。
1.5 树的基本性质
2 二叉树
2.1 二叉树概念
二叉树是另一种树形结构(是n(n>=0)个结点的有限集合),其特点是每个结点至多只有两棵子树(即二叉树中不存在度大于2的结点),并且,二叉树的子树有左右之分,其次序不能颠倒。
二叉树是有序树,若将其左、右子树颠倒,就成为另一棵不同的二叉树。即使树中只有一棵子树,也要区分它是左子树还是右子树。
注意:
二叉树与度为2的有序树的区别:度为2的树至少有3个结点。而二叉树可为空;度为2的有序树的孩子结点的左右次序是相对于另一孩子结点而言的,如果某个结点只有一个孩子结点,这个孩子结点就无须区分其左右次序,而二叉树无论其孩子数是否为,均需确定其左右次序,也就是说二叉树的结点次序不是相对于另一结点而言的,而是确定的。
2.2 二叉树性质
接下来的描述中有必要用到一些数学符号,在博客中不好画出,因此我们规定一些符号——
- a^b—— a的b的次方 (计算机常用,无需多言)
- int_UP()—— 向上取整(即去掉浮点数的小数部分,然后将整数部分加1)
- int_DOWN()—— 向下取整(即去掉浮点数的小数部分,只留整数部分)
- log(a,b) —— 表示以a为底取b的对数
1.非空二叉树上叶子结点数等于度为2的结点数加1,即N0=N2+1。
2.非空二叉树上第K层上至多有2^(K-1)个结点(K>=1)。
3.高度为H的二叉树上至多有2^(H-1)个结点(H>=1)。
4.对完全二叉树按从上到下、从左到右的顺序依次编号1,2,……,N,则有以下关系:
1)当i>1时,结点i的双亲结点编号为int_DOWN(i/2),即当i为偶数时,其双亲结点的编号为i/2,它是双亲结点的左孩子;当i为奇数时,其双亲结点的编号为(i-1)/2,它是双亲结点的右孩子;
2)当2i<=N时,结点i的左孩子编号为2i,否则无左孩子;
3)当2i+1<=N时,结点i的右孩子编号为2i+1,否则无右孩子;
4)结点i所在层次(深度)为int_DOWN(log(2,i))+1;
5.具有N个(N>0)结点的完全二叉树的高度为int_UP(log(2,N+1))或int_DOWN(log(2,N))+1。
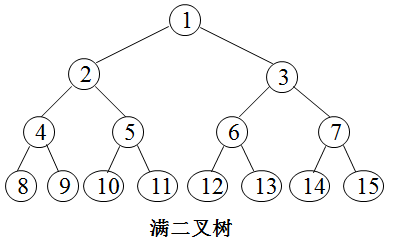
2.3 满二叉树
一棵高度为h,并且含有2^h-1个结点的二叉树称为满二叉树,即树中的每一层都含有最多的结点。满二叉树的叶子结点都集中在二叉树的最下一层,并且除叶子结点之外的每个结点度数均为2。
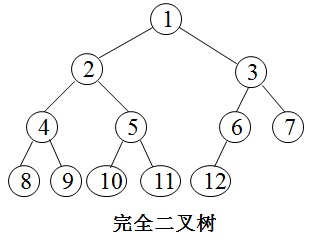
2.4 完全二叉树
设一个高度为h,有n个结点的二叉树,当且仅当其每一个结点都与高度为h的满二叉树中编号为1~n的结点一一对应时,称为完全二叉树。这种树的特点如下:
1)若i<=int_DOWN(n/2),则结点i为分支结点,否则为叶子结点;
2)叶子结点只可能在层次最大的两层上出现。对于最大层次中的叶子结点,都依次排列在该层最左边的位置上;
3)如果有度为1的结点,只可能有一个,且该结点只有左孩子而无右孩子;
4)按层序编号后,一旦出现某结点(其编号为i)为叶子结点或只有左孩子,则编号大于i的结点均为叶子结点;
5)若n为奇数,则每个分支结点都有左子女和右子女;若n为偶数,则编号最大的分支结点(编号为n/2)只有左子女,没有右子女,其余分支结点左、右子女都有。
2.5 二叉树的存储结构
1.顺序存储结构
顺序存储就是用一组地址连续的存储单元依次自上而下、自左向右存储完全二叉树的结点元素,即将完全二叉树编号为i的结点元素存储在某个数组下标为i-1的分量中。对于一般二叉树,则应将其每个结点与完全二叉树上的结点对照,存储在一位数组的相应分量中。
然而,在最坏的情况下,一个高度为H且只有H个结点的单支数却需要占据接近2^H-1个存储单元。因此,顺序存储结构一般仅适用于完全二叉树中。
2.链式存储结构
用链表来表示一棵二叉树,链表中每个结点由三个域组成,除了数据域外,还有两个指针域,分别用来给该结点左孩子和右孩子所在的链结点的存储地址。
2.6 二叉树的遍历
1. 遍历方法介绍
2. 先序、中序和后序遍历代码实现(递归和非递归)
构造方式:
#include <iostream>
#include <stack>
using namespace std;
typedef struct BiTNode{
char data;
int lvisited, rvisited; //左、右孩子是否访问过,1表示已访问(此项)
struct BiTNode *lchild, *rchild;
}BiTNode,*BiTree;
void InitBiTree(BiTree &T) //构造空二叉树
{
T = NULL;
}
void CreateBiTree(BiTree &T) //生成二叉树
{
char ch;
cin >> ch;
if (ch == '0') //0代表空
T = NULL;
else{
T = (BiTree)malloc(sizeof(BiTNode)); //生成根结点
if (!T){
cout << "生成结点错误!" << endl;
return;
}
T->data = ch;
T->lvisited = 0;
T->rvisited = 0;
CreateBiTree(T->lchild);
CreateBiTree(T->rchild);
}
}
三种遍历方式代码:
void PreOrder(BiTree T) //先序递归遍历(中左右)
{
if (T != NULL)
{
cout << T->data << " ";
PreOrder(T->lchild);
PreOrder(T->rchild);
}
}
void SqlPreOrder(BiTree T) //先序非递归遍历
{
stack<BiTree> s; //创建一个栈
BiTree p = T; //定义用来指向当前访问的结点的指针
while (p || !s.empty()) //直到当前结点p为NULL且栈空时,循环结束
{
if (p) //p不为空,栈空或不空
{
//从根结点开始,输出当前结点,并将其入栈,
//同时置其左孩子为当前结点,直至其没有左孩子,即当前结点为NULL
cout << p->data << " ";
s.push(p);
p = p->lchild;
}
else //p为空,栈空或不空
{
//如果当前节点p为NULL且栈不空,则将栈顶节点出栈,
//同时置其右孩子为当前节点,循环判断,直至p不为空
p = s.top();
p = p->rchild;
s.pop();
}
}
}
void InOrder(BiTree T) //中序递归遍历(左中右)
{
if (T != NULL)
{
InOrder(T->lchild);
cout << T->data << " ";
InOrder(T->rchild);
}
}
void SqInOrder(BiTree T) //中序非递归遍历
{
stack<BiTree> s;
BiTree p = T;
while (p || !s.empty())
if (p)
{
s.push(p);
p = p->lchild;
}
else
{
p = s.top();
cout << p->data << " ";
s.pop();
p = p->rchild;
}
}
void PostOrder(BiTree T) //后序递归遍历
{
if (T != NULL)
{
PostOrder(T->lchild);
PostOrder(T->rchild);
cout << T->data << " ";
}
}
//后序非递归遍历1思路:因为后序非递归遍历二叉树的顺序是先访问左子树,再访问右子树,最后
//访问根结点。当用堆栈来存储结点,必须分清返回根结点时,是从左子树返回的,还是从右子树
//返回的。所以,使用辅助指针r,其指向最近访问过的结点。
void SqlPostOrder1(BiTree T) //后序非递归遍历1
{
stack<BiTree> s;
BiTree p = T, r;
while (p || !s.empty())
{
if (p) //走到最左边
{
s.push(p);
p = p->lchild;
}
else //向右
{
p = s.top(); //取栈顶结点
if (p->rchild && p->rchild != r) //如果右子树存在,且未被访问过
{
p = p->rchild;
s.push(p);
p = p->lchild; //再走到最左
}
else //否则,访问栈顶结点并弹出
{
cout << p->data << " ";
r = p; //记录该结点
s.pop();
p = NULL; //结点访问完后,重置p指针
}
}
}
}
//思路2:在结点中增加标志域,记录是否已被访问。
void SqlPostOrder2(BiTree T) //后序非递归遍历2
{
stack<BiTree> s;
BiTree p = T;
while (p || !s.empty())
{
if (p && p->lvisited == 0) //左走,且左子树未被访问
{
p->lvisited = 1;
s.push(p);
p = p->lchild;
}
else
{
p = s.top();
if (p->rchild != NULL && p->rvisited == 0)//右子树未被访问,右走一步
{
p->rvisited = 1;
p = p->rchild;
}
else //访问栈顶元素并弹栈
{
cout << p->data << " ";
s.pop();
if (!s.empty())
p = s.top();
else //当最后一个元素弹栈出去后,结束
return;
}
}
}
}
3. 在按层次遍历二叉树的算法中,需要借助的辅助数据结构是队列。
3 二叉树的应用
3.1 判断两棵二叉树是否相同
不考虑左右结点可以旋转的情况下,如何判别两棵二叉树是否相等。此要求较为简单,通常大家都可以很快地写出递归代码:
//二叉树结点结构体
struct BinaryNode
{
int data;
BinaryNode * lc;
BinaryNode * rc;
}*BTree;
//判断二叉树是否相等的函数
bool isEqual(BTree T1, BTree T2)
{
if (T1 == NULL && T2 == NULL)
return true; //都为空,相等。
if (!T1 || !T2) //由于上面的判断不成立,则T1,T2至少有一个不为空
return false; //一个空,一个不空,不相等
if (T1->data == T2->data) //如果根节点相等
return isEqual(T1->lc, T2->lc) && isEqual(T1->rc, T2->rc); //判断左右子树是否都相等
else
return false;
}
由于是先比较根结点的值是否相等,然后再判断左右子树,显然上述代码是先序遍历。
比较两棵可以旋转的二叉树是否相等。二叉树的左右子结点可以旋转是指可以把二叉树的左结点旋转成为右结点,右结点旋转成为左结点。
只需将上述代码红色部分改为:
return (isEqual(T1->lc, T2->lc) && isEqual(T1->rc, T2->rc)) || (isEqual(T1->lc, T2->rc) && isEqual(T1->rc, T2->lc))
3.2 求二叉树的深度
思路:
我们可以从根节点即左右子树来理解二叉树的深度。对于任意一棵非空二叉树,有如下四种情况:
(1)如果二叉树为空,则深度为0
(2)如果一颗树只有一个节点,它的深度是1;
(3)如果根节点只有左子树而没有右子树,那么二叉树的深度应该是其左子树的深度加1;
(4)如果根节点只有右子树而没有左子树,那么二叉树的深度应该是其右树的深度加1;
(5)如果根节点既有左子树又有右子树,那么二叉树的深度应该是其左右子树的深度较大值加1;
//二叉树的结点定义
struct BinaryTreeNode{
int m_value;
BinaryTreeNode* m_pLeft;
BinaryTreeNode* m_pRight;
};
//求二叉树的深度
int treeDepth(BinaryTreeNode* root){
if (root == NULL){ //如果二叉树为空,则深度为0
return 0;
}
//分别计算左子树和右子树的深度
int nLeft = treeDepth(root->m_pLeft);
int nRight = treeDepth(root->m_pRight);
return nLeft>nRight ? nLeft + 1 : nRight + 1;
}
3.3 求二叉树中结点的最大距离
如果我们把二叉树看做图,父子节点之间的连线看成是双向的,我们姑且定义“距离”为两个节点之间边的个数。写一个程序求一棵二叉树中相距最远的两个节点之间的距离。
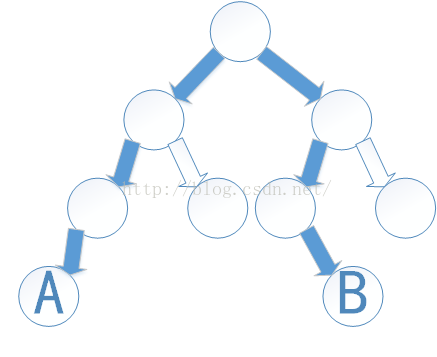
如下图所示,树中相距最远的两个节点为A,B,最大距离为6。
计算一个二叉树的最大距离有两个情况:
情况A: 路径经过左子树的最深节点,通过根节点,再到右子树的最深节点。
情况B: 路径不穿过根节点,而是左子树或右子树的最大距离路径,取其大者。
对于情况A来说,只需要知道左右子树的深度,然后加起来即可。
对于情况B来说,需要知道左子树的最远距离,右子树的最远距离。
只需要计算这两种情况的路径距离,并取其最大值,就是该二叉树的最大距离
struct NODE
{
int value; // 该结点的值
NODE *pLeft; // 左子树
NODE *pRight; // 右子树
};
//递归获取两个值:一个是子树的最大深度,一个是子树的结点间最大距离。
struct RESULT { //定义返回结果
int nMaxDistance; //最大距离
int nMaxDepth; //最大深度
};
RESULT GetMaxinumDistance(NODE *root) { //结点为空,则高度为0,结点最大距离为0
if (!root) {
RESULT empty = { 0,-1 }; //最大深度初始化为-1,是因为调用者要对其加1,然后变成0
return empty;
}
//分别递归左子树和右子树获取最大结点距离
RESULT lhs = GetMaxinumDistance(root->pLeft);
RESULT rhs = GetMaxinumDistance(root->pRight);
RESULT result;
result.nMaxDepth = max(lhs.nMaxDepth + 1, rhs.nMaxDepth + 1);
result.nMaxDistance = max(max(lhs.nMaxDistance, rhs.nMaxDistance), lhs.nMaxDepth + rhs.nMaxDepth + 2);
return result;
}
例1 一棵二叉树每个结点包含一个整数,请设计一个算法输出所有满足条件的路径,此路径上的所有结点之和等于给定值,注意此类路径不要求必须从必须从根结点开始。解题思路:利用先序遍历的递归算法遍历二叉树,采用数组记录遍历的路径,计算从根结点或者是之后的某一个结点开始至当前结点是否能满足条件,若可以则输出,否则返回上一层改变遍历方向重新计算。代码如下:
//一棵二叉树每个结点包含一个整数,设计一个算法输出所有满足条件的路径,
//此路径上的所有结点之和等于给定值,此类路径不要求必须从根结点开始
#include<iostream>
#include<vector>
using namespace std;
typedef struct BiTreeNode {
int data;
BiTreeNode *lchild;
BiTreeNode *rchild;
}*BiTree;
//从root结点开始向上遍历查找满足条件的路径
//sum结点之和的给定值,buffer记录从当前结点开始向上遍历的路径(此参数为引用),level记录当前结点root所在层次
void findSum(BiTree root, int sum, vector<int> &buffer, int level)
{
if (root == NULL) //递归出口
return;
int tmp = sum;
buffer.push_back(root->data); //记录下当前结点
//从当前结点开始,然后不断遍历与当前结点相连的上一层结点,直到能找到满足条件的路径再输出.
for (int i = level; i >= 0; i--)
{
tmp -= buffer[i];
if (tmp == 0) //当前路径满足,输出路径
{
for (int j = i; j <= level; j++)
cout << buffer[j] << " ";
cout << endl;
}
}
//从左孩子结点开始向上遍历
findSum(root->lchild, sum, buffer, level + 1);
//删除左孩子结点,从右孩子结点开始向上遍历
buffer.pop_back();
level -= 1;
findSum(root->rchild, sum, buffer, level + 1);
}
void CreateBiTree(BiTree &root)
{
int data;
while (cin >> data) {
if (data == 0)//输入为0时表示空结点
root = NULL;
else
{
root = new BiTreeNode();
root->data = data;
CreateBiTree(root->lchild);
CreateBiTree(root->rchild);
}
}
}
int main()
{
BiTree root = NULL;
CreateBiTree(root);
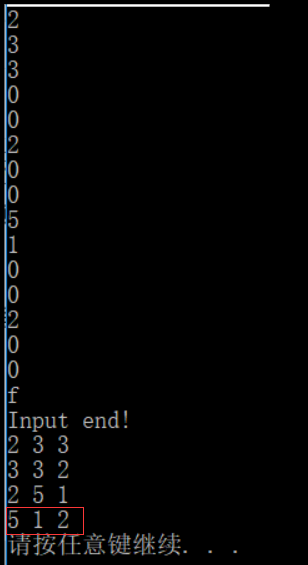
cout << "Input end!" << endl;
int sum = 8;//给定值
vector<int> buffer;
findSum(root, sum, buffer, 0);//从根结点即第0层开始
system("pause");
return 0;
}
3.4 由遍历序列构造二叉树
当给出一棵二叉树,我们可以知道它的先序、中序和后序遍历。那么我们是否能够根据先序、中序或者后序的遍历序列来还原出这棵二叉树呢?
首先通过二叉树的一种遍历序列是无法还原二叉树的。如果在二叉树的三种遍历序列中给出其中的两种,是否可以唯一确定一棵二叉树呢?
由二叉树的先序和中序遍历序列可以唯一确定一棵二叉树。因为,二叉树的先序遍历必先访问根结点D,其次遍历左子树L,然后遍历右子树R。即在先序遍历序列中,第一个结点必为根结点;而在中序遍历中,先遍历左子树L,然后访问根结点D,最后遍历右子树R,因此中序遍历序列被根分为两部分:根结点之前的部分为左子树结点中序序列,根结点之后的为右子树结点中序序列。通过这两部分再到先序序列中找到左右子树的根结点,以此类推,便可唯一得到一颗二叉树。
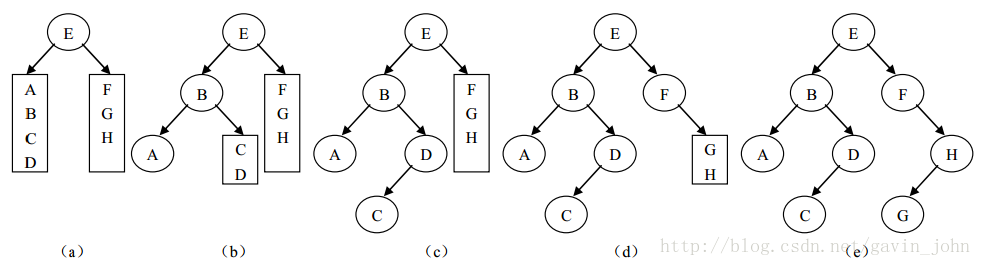
例如:已知一颗二叉树的先序序列为EBADCFHG,其中序序列为ABCDEFGH。下图说明了还原二叉树的过程:
同样的,由二叉树的后序和中序遍历序列也可以唯一确定一棵二叉树。还原的方法与上述类似,只不过此时根结点是出现在后序序列的最后面。
由先序和后序序列不能唯一确定一棵二叉树。例如,先序序列为AB,后序序列为BA,此时就无法确定二叉树的结构,因为B既可以是A的左子树,也可以是根A的右子树。
例2 输入某二叉树的前序遍历和中序遍历的结果,请重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6},则重建二叉树并返回。
参考博客
//二叉树的结点定义
struct BinaryTreeNode{
int m_nValue;
BinaryTreeNode* m_pLeft;
BinaryTreeNode* m_pRight;
};
//preorder 前序遍历
//inorder 中序遍历
BinaryTreeNode* Construct(int *preorder, int *inorder, int length){ //输入前序序列,中序序列和序列长度
if (preorder == NULL || inorder == NULL || length <= 0)
return NULL;
return ConstructCore(preorder, preorder + length - 1, inorder, inorder + length - 1);
}
BinaryTreeNode* ConstructCore(int *startPreorder, int *endPreorder, int *startInorder, int *endInorder){
//前序遍历序列的第一个数字是根结点的值
int rootValue = startPreorder[0];
BinaryTreeNode *root = new BinaryTreeNode(); //建立结点
root->m_nValue = rootValue;
root->m_pLeft = root->m_pRight = NULL;
if (startPreorder == endPreorder){
if (startInorder == endInorder && *startPreorder == *startInorder)
return root;
else
throw std::exception("Invalid input."); //非法输入
}
//在中序遍历中找到根结点的值
int *rootInorder = startInorder;
while (rootInorder <= endInorder && *rootInorder != rootValue)
++rootInorder;
if (rootInorder == endInorder && *rootInorder != rootValue)
throw std:exception("Invalid input");
int leftLength = rootInorder - startInorder;
int *leftPreorderEnd = startPreorder + leftLength;
if (leftLength > 0)
{
// 构建左子树
root->m_pLeft = ConstructCore(startPreorder + 1, leftPreorderEnd, startInorder, rootInorder - 1);
}
if (leftLength < endPreorder - startPreorder) //(中序序列)若还有左子树,则左子树序列长度应等于当前前序序列的长度
//若小于,说明已无左子树,此时建立右子树
{
// 构建右子树
root->m_pRight = ConstructCore(leftPreorderEnd + 1, endPreorder, rootInorder + 1, endInorder);
}
return root;
}