后缀树的实现（时间复杂度O(m^3)）

构建的基本思路：首先往树中插入最长的后缀即字符串本身，然后依次插入次长的后缀，重复此步骤直到插入最后一个空串；

1）插入串本身；//初始化操作

2）若上一个后缀为S，令S=aW（W为下一个后缀）。往树中插入后缀W，重复本操作直到S=$；

按照定义取做的话，算法的时间复杂度为O（m^3）

在这里我们只需要记录边集合即可，对于每条边保存该边的起始和结束位置，以及此边保存的字符串信息（起始&结束）

首先找出待插入串S=beta，存在两种情况。①在树中已经存在此字段不需要进行任何处理；②树中存在与之部分匹配的部分

或者不匹配，对于第二种情况的不存在匹配只需要创建一个叶子结点于根结点相连接即可、当对于存在部分匹配的情况时

只需要增加一个内部结点和一个叶结点即可（修改原边以及增加两条新边）。

#include<iostream>
#include<algorithm>
using namespace std;
#define N 10005
typedef struct E{
	int pre;
	int child;
	int start;
	int end;
}E;//边结构体 
E e[N];
int k=0;//边的数目 
int find(string s1,string s2){
	int l1=s1.length();
	int l2=s2.length();
	int m = l1>l2?l2:l1;//取最短边 
	int flag=0;
	for(int i=0;i<m;i++){
		if(s1[i]==s2[i]){
			flag++;
		}
		else{
			break;
		}
	}
	return flag;//匹配长度 
	//时间复杂度O(n) 
}
bool cmp(E a,E b){
	return a.pre<b.pre;//升序 
}
int count=0;
int main(){
	string str;
	cin>>str;//读取字符串 
	e[0].pre=-1;
	e[0].child=0;
	e[0].start=0;
	e[0].end=str.length(); //初始化结点 
	for(int i=1;i<str.length();i++){
		string beta=str.substr(i);//获取当前的串
		int root=-1;//从根结点开始遍历 
		sort(e,e+k,cmp);//类似于快速排序 O（nlogn） 
		for(int j=0;j<=k;j++){ 
			if(e[j].pre==root&&beta[0]==str[e[j].start]){//找到根结点 
				int length=find(str.substr(e[j].start,e[j].end),beta);//匹配成功长度 
				//cout<<"截取字符"<< str.substr(e[j].start,e[j].end)<<endl;
				if(length==beta.length()){
					root=0; 
					break; 
					//不做任何处理 ，如果此串已经匹配成功 
				}
				else if(length<beta.length()){
					//此串要么在中间匹配中断，要么沿着某一路径继续匹配； 
					int lt=e[j].end-e[j].start;//当前串的长度 
					root=e[j].child;
					//插入一个内结点和一个叶子结点 
					if(lt>length){
							k++;
							e[j].child=k;
							e[j].end=e[j].start+length;
							e[k].pre=k;
							e[k].child=root;
				    		e[k].start=e[j].end;
							e[k].end=e[k].start+lt-length;
							k++;
							e[k].pre=k-1;
							e[k].child=k;
							e[k].start=i+length;
							e[k].end=i+beta.length();//线性时间复杂度 
							break;
					}
				}
			}
		}
		if(root==-1){
			k++;//创建叶子结点 
			e[k].pre=root;
			e[k].child=k;
			e[k].start=i;
			e[k].end=i+beta.length();
			//未找到匹配字符串 
		}
	}
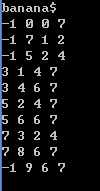
	//打印输出后缀树 
	for(int l=0;l<=k;l++){
		cout<<e[l].pre<<" "<<e[l].child<<" "<<e[l].start<<" "<<e[l].end<<endl;
	}
	cout<<endl;
	return 0;
}

运行结果：