一、后缀树的定义:通过一个树可以表示所有可能的后缀子串;
例子:S=acacag;
1)每一条边用一个字符串标记;2)所有的后缀可以从根结点到所有叶结点的路径读出;
3)结束标记符“$”(避免某些后缀是其他后缀的前驱);
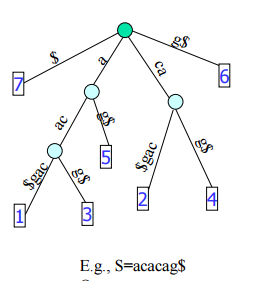
后缀树的特点:1)长度为n的字符串,其后缀树恰好有n个叶子结点(因为有n个后缀);
2)每一条边可以用个数据表示(在原来字符串的起始位置和结束位置);
3)在一个后缀树中至多有2n-1个结点;
证明:首先已知有n个叶子结点其度数为0,除了根结点和叶子结点每一个内部结点
的度数为2,根结点度数不定设为x,x的取值范围为【2,n0】
在这里设叶子结点为n0,度数为2的结点为n2,总结点个数为n
易得:n=n0+n2+1;//这里的1为根结点
由度数的关系可得出:2*n2+x+1=n;//叶结点不提供分支,根结点提供x个分支,其余结点提供2个分支
联立上述两式子可得出:n=2n0+1-x;即可得出节点总数n的取值范围为【n0+1,2n0-1】
4)一个后缀树可以用O(nlogn)位表示;
二、后缀树的简单应用
1)在S中找出所有的出现Q的子串个数:从根结点出发,沿着唯一的路径Q到达点x,所有x以下的叶子结点均为出现过Q的子串
时间复杂度为O(|Q|+出现次数)总体上呈现线性级;
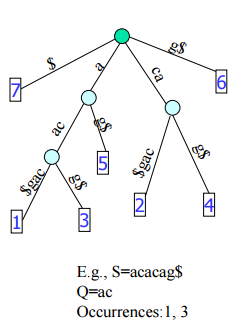
2)找出S中的最长重复子串:找出具有最大深度的内结点,其所对应的路径即为最长重复子串
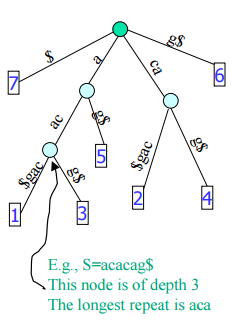
时间复杂度为O(n)
3)求解不同序列的最长公共子序列:将不同序列S全部构建在一个后缀树中,每个叶子结点用不同的结点加以标记,找出
具有最大深度的内部结点且此结点同时包含不同串的后缀;
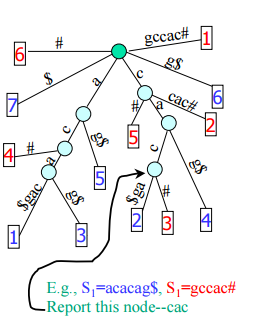
除此之外还有其他应用:如最长匹配 、最大回文、最长公共前驱等等;(算法的时间复杂度为O(n))
三、后缀树构造算法(复杂度O(n^2)):

1)首先初始化一个树只有一个根结点;O(1)
2)之后循环遍历n次,将各个后缀子串加入到这棵树中;O(n^2)
四、隐含后缀树(方法):1)将所有的边中的$全部删除;2)去除所有没有标记的边;3)删除只有一个孩子的结点;
(如图所示:隐含后缀树中没有结束标记符,且每个内部结点的孩子个数大于等于2,边值用于保存路径信息)
隐含后缀树

Rule1:如果在树中发现与当前匹配S【j,i】的路径且终止于一个叶子结点,即将S【i+1】加入这条边的末尾即可;
Rule2:如果在树中发现与当前匹配S【j,i】的路径但其后面的元素不是S【i+1】建立一个新的叶子结点,以及一个
新的内部结点,新旧结点的边标记为S【i+1】,这个新的叶结点标记为i;
Rule3:如果从根节点开始的标记为S【j,i】的路径终止于非叶节点边(即在该路径上S[i]字符后还有其他字符)而且
下一个字符是S【i+1】(树中已经存在),那么什么也不做。
隐含后缀树的构造,以S=acca为例子(illustration):

Step1:i=1时,根据规则1可知直接创建一个叶子结点1将边标记为a即可;
Step2:i=2时,对于S=ac,根据规则1将c加入1叶子结点的上部;对于S=c,根据规则2创建一个叶子结点2将边标记为c即可;
Step3:i=3时,对于S=acc,根据规则1将c加入1叶子结点的上部;对于S=cc,根据规则1将c加入2叶子结点的上部;
对于S=c,根据规则3不做任何处理;
Step4:i=4时,对于S=acca,根据规则1将a加入1叶子结点的上部;对于S=cca,根据规则1将a加入2叶子结点的上部;
对于S=ca,根据规则2将健一个新的叶子结点3和一个内部结点(边值为a);对于S=c,根据规则3不做任何处理;
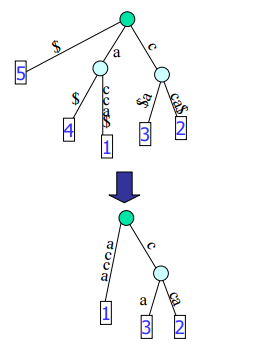
(下图为T3变换为T4的后缀树构建,也就是STEP4所解释的)

说的简单一点就是每一次添加新的后缀前先判断这个后缀在树中是否存在如果不存在则直接创建,如果存在根据其后面的
元素来进行对应的操作1)到达叶子时:直接插入到叶边;2)未到达叶子:创建一个新的叶子结点边标记为S【i+1】 与内
部结点相连;
构建算法:(1、初始化一棵树;2、循环遍历n-1次将树从Ti变换到Ti+1,对于内层循环逐渐更新后缀树通过β=S【j,i】路径
来根据三种规则将S【i+1】添加至树中)

内外层循环时间复杂度为O(n^2),对于每一次的扩展找β的位置时间复杂度为O(|β|),所以总体的时间复杂度为O(n^3);
观察1:规则3一旦使用,其后面的操作均可以省略(减少执行次数,是一个停止规则)
证明:当我们用Rule3扩展β=S【j,i】时,在树中一定存在一个路径以S【i+1】结束路径;所以对于其后面的路径
也一定有以S【i+1】结束路径;(使用Rule3 break即可)
换一种说法就是β=S【j,i】的后缀一定在这颗树中所以一旦在S【j,i】中Rule3那么其其它的后缀也一定满足此条件;
观察2:叶子一旦被创建就不会改变(不会被删除或修改);(一日为叶子终身为叶子)
技巧:对于任意一颗隐含后缀树,其内部结点除了根结点都有一个后缀链;
对于一个内部结点v其路径标签为xα,如果存在其他结点s(v)其路径标签为α,称v指向s(v)的链为后缀链(suffix link)
