线性回归(基于python的小白教程)

线性回归

概念

线性回归是利用数理统计中回归分析，来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法，运用十分广泛。其表达形式为y = w’x+e，e为误差服从均值为0的正态分布。
给出一系列的离散点去拟合符合它的直线

输入	 输出
0.5      5.0
0.6      5.5
0.8      6.0
1.1      6.8
1.4      7.0
...
y = f(x)

预测函数：y = w₀+w₁x
x: 输入
y: 输出
w₀和w₁: 模型参数

所谓模型训练，就是根据已知的x和y，找到最佳的模型参数w₀ 和 w₁，尽可能精确地描述出输入和输出的关系。

5.0 = w₀ + w₁ × 0.5
5.5 = w₀ + w₁ × 0.6

单样本误差：

根据预测函数求出输入为x时的预测值：y’ = w₀ + w₁x，单样本误差为1/2(y’ - y)²。
也就是模型值和精确值之间的差值，但是为了去正值和使数据求导方便以及便于计算，我们取 $\frac{1}{2}(y' - y)^2$

总样本误差：

把所有单样本误差相加即是总样本误差：1/2 Σ(y’ - y)²

损失函数：

loss = 1/2 Σ(w₀ + w₁x - y)²

所以损失函数就是总样本误差关于模型参数的函数，该函数属于三维数学模型，即需要找到一组w₀ w₁使得loss取极小值。

如何求loss的最小值呢？（梯度下降法）

这个在我的上一篇博客中有讲解，有兴趣的可以去阅读一下
点击进入
案例：画图模拟梯度下降的过程

整理训练集数据，自定义梯度下降算法规则，求出w₀ ， w₁ ，绘制回归线。

import numpy as np
import matplotlib.pyplot as mp

w0, w1, losses = [1], [1], []
# 训练次数
times = 1000
# 学习度
lrate = 0.01
epoches = []
train_x = np.array([0.5, 0.6, 0.7, 1.0, 1.2])
train_y = np.array([5.1, 5.3, 6.2, 7.5, 7.8])
for i in range(1, times + 1):
    epoches.append(i)
    loss = (((w0[-1] + w1[-1] * train_x) - train_y) ** 2).sum() / 2
    losses.append(loss)
    print('{:4}> w0={:.8f}, w1={:.8f}, loss={:.8f}'.format(epoches[-1], w0[-1], w1[-1], losses[-1]))
    # 求损失函数关于w0与w1的偏导数，从而更新模型参数
    d0 = (w0[-1] + w1[-1] * train_x - train_y).sum()
    d1 = (train_x * (w0[-1] + w1[-1] * train_x - train_y)).sum()
    # 用梯度下降的方法对模型进行更新
    w0.append(w0[-1] - d0 * lrate)
    w1.append(w1[-1] - d1 * lrate)
pred_y = w0[-1] + w1[-1] * train_x
# 画图
mp.figure('Linear Regression')
mp.title('Linear Regression', fontsize=18)
mp.xlabel('x', fontsize=14)
mp.ylabel('y', fontsize=14)
mp.tick_params(labelsize=10)
mp.grid(linestyle=':')
mp.scatter(train_x, train_y, color='dodgerblue', alpha=0.75, s=40, label='Sample')
mp.plot(train_x, pred_y, c='orangered', label='Regression')
mp.legend()
mp.show()

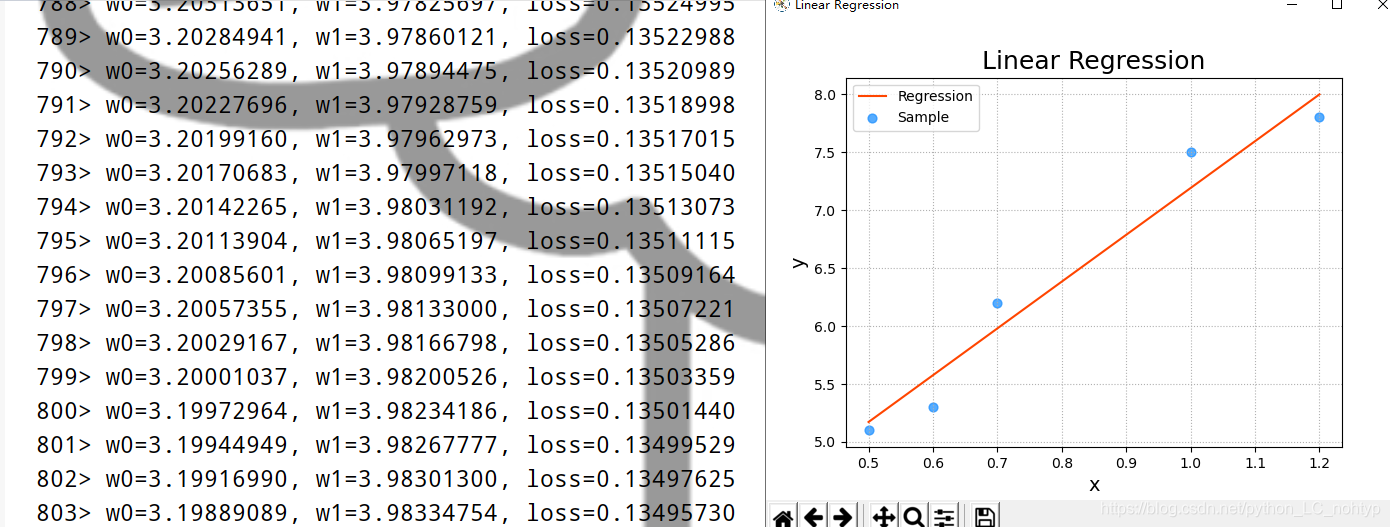
在这里插入图片描述
2. 绘制随着每次梯度下降，w₀，w₁，loss的变化曲线。

w0 = w0[:-1]
w1 = w1[:-1]

mp.figure('Training Progress', facecolor='lightgray')
mp.subplot(311)
mp.title('Training Progress', fontsize=20)
mp.ylabel('w0', fontsize=14)
mp.gca().xaxis.set_major_locator(mp.MultipleLocator(100))
mp.tick_params(labelsize=10)
mp.grid(linestyle=':')
mp.plot(epoches, w0, c='dodgerblue', label='w0')
mp.legend()
mp.subplot(312)
mp.ylabel('w1', fontsize=14)
mp.gca().xaxis.set_major_locator(mp.MultipleLocator(100))
mp.tick_params(labelsize=10)
mp.grid(linestyle=':')
mp.plot(epoches, w1, c='limegreen', label='w1')
mp.legend()

mp.subplot(313)
mp.xlabel('epoch', fontsize=14)
mp.ylabel('loss', fontsize=14)
mp.gca().xaxis.set_major_locator(mp.MultipleLocator(100))
mp.tick_params(labelsize=10)
mp.grid(linestyle=':')
mp.plot(epoches, losses, c='orangered', label='loss')
mp.legend()

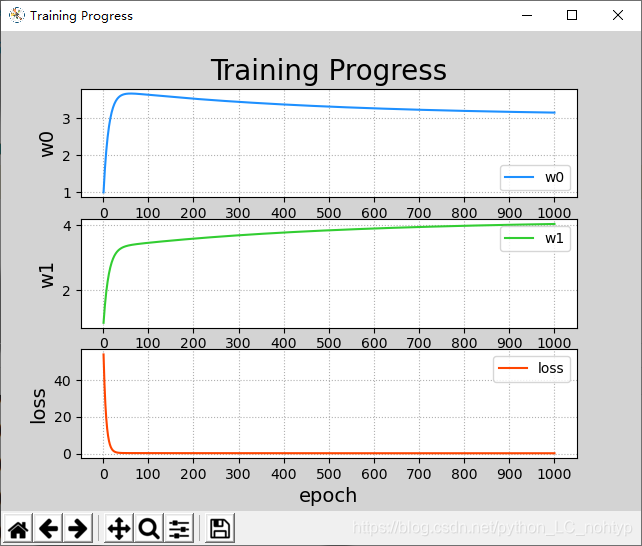
在这里插入图片描述
3. 基于三维曲面绘制梯度下降过程中的每一个点。

"""
线性回归
"""

import numpy as np
import matplotlib.pyplot as mp
import mpl_toolkits.mplot3d as axes3d
w0, w1, losses = [1], [1], []
# 训练次数
times = 1000
# 学习度
lrate = 0.01
epoches = []
train_x = np.array([0.5, 0.6, 0.7, 1.0, 1.2])
train_y = np.array([5.1, 5.3, 6.2, 7.5, 7.8])
for i in range(1, times + 1):
    epoches.append(i)
    loss = (((w0[-1] + w1[-1] * train_x) - train_y) ** 2).sum() / 2
    losses.append(loss)
    print('{:4}> w0={:.8f}, w1={:.8f}, loss={:.8f}'.format(epoches[-1], w0[-1], w1[-1], losses[-1]))
    # 求损失函数关于w0与w1的偏导数，从而更新模型参数
    d0 = (w0[-1] + w1[-1] * train_x - train_y).sum()
    d1 = (train_x * (w0[-1] + w1[-1] * train_x - train_y)).sum()
    # 用梯度下降的方法对模型进行更新
    w0.append(w0[-1] - d0 * lrate)
    w1.append(w1[-1] - d1 * lrate)
pred_y = w0[-1] + w1[-1] * train_x
grid_w0, grid_w1 = np.meshgrid(
    np.linspace(0, 9, 500),
    np.linspace(0, 3.5, 500))

grid_loss = np.zeros_like(grid_w0)
for x, y in zip(train_x, train_y):
    grid_loss += ((grid_w0 + x*grid_w1 - y) ** 2) / 2

mp.figure('Loss Function')
ax = mp.gca(projection='3d')
mp.title('Loss Function', fontsize=20)
ax.set_xlabel('w0', fontsize=14)
ax.set_ylabel('w1', fontsize=14)
ax.set_zlabel('loss', fontsize=14)
ax.plot_surface(grid_w0, grid_w1, grid_loss, rstride=10, cstride=10, cmap='jet')
ax.plot(w0[:-1], w1[:-1], losses, 'o-', c='red', label='BGD')
mp.legend()
mp.show()

在这里插入图片描述
4. 以等高线的方式绘制梯度下降的过程。

mp.figure('Batch Gradient Descent', facecolor='lightgray')
mp.title('Batch Gradient Descent', fontsize=20)
mp.xlabel('x', fontsize=14)
mp.ylabel('y', fontsize=14)
mp.tick_params(labelsize=10)
mp.grid(linestyle=':')
mp.contourf(grid_w0, grid_w1, grid_loss, 10, cmap='jet')
cntr = mp.contour(grid_w0, grid_w1, grid_loss, 10,
                  colors='black', linewidths=0.5)
mp.clabel(cntr, inline_spacing=0.1, fmt='%.2f',
          fontsize=8)
mp.plot(w0, w1, 'o-', c='orangered', label='BGD')
mp.legend()
mp.show()

线性回归 sklearn

线性回归相关API：

股票预测 （只是一个例子，股票并不能这样预测）
均线  obv  趋势线     明天的股价
330  331  333	    345
345  342  339       330
.....

import sklearn.linear_model as lm
# 创建模型
model = lm.LinearRegression()
# 训练模型
# 输入为一个二维数组表示的样本矩阵
# 输出为每个样本最终的结果
model.fit(输入, 输出) # 通过梯度下降法计算模型参数
# 预测输出  
# 输入array是一个二维数组，每一行是一个样本，每一列是一个特征。
result = model.predict(array)

案例：基于线性回归训练single.txt中的训练样本，使用模型预测测试样本。

import numpy as np
import sklearn.linear_model as lm
import matplotlib.pyplot as mp
# 采集数据
x, y = np.loadtxt('../data/single.txt', delimiter=',', usecols=(0,1), unpack=True)
x = x.reshape(-1, 1)
# 创建模型
model = lm.LinearRegression()  # 线性回归
# 训练模型
model.fit(x, y)
# 根据输入预测输出
pred_y = model.predict(x)
mp.figure('Linear Regression', facecolor='lightgray')
mp.title('Linear Regression', fontsize=20)
mp.xlabel('x', fontsize=14)
mp.ylabel('y', fontsize=14)
mp.tick_params(labelsize=10)
mp.grid(linestyle=':')
mp.scatter(x, y, c='dodgerblue', alpha=0.75, s=60, label='Sample')
mp.plot(x, pred_y, c='orangered', label='Regression')
mp.legend()
mp.show()

评估训练结果误差（metrics）

线性回归模型训练完毕后，可以利用测试集评估训练结果误差。sklearn.metrics提供了计算模型误差的几个常用算法：

平均绝对值误差：
就是对所有误差的绝对值取平均数
2.平均平方误差：
对所有误差的平方和求均值
3.中位绝对值误差：
对所有误差的绝对值排个序
4.R2得分：
得到一个（0，1）之间的分值，分数越高，误差越小。

import sklearn.metrics as sm

# 平均绝对值误差：1/m∑|实际输出-预测输出|
sm.mean_absolute_error(y, pred_y)
# 平均平方误差：SQRT(1/mΣ(实际输出-预测输出)^2)
sm.mean_squared_error(y, pred_y)
# 中位绝对值误差：MEDIAN(|实际输出-预测输出|)
sm.median_absolute_error(y, pred_y)
# R2得分，(0,1]区间的分值。分数越高，误差越小。
sm.r2_score(y, pred_y)

案例：在上一个案例中使用sm评估模型误差。

# 平均绝对值误差：1/m∑|实际输出-预测输出|
print(sm.mean_absolute_error(y, pred_y))
# 平均平方误差：SQRT(1/mΣ(实际输出-预测输 出)^2)
print(sm.mean_squared_error(y, pred_y))
# 中位绝对值误差：MEDIAN(|实际输出-预测输出|)
print(sm.median_absolute_error(y, pred_y))
# R2得分，(0,1]区间的分值。分数越高，误差越小。
print(sm.r2_score(y, pred_y))

岭回归

普通线性回归模型使用基于梯度下降的最小二乘法，在最小化损失函数的前提下，寻找最优模型参数，于此过程中，包括少数异常样本在内的全部训练数据都会对最终模型参数造成程度相等的影响，异常值对模型所带来影响无法在训练过程中被识别出来。为此，岭回归在模型迭代过程所依据的损失函数中增加了正则项，以限制模型参数对异常样本的匹配程度，进而提高模型面对多数正常样本的拟合精度。简而言之，就是减小异常样本的干扰。
在这里插入图片描述

import sklearn.linear_model as lm
# 创建模型
model = lm.Ridge(正则强度，fit_intercept=是否训练截距, max_iter=最大迭代次数)
# 训练模型
# 输入为一个二维数组表示的样本矩阵
# 输出为每个样本最终的结果
model.fit(输入, 输出)
# 预测输出  
# 输入array是一个二维数组，每一行是一个样本，每一列是一个特征。
result = model.predict(array)

案例：加载abnormal.txt文件中的数据，基于岭回归算法训练回归模型。

import numpy as np
import sklearn.linear_model as lm
import matplotlib.pyplot as mp
# 采集数据
x, y = np.loadtxt('../data/single.txt', delimiter=',', usecols=(0,1), unpack=True)
x = x.reshape(-1, 1)
# 创建线性回归模型
model = lm.LinearRegression() 
# 训练模型
model.fit(x, y)
# 根据输入预测输出
pred_y1 = model.predict(x)
# 创建岭回归模型
model = lm.Ridge(150, fit_intercept=True, max_iter=10000) 
# 训练模型
model.fit(x, y)
# 根据输入预测输出
pred_y2 = model.predict(x)

mp.figure('Linear & Ridge', facecolor='lightgray')
mp.title('Linear & Ridge', fontsize=20)
mp.xlabel('x', fontsize=14)
mp.ylabel('y', fontsize=14)
mp.tick_params(labelsize=10)
mp.grid(linestyle=':')
mp.scatter(x, y, c='dodgerblue', alpha=0.75,
           s=60, label='Sample')
sorted_indices = x.T[0].argsort()
mp.plot(x[sorted_indices], pred_y1[sorted_indices],
        c='orangered', label='Linear')
mp.plot(x[sorted_indices], pred_y2[sorted_indices],
        c='limegreen', label='Ridge')
mp.legend()
mp.show()

Jupiter-king

发布了62 篇原创文章 · 获赞 33 · 访问量 3500

私信关注