多维高斯分布---【2】

1.一维高斯分布

$\qquad$在介绍二维高斯分布之前我们先介绍一下一维高斯分布的函数图像，如下所示：
$f(x)= \frac{1}{\sqrt{2 \pi}\cdot \delta}\cdot e^{-\frac{{(x-\mu)}^2}{2\delta^2}}$
其中 $\mu$代表均值， $\delta$代表标准差，其图案如下所示：

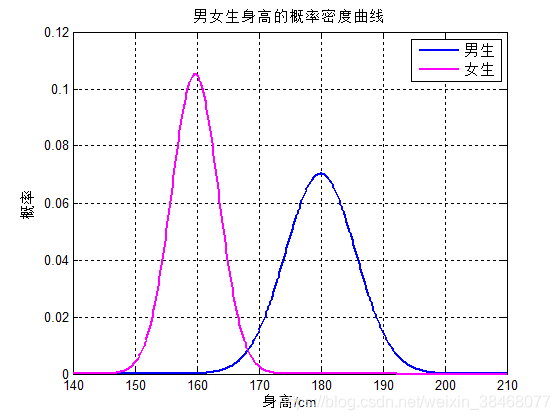
2.二维高斯分布

$\qquad$上边我们介绍了一维的高斯分布，接下来我们介绍一下二维高斯分布，首先贴出其函数表达式，为了简单起见，以下的推导我假设所有变量都是相对独立的，且都服从高斯分布，也就是对于概率分布函数 $f(x_0，x_1,\cdot\cdot\cdot\cdot,x_n)$而言，存在以下等式：
$f(x_0，x_1,\cdot\cdot\cdot\cdot,x_n)=f(x_0)\cdot f(x_1)\cdot\cdot\cdot\cdot f(x_n)$
式中的 $f(x_i)$服从一维的高斯分布
$f(x_i)= \frac{1}{\sqrt{2 \pi}\cdot \delta_i}\cdot e^{-\frac{{(x-\mu_i)}^2}{2\delta_i^2}}$
$\qquad$其中 $\delta_i$和 $\mu_i$是第i个变量的标准差和均值。那当我们来描述二维的高斯分布的话，此处我们的 $n$取值为2。因为 $x_1$和 $x_2$是相互独立的，所以二维的高斯分布函数可以表示为：
$f(x_1,x_2)=f(x_1)\cdot f(x_2)\\ \qquad\qquad\qquad\quad\quad\qquad\qquad\qquad=\frac{1}{\sqrt{2 \pi}\cdot \delta_1}\cdot e^{-\frac{{(x-\mu_1)}^2}{2\delta_1^2}}\cdot \frac{1}{\sqrt{2 \pi}\cdot \delta_2}\cdot e^{-\frac{{(x-\mu_2)}^2}{2\delta_2^2}}\\ \quad\\\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad=\frac{1}{{2 \pi}\cdot \delta_1 \delta_2}\cdot e^{-\frac{[\delta_2^2{(x_1-\mu_1)}^2+\delta_1^2{(x_2-\mu_2)}^2]}{2\delta_1^2\delta_2^2}}$
$\qquad$其二维的高斯分布的图像如下所示：

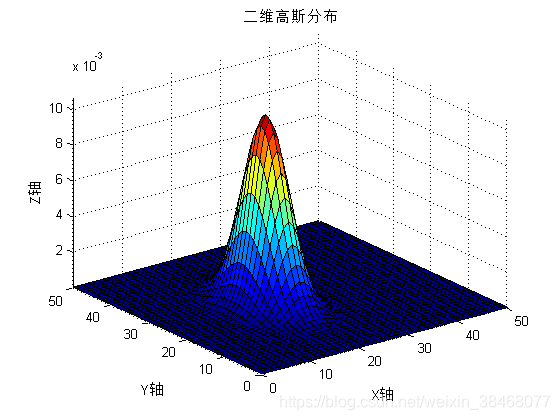
3.多维高斯分布

$\qquad$前边我们介绍了一维的和二维的高斯分布，并且画出了其图像，想必大家也在其它的资料中看到过，通过一维和二维扩展出来的多维的高斯分布的表达公式，就像这样：
$N(\vec{X}\mid\vec{\mu},{\Sigma})=\frac{1}{{(2\pi)}^{\frac{D}{2}}\cdot {\mid \Sigma\mid}^{\frac{1}{2}}}\cdot e^{-\frac{({\vec{X}-\vec{\mu})}^T\cdot{\Sigma^{-1}}\cdot{({\vec{X}-\vec{\mu})}}}{2}}$
$\qquad$式中各个参数代表的意思如下：

1. $\vec{X}$表示维度为D的向量，
2. $\vec{\mu}$是由多个变量 $x_1,x_2,x_3\cdot\cdot\cdot x_n$各自的均值 $u_i$组成的向量，
3. $\Sigma$代表所有向量的协方差矩阵，是一个n维n列的矩阵，
4. $\Sigma^{-1}$代表协方差矩阵的逆，也是一个n维n列的矩阵。

$\qquad$讲到这里感觉对于这个多维的公式中的理解还是不是特别透彻，那么我们可以这么想，既然超过二维的原理上来讲已经算是多维的高斯分布了，那么我们能不能通过第三节的公式推导出第二节的二维高斯分布的函数呢？答案当然是可以：
$\qquad$因为要证明的是二维的情况，所以我们根据上边列出的各个向量分别得到：
$\vec{X}=\left[ \begin{matrix} x_1 \\ x_2 \end{matrix} \right]\ \ \qquad\vec{\mu}=\left[ \begin{matrix} \mu_1 \\ \mu_2 \end{matrix} \right]$
$\qquad$式中 $x_1$和 $x_2$均是长度为n的序列，因为是二维的情况下，所以我们不妨先去求一下协方差矩阵 $\sum$,根据已学知识，我们知道其表达式如下：
$\Sigma=\left[ \begin{matrix} \delta_{11} & \delta_{12}\\ \delta_{21} & \delta_{22} \end{matrix} \right] =\left[ \begin{matrix} DX_1 & Cov(X_1,X_2)\\ Cov(X_2,X_1)& DX_2 \end{matrix} \right] =\left[ \begin{matrix} \delta_{1} ^2& \delta_{12}\\ \delta_{21} & \delta_{2}^2 \end{matrix} \right]$
$\qquad$又因为我们假设 $x_1$和 $x_2$是相互独立的，也就是有 $\delta_{12}=\delta_{21}=0$,于是协方差矩阵即可简化为;
$\Sigma=\left[ \begin{matrix} \delta_{1} ^2& 0\\ 0& \delta_{2}^2 \end{matrix} \right]$
$\qquad$据此我们即可算得协方差的行列式 $\mid \Sigma\mid={\delta_1}^2{\delta_2}^2$,又因为我们选取得是二维高斯分布，所以D取值为2,于是我们将其带入多维高斯分布得左半部分可得;
$\frac{1}{{(2\pi)}^{\frac{D}{2}}\cdot {\mid \Sigma\mid}^{\frac{1}{2}}}=\frac{1}{{(2\pi)}\cdot {\mid{\delta_1}^2{\delta_2}^2\mid}^{\frac{1}{2}}}=\frac{1}{{2 \pi}\cdot \delta_1 \delta_2}$
$\qquad$可见左半部分是和二维分布得函数吻合得的，接下来就进行验证多维分布的右半部分是否与二维的分布相同。
$\qquad$通过上边的部分，我们很轻易即可得到协方差矩阵的逆( $\Sigma^{-1}$)，其值如下:
${\Sigma}^{-1}=\frac{1}{\delta_1^2\delta_2^2}\cdot\left[ \begin{matrix} \delta_{2} ^2& 0\\ 0& \delta_{1}^2 \end{matrix} \right]$
$\qquad$于是我们将我们已知的变量带入即可得到：
$e^{-\frac{({\vec{X}-\vec{\mu})}^T\cdot{\Sigma^{-1}}\cdot{({\vec{X}-\vec{\mu})}}}{2}}=e^{-\frac{1}{2}\cdot \left[ \begin{matrix} x_1-\mu_1& x_2-\mu_2\end{matrix} \right]\cdot\frac{1}{\delta_1^2\delta_2^2}\cdot\left[ \begin{matrix} \delta_{2} ^2& 0\\ 0& \delta_{1}^2 \end{matrix} \right]\cdot\left[ \begin{matrix} x_1-\mu_1\\ x_2-\mu_2\end{matrix} \right]}\\ \qquad \qquad\\\qquad\qquad\qquad\quad=e^{-\frac{1}{2\delta_1^2\delta_2^2}\cdot \left[ \begin{matrix} x_1-\mu_1& x_2-\mu_2\end{matrix} \right]\cdot\left[ \begin{matrix} \delta_{2} ^2& 0\\ 0& \delta_{1}^2 \end{matrix} \right]\cdot\left[ \begin{matrix} x_1-\mu_1\\ x_2-\mu_2\end{matrix} \right]}\\ \qquad \qquad\\\qquad\qquad\qquad\quad=e^{-\frac{1}{2\delta_1^2\delta_2^2}\cdot \left[ \begin{matrix} \delta_2^2\cdot(x_1-\mu_1)& \delta_1^2\cdot(x_2-\mu_2)\end{matrix} \right]\cdot\left[ \begin{matrix} x_1-\mu_1\\ x_2-\mu_2\end{matrix} \right]}\\ \quad \\= e^{-\frac{1}{2\delta_1^2\delta_2^2}\cdot[ \delta_2^2\cdot(x_1-\mu_1)^2+\delta_1^2\cdot(x_2-\mu_2)^2]}$
$\qquad$好了通过上边公式的推导，我们可以看到通过多维情况下我们可以完整的得出二维情况下的高斯分布表达式。

4.心声

$\qquad$原理虽简单，但还是在纸上详细推导一遍比较好，不要眼高手低~~
加油呀，各位~。