[多项式学习笔记1]拉格朗日插值定理

[多项式学习笔记1]拉格朗日插值定理

算法简介

拉格朗日插值法是以法国18世纪数学家约瑟夫·拉格朗日命名的一种多项式插值方法。

适用问题

拉格朗日插值定理主要是用来解决下面这样的问题：

给出 n 个点 (xi,yi)（保证 xi 互不相同），要求找出一个过所有点的多项式函数 f(x)。 

显然最直观的方法是采用高斯消元，但高斯消元时间复杂度较高且有精度误差

这时候就可以考虑用拉格朗日插值定理了

算法流程

显然对于每个点，我们尝试找出一个函数 fi(x)，使得 fi(xi) = yi， 并且对于其他的所有横坐标 xj(j!=i) 有 fi(xj) = 0。那么把 n 个 fi(x) 加起来就能得到要求的函数 f(x) 了

可以推出式子：

 时间复杂度 O(n^2)

代码（luogu模板）

#include<bits/stdc++.h>

#define ll long long

using namespace std;

inline ll read()
{
    ll f = 1 , x = 0;
    char ch;
    do
    {
        ch = getchar();
        if(ch=='-') f=-1;
    } while(ch<'0'||ch>'9');
    do
    {
        x=(x<<3) + (x<<1) + ch - '0';
        ch = getchar();
    }while(ch>='0'&&ch<='9');
    return f*x;
}

const int MAXN = 2000 + 10;
const ll MOD = 998244353;

inline ll Pow(ll a,ll b)

{
    ll ans = 1,mul = a;
    while(b)

    {
        if(b&1) ans = (ans * mul) % MOD;
        mul = (mul * mul)%MOD;

        b>>=1;

    }
    return ans;
}

inline ll inv(ll a)
{
    return Pow(a,MOD-2);
}

ll n,k;
ll x[MAXN],y[MAXN];
ll ans;

int main()
{
    n = read(),k = read();
    for(int i=1;i<=n;i++) x[i] = read(),y[i] = read();
    for(int i=1;i<=n;i++)
    {
        ll res1 = y[i] % MOD;
        ll res2 = 1;
        for(int j=1;j<=n;j++)

        {
            if(i == j) continue;
            res1 = (res1 * (k - x[j]%MOD + MOD)%MOD)%MOD;
            res2 = (res2 * ((x[i] - x[j]%MOD + MOD)%MOD))%MOD;
        }
        ans = (ans + (res1 * inv(res2) % MOD)%MOD) % MOD;
    }
    cout << ans << endl;
}

拉格朗日插值定理的扩展

• 当X取值连续时，可以通过记录前缀和和后缀和做到线性时间复杂度
• 重心拉格朗日插值定理：

拉格朗日插值法的公式结构整齐紧凑，在理论分析中十分方便，然而在计算中，当插值点增加或减少一个时，所对应的基本多项式就需要全部重新计算，
于是整个公式都会变化，非常繁琐。这时可以用重心拉格朗日插值法

　　将拉格朗日插值定理变形为：

　　

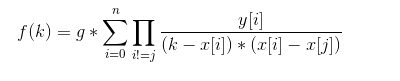
扫描二维码关注公众号，回复： 9427526 查看本文章

　　其中 g =

　　　　　　　　 

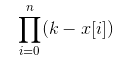
　　然后另 Ti =

　　　　　　　　 

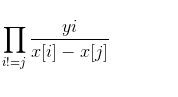
　　当增加一个点时直接增加ti即可