数值分析Java实现——拉格朗日（Lagrange）插值多项式&牛顿（Newton）插值多项式&线性拟合数据

插值方法——代数插值

实际的问题中碰到的函数是各种各样的，有的表达式比较复杂如：
$f\left(x\right)=\sqrt{\sin x}\frac{\ln x}x$
甚至有些根本无法得出解析解，只能得到一些离散的数据点或者一些点的导数值。这样一来研究原来的函数就显得比较吃力。而插值方法就是为了解决这一问题的诞生的。我们通过对有限个点数据进行分析，并由此得到与原函数近似的一个函数，由得到的函数来代替原函数进行研究。选用不同的插值方式得到的逼近效果不一样。由于考虑到计算机的运算特点，选用结构简单，对计算机友好的代数多项式来作为近似函数的基本形式，这种方式又叫代数插值。

Source codes address:Source codes in github

问题引入

研究函数 $f\left(x\right)=\sin x.$在给定的有限数据的基础上，利用不同的插值方法得到对应的插值多项式，并估计给定的点 $x_0\mathrm{处的函数值}f(x_0).$

拉格朗日（Lagrange）插值多项式

1.根据给定的数据求出拉格朗日的插值基函数: $l_k{\left(x\right)}=\prod_{j=0}^n\frac{x-x_j}{x_k-x_j}(j≠k).$
2.利用给定的函数值与基函数结合并求出累加和即得到拉格朗日插值多项式，并根据此多项式计算得到 $f(x_0)$的估计值
$L_n(x)=\sum_{k=0}^nl_k\left(x\right)y_k.$

具体算法框图：

Source codes

源程序代码：
/**
 * @Classname LagrangeTool
 * @Description the functions of the Lagrange methods
 * @Date 2020/4/22 10:55
 * @Created by Jason
 * 用拉格朗日（Lagrange）插值多项式计算f(x0)的近似值
 * 以sin(x)为研究函数
 */
public class LagrangeTool {
//    real values
    private double f(double x) {
        return Math.sin(x);
    }
//    获取Lagrange的近似估计值
    public double getEstimates(double x0){
        List<Double> xi = InitDataSource.getInitValues();
        int length = xi.size();
        double estimates = 0;
        for (int k = 0 ; k < length ; k++ ) {
            estimates += f(xi.get(k))*Lk(x0,k,xi);
        }
        return estimates;
    }
    private static double Lk(double x,int k,List<Double> xi) {
        double value = 1.0;
        for (int j = 0; j < xi.size(); j++) {
            if (j != k) {
                value *= (x - xi.get(j)) / (xi.get(k) - xi.get(j));
            }
        }
        return value;
    }
}
public class Test {
    public static void main(String[] args) {
        LagrangeTool lagrangeTool = new LagrangeTool() ;
        System.out.println("研究函数f(x)=sin(x),请输入点x0的值：");
        Scanner scanner = new Scanner(System.in);
        double x0 = scanner.nextDouble();
        double value = lagrangeTool.getEstimates(x0);
        System.out.println("用拉格朗日（Lagrange）插值多项式计算f("+ x0 +")的近似值为：" + value);
        System.out.println( "f("+ x0 +")精确值为：" + Math.sin(x0));
        System.out.println("误差：" + Math.abs(Math.sin(x0) - value));
    }
}

运行结果图：

数据分析

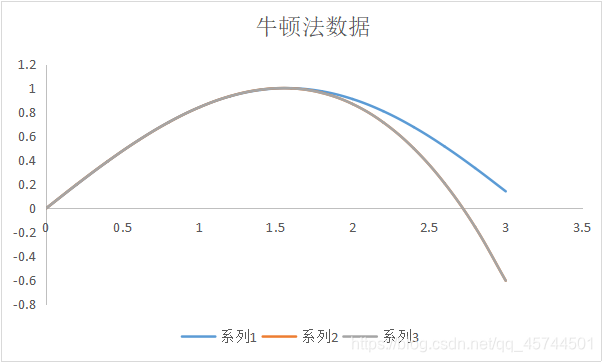
计算结果数据如下，第一列为 $x_0$的取值，第二列为精确值，第三列为拉格朗日估计值。为了方便观察数据，绘制了对应的图像：系列1为精确图像，系列2为插值函数图像。

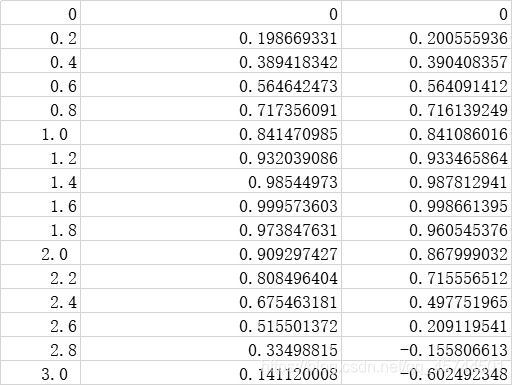
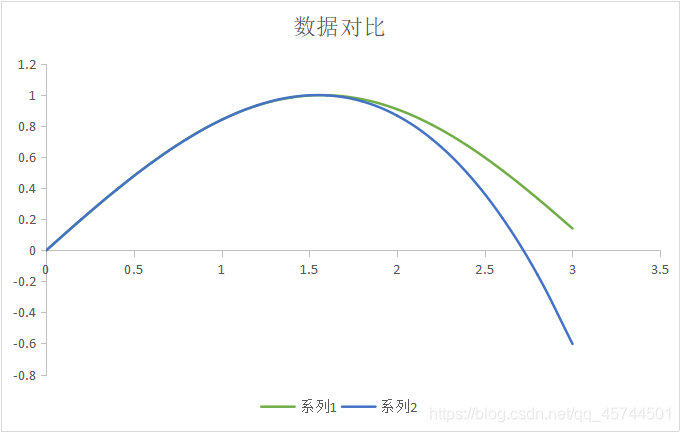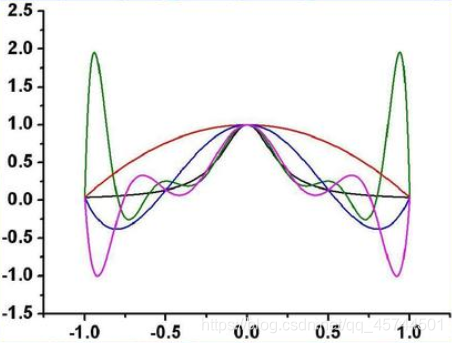
可见插值函数的图像在最初的区间 $x_0\in\left[0,\frac\pi2\right].$中有较好的逼近效果，即是内插的逼近效果好。但是到后面可以发现：其与实际的函数图像的误差开始拉大，一方面是由于外插。其实随着区间扩大，或者数据点的增多，出现高次插值，很可能出现龙格现象，即是插值函数在两端激烈震荡。

牛顿（Newton）插值值多项式

牛顿 $(Newton)$插值是一个具有承袭性的插值公式。

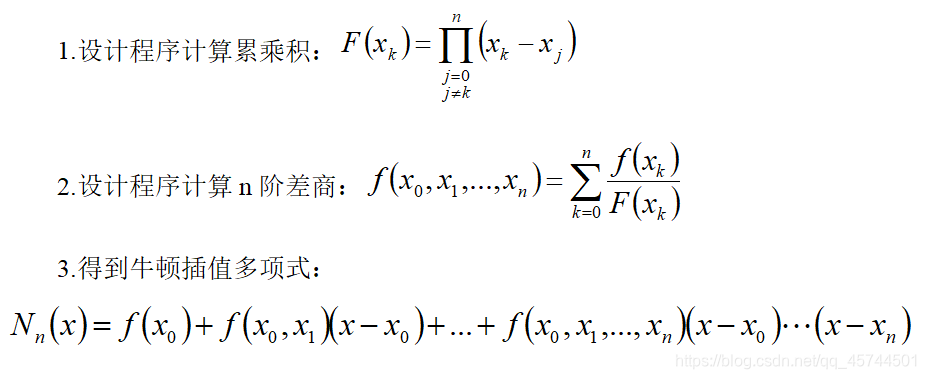
具体算法框图：

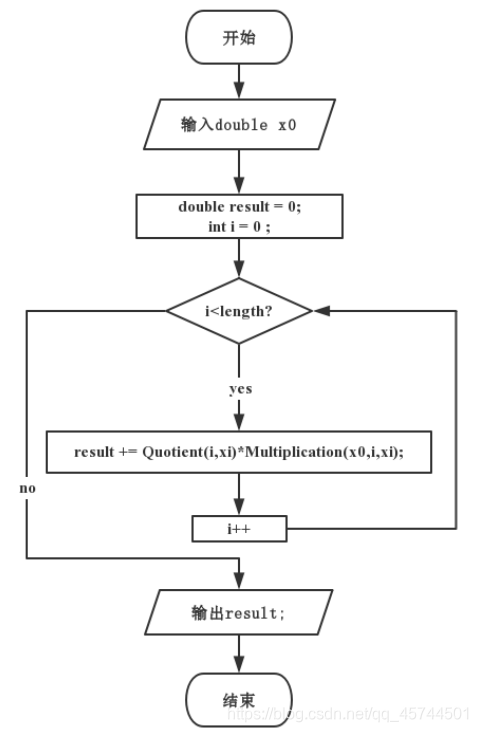
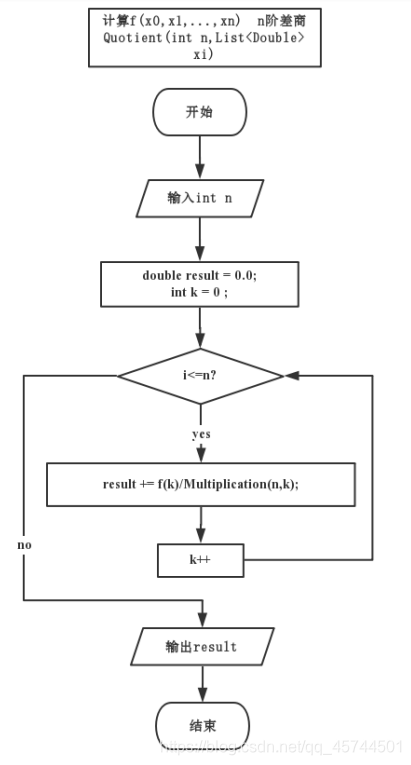
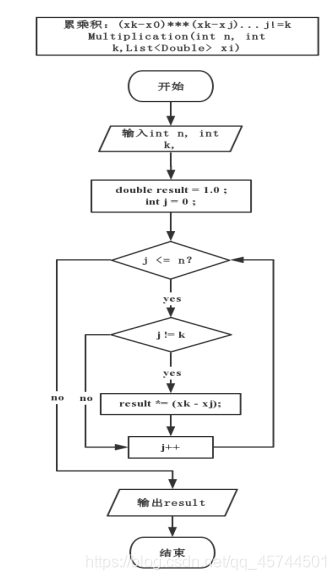
Source codes

/**
 * @Classname NewtonTool
 * @Description TODO
 * @Date 2020/4/22 15:13
 * @Created by ASUS
 */
public class NewtonTool {

    public NewtonTool() {}

    private static double f(double x) {
        return Math.sin(x);
    }
//  累乘积：(x-x0)***(x-xn)
    private static double Multiplication(double x,int n,List<Double> xi) {
        double result = 1.0 ;
        for (int i = 0 ; i < n; i++ ) {
            result *= (x - xi.get(i));
        }
        return result;
    }
    //  累乘积：(xk-x0)***(xk-xj)...j!=k
    private static double Multiplication(int n, int k,List<Double> xi) {
        double result = 1.0 ;
        for (int j = 0 ; j <= n; j++ ) {
            if(j != k){
                result *= (xi.get(k) - xi.get(j));
            }
        }
        return result;
    }
//  f(x0,x1,...,xn)  n阶差商
    private static double Quotient(int n,List<Double> xi) {
        double result = 0.0;
        for (int k = 0 ; k <= n ; k++) {
            result += f(xi.get(k))/Multiplication(n,k,xi);
        }
        return result;
    }
//  得到估计值
    public static double getEstimates(double x0) {
        double result = 0;
        List<Double> xi = InitDataSource.getInitValues();
        for (int i = 0 ; i < xi.size() ; i++ ) {
            result += Quotient(i,xi)*Multiplication(x0,i,xi);
        }
        return result;
    }
}

运行截图

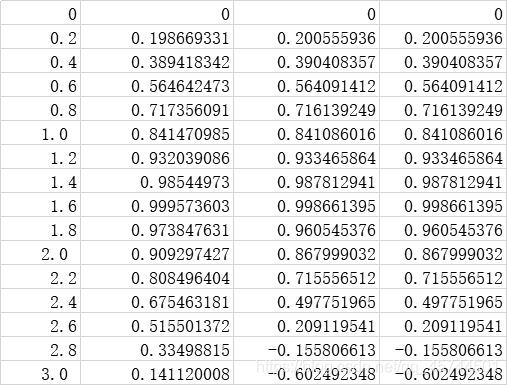
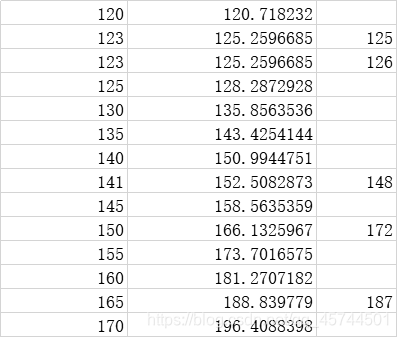
数据分析

对于同一组初始数据得到的数据结果是一致的。

线性拟合数据

理论推导：

初始数据

算法框图

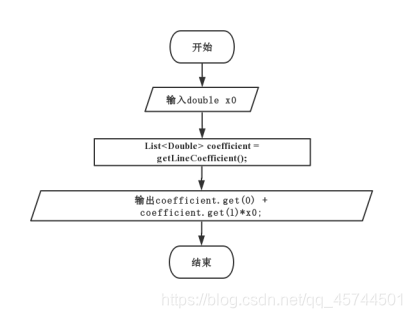
变量声明

N = y.size();//样本的数量
F = getSumOf(IntegrateData(x,y));//计算得到值： $\sum x_iy_i$
T = getSumOf(y);//计算得到值： $\sum y_i$
S = getSumOf(x);//计算得到值： $\sum x_i$
K = getSumOf(IntegrateData(x,x));//计算得到值： $\sum x_i^2$

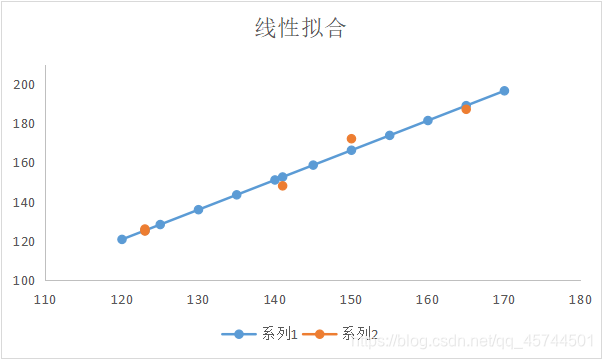
拟合数据

拟合效果图

运行截图

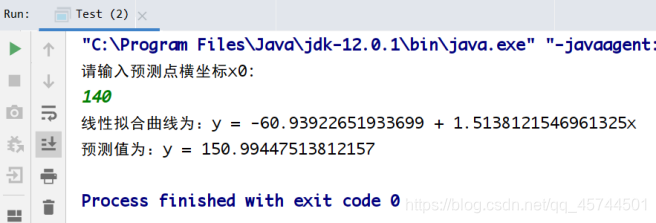
Source codes

/**
 * @Classname LinearFitting
 * @Description TODO
 * @Date 2020/4/22 16:52
 * @Created by ASUS
 */
public class LinearFitting {

    private static Double [] data_x = {165.0,123.0,150.0,123.0,141.0} ;
    private static Double [] data_y = {187.0,126.0,172.0,125.0,148.0} ;

    private static List<Double> x = Arrays.asList(data_x);
    private static List<Double> y = Arrays.asList(data_y);

//    输入集合数据，并累计求和
    private static double getSumOf(List<Double> datas) {
        double restlt = 0.0;
        for (int i = 0 ; i < datas.size() ; i++ ) {
            restlt += datas.get(i);
        }
        return restlt;
    }
//  整合数据项
    private static List<Double> IntegrateData(List<Double> x,List<Double> y) {
        if(x.size() != y.size()){
            throw new RuntimeException("传入的两个数据集合长度不一致") ;
        }
        List<Double> res = new ArrayList<>() ;
        for (int i = 0 ; i < x.size(); i++ ) {
            res.add(x.get(i)*y.get(i));
        }
        return res;
    }
//  返回得到的拟合曲线 y = a + bx;的a与b的值，存在集合中
    public static List<Double> getLineCoefficient() {
        double a,b;
        b = getB();
        a = getA(b);
        List<Double> res = new ArrayList<>();
        res.add(a);
        res.add(b);
//        System.out.println("线性拟合曲线为：y = " +
//                res.get(0) + " + " + res.get(1) + "x");
        return res;
    }
//  获得系数a
    private static double getA(double b) {
        double N,T,S;
        N = y.size();
        T = getSumOf(y);
        S = getSumOf(x);
        return (T - b*S)/N;
    }
//  获得系数b
    private static double getB() {
        double b =0;
        double N,F,T,S,K;
        N = y.size();
        F = getSumOf(IntegrateData(x,y));
        T = getSumOf(y);
        S = getSumOf(x);
        K = getSumOf(IntegrateData(x,x));
        b = (N*F - T*S)/(N*K - S*S);
        return b;
    }

    //  得到估计值
    public static double getEstimates(double x0) {
        List<Double> coefficient = getLineCoefficient();
        return coefficient.get(0) + coefficient.get(1)*x0;
    }
}