递归与线性对比
当n的值从1万增加到10万时,第二个程序会由于开辟的内存过大,导致内存溢出,程序异常终止。空间复杂度过高。

#include <stdio.h>
#include <stdlib.h>
#include <math.h>
int main()
{
int a=10;
PrintN1(a);
printf("\n");
PrintN2(a);
return 0;
}
void PrintN1(int n)//线性执行
{
int i;
for(i=1;i<=n;i++)
{
printf("%d\t",i);
}
}
void PrintN2(int n)//递归执行
{
if(n>0)
{
PrintN2(n-1);
printf("%d\t",n);
}
}
秦九昭算法和普通算法
明显少了一个量级,秦九昭算法的速度是:O(n),一般的多项式计算速度是O(n^2)。速度变快!我国数学家真厉害!!
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
int main()
{
int n=10000;
int a[3]={1,2,3};
int x=2;
printf("%d\t%d",f1(n,a,x),f2(n,a,x));
return 0;
}
//计算一元多项式
int f1(int n,int a[],int x)
{
//计算阶数为n,系数为a[]....a[n]的多项式在x点的值
int i;
int p=a[0];
for(i=1;i<=n;i++)
{
p+=a[i]*pow(x,i);
}
return p;
}
//秦九韶算法:f(x)=a0+x(a1+x(...(an-1+x(an))))
int f2(int n,int a[],int x)
{
int i;
int p=a[n];
for(i=n;i>0;i--)
p=a[i-1]+x*p;
return p;
}
算法速度对比:
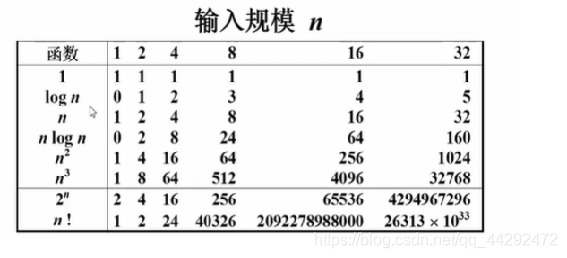
在计算机内只需要关注乘的次数,不必在意加法,可知log(n)运行速度最快!我们在使用时,最好将算法的速度改进到log(n)!
选择排序:
void SelectSort(int a[],int n)//需要排序的数组和其中存的数字个数
{
int i,j,mix,temp;
for(i=0;i<n-1;i++)//循环n-1次即可排序完成
{
mix=i;//假设最小元的下标
for(j=i+1;j<n;j++)
{
if(a[j]<a[mix])//找到比mix还小的数字的话,记住其下标
mix=j;
}
if(i!=mix)//如果有就就交换,找到本轮i值对应的最小值,并进入下一i的确定
{
temp=a[i];
a[i]=a[mix];
a[mix]=temp;
}
}
}
算法复杂度:
(1)空间复杂度S(n)——根据算法写成的程序在执行时所占用存储单元的长度。这个长度往往和输入的规模n有关。空间复杂度过高的算法可能导致使用的内存超限,造成程序非正常中断。
(2)时间复杂度T(n)——根据算法写的程序在执行时所花费时间的长度,这个长度往往也与输入数据的规模n有关。时间复杂度过高的低效率算法可能导致我们在有生之年都等不到程序运行结果
应用实例:最大子列和问题
给定n个整数序列{a1,a2,a3…an},求函数f(i,j)=max{0,Σk<-i to j ak}的最大值。
例如:{-2,11,-4,13,-5,-2},其最大子列位{11,-4,13},和为20。
代码一:
int MaxSubseqSuml(int List[],int N)
{
int i,j,k;
int ThisSum,MaxSum=0;
for(i=0;i<N;i++)//i是子列最左端位置
{
for(j=i;j<N;j++)//j是子列最右端位置
{
ThisSum=0;//从List[i]-->List[j]的子列和
for(k=i;k<=j;k++)
ThisSum+=List[k];//从i加到j
if(ThisSum>MaxSum)//如果这个子列和比目前最大值大,就更新最大值
MaxSum=ThisSum;
}//j层循环结束
}//i层循环结束
return MaxSum;
}
这个代码的时间复杂度是由3层for()循环所决定。
T(N)=ΣΣΣ1=O(N^3)
不难发现最内层有大量重复的代码,是最大的浪费点。因为当固定i,当j增大了1以后,k循环要重新从i加到j。事实上第j-1步的计算完全可以存下来,第j步只要在此基础上累加一个List[ j ]就可以了。没有必要再从头加起!
下面我们将里面部分中间值采用穷举。得到代码二。
代码二:
int MaxSubseqSum2(int List[],int N)
{
int i,j;
int ThisSum,MaxSum=0;
for(i=0;i<N;i++)//左端
{
ThisSum=0;
for(j=i;j<N;j++)//右端
{//对于相同的i,不同的j,只要在j-1次循环的基础之上累加1项即可
ThisSum+=List[j];
if(ThisSum>MaxSum)
MaxSum=ThisSum;
}//j循环结束
}//i循环结束
return MaxSum;
}
这次将3个for()循环降成2个for()循环,时间复杂度得到一定改善。
T(n)=O(n^2)。
但这仍然不是最快的算法,下面我们将使用分而治之的方法来将原问题进行拆解成若干个小问题,然后再将其结果进行合并,使用递归的话十分方便。
将原始序列一分为二,那么最大子列或者在左半边,或者在右半边,或者是横跨中分线的一段。
最后将三段的最大值进行合并,即:Smax=max{ S左,S中,S右 }。
代码三:
int Max3(int A, int B, int C)
{
return A>B ? (A>C ? A:C):(B >C ? B:C);//嵌套版三目运算求最大值
}
int DivideAndConquer(int List[], int left, int right)
{//分治法求List[left]--->List[right]的最大子列和
int MaxLeftSum,MaxRightSum;//存放左右子问题的解
int MaxLeftBorderSum,MaxRightBorderSum;//存放跨分界的结果
int LeftBorderSum,RightBorderSum;
int center,i;
if(left==right)//递归终止条件,子列只有一个数字
{
if(List[left]>0) return List[left];
else return 0;
}
//下面是“分”的过程
center=(left+right)/2;//找到中分点
//递归求的两边子列的最大和
MaxLeftSum=DivideAndConquer(List,left,center);
MaxRightSum=DivideAndConquer(List,center+1,right);
//下面求跨分界的最大子列和
MaxLeftBorderSum=0;LeftBorderSum=0;
for(i=center;i>=left;i--)
{
LeftBorderSum+=List[i];
if(LeftBorderSum>MaxLeftBorderSum)
MaxLeftBorderSum=LeftBorderSum;
}//左边扫描结束
MaxRightBorderSum=0;RightBorderSum=0;
for(i=center+1;i<right;i++)//从中线向右扫描
{
RightBorderSum+=List[i];
if(RightBorderSum>MaxRightBorderSum)
MaxRightBorderSum=RightBorderSum;
}//右边扫描结束
//下面返回“治”的结果
return Max3(MaxLeftSum,MaxRightSum,MaxLeftBorderSum+MaxRightBorderSum);
}
int MaxSubseqSum3(int List[],int N)
{//保持与前两种算法相同的函数接口
return DivideAndConquer(List,0,N-1);
}
解决问题的核心函数是DivideAndConquer——分而治之,但是作为专业的程序员,还要在拥有相同功能的同是,不改变原有的接口,若记这个代码的时间复杂度位:T(N),则函数进行分的复杂度为:2T(N/2),因为我们解决了两个长度减半的子问题,所以在O(N)时间完成。其他步骤都只需要O(1)时间。
综上分析得递推式:
T(1)=O(1);
T(N)=2T(N/2)+O(N)
=2[2T(N/2)/2+O(N/2)]+O(N)=22T(N/22)+2O(N)
=…=2kT(N/2k)+kO(N)
当我们不断对分,直到N/2^k^=1,即2^k^=N时,T(N)=N*T(1)+logN*O(N)=O(NlogN)。
由图可知其速度将大于O(n^2^).
但这仍然不是最快的算法!下面讲一种在线处理的算法,在线就是每输入一个数据经行即时处理,得到的结果对于已读入的所有数据都成立。即在任何一个地方终止程序,算法都能正确给出当前的解。
前面三种给出的都是必须等所有的N个整数读取并存储后才可以进行计算!下面将进行的时不用存储,就可以即时计算任何时刻的最大子列和。
该算法的核心是基于下面的事实:如果整数序列{a1,a2,…an}的最大和子列是{ai,ai+a,…aj},那么必定有Σi->l ak>=0对于任意的i<=l<=j成立。因此,一旦发现当前子列和为负数,则重新开始考察一个新的子列。
代码四:
int MaxSubseqSum4(int List[],int N)
{
int i;
int ThisSum,MaxSum;
ThisSum=MaxSum=0;
for(i=0;i<N;i++)
{
ThisSum+=List[i];
if(ThisSum>MaxSum)
MaxSum=ThisSum;
else if(ThisSum<0)
ThisSum=0;
}
return MaxSum;
}
程序运行流程图:
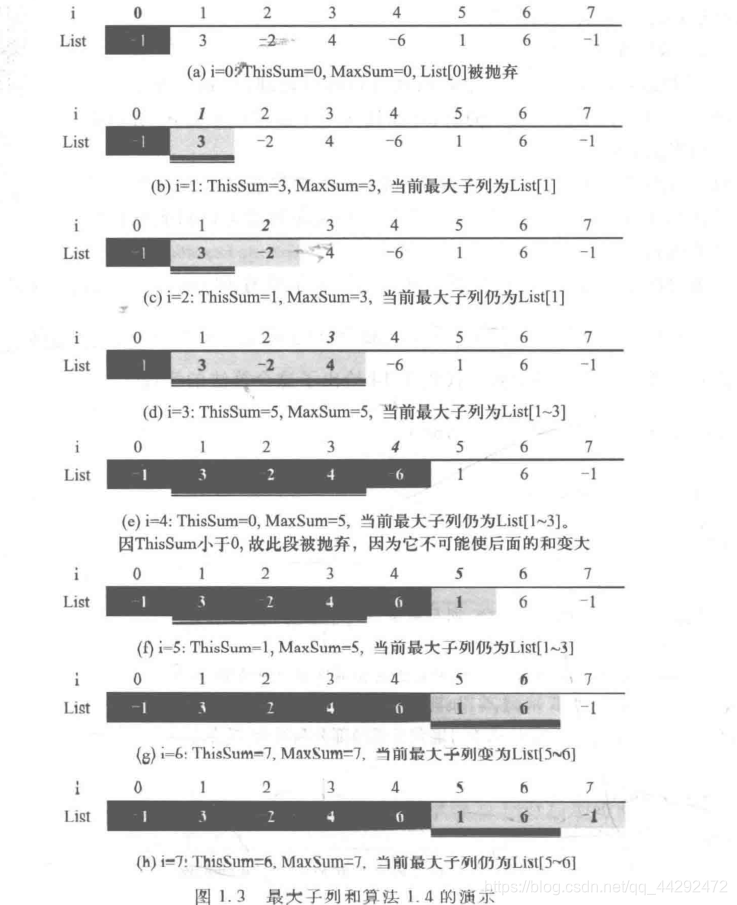
这种在线处理的方式,不需要将数据存储起来,我们只需要一个一个读入,同时,一个一个处理即可,处理过后的数据也没有必要存起来。整个算法只把数据扫描了一遍,应该是最快的算法了!!
本章小结:
本章介绍了两个重要概念:“数据结构”和“算法”。
数据结构:包括数据对象集以及它们在计算机中的组织方式,即他们的逻辑结构和物理结构,同时还包括数据对象集相关联的操作集,以及实现这些操作的高效算法。抽象数据型是用来描述数据结构的重要类型。
算法:是解决问题步骤的有限集合,通常用某一种计算机语言进行伪码描述。我们用时间复杂度和空间复杂度来衡量算法的优劣,用渐进表示法分析算法复杂度的增长趋势。
本章算法程序原码:
#include <stdio.h>
void SelectSort(int a[],int n);//选择排序
int MaxSubseqSuml(int List[],int N);//求最大子列和
int MaxSubseqSum2(int List[],int N);
int MaxSubseqSum3(int List[],int N);
int MaxSubseqSum4(int List[],int N);
int Max3(int A, int B, int C);
int DivideAndConquer(int List[], int left, int rigth);
int main()
{
int n,i;
int a[10];
scanf("%d",&n);
for(i=0;i<n;i++)
{
scanf("%d",&a[i]);
}
//求最大子列和问题
int maxsub=MaxSubseqSuml(a,n);
int maxsub2=MaxSubseqSum2(a,n);
int maxsub3=MaxSubseqSum3(a,n);
int maxsub4=MaxSubseqSum4(a,n);
printf("%d\n%d\n%d\n%d\n",maxsub,maxsub2,maxsub3,maxsub4);
SelectSort(a,n);
for(i=0;i<n;i++)
{
printf("%d\t",a[i]);
}
return 0;
}
void SelectSort(int a[],int n)//需要排序的数组和其中存的数字个数
{
int i,j,mix,temp;
for(i=0;i<n-1;i++)//循环n-1次即可排序完成
{
mix=i;//假设最小元的下标
for(j=i+1;j<n;j++)
{
if(a[j]<a[mix])//找到比mix还小的数字的话,记住其下标
mix=j;
}
if(i!=mix)//如果有就就交换,找到本轮i值对应的最小值,并进入下一i的确定
{
temp=a[i];
a[i]=a[mix];
a[mix]=temp;
}
}
}
int MaxSubseqSuml(int List[],int N)
{
int i,j,k;
int ThisSum,MaxSum=0;
for(i=0;i<N;i++)//i是子列最左端位置
{
for(j=i;j<N;j++)//j是子列最右端位置
{
ThisSum=0;//从List[i]-->List[j]的子列和
for(k=i;k<=j;k++)
ThisSum+=List[k];//从i加到j
if(ThisSum>MaxSum)//如果这个子列和比目前最大值大,就更新最大值
MaxSum=ThisSum;
}//j层循环结束
}//i层循环结束
return MaxSum;
}
int MaxSubseqSum2(int List[],int N)
{
int i,j;
int ThisSum,MaxSum=0;
for(i=0;i<N;i++)//左端
{
ThisSum=0;
for(j=i;j<N;j++)//右端
{//对于相同的i,不同的j,只要在j-1次循环的基础之上累加1项即可
ThisSum+=List[j];
if(ThisSum>MaxSum)
MaxSum=ThisSum;
}//j循环结束
}//i循环结束
return MaxSum;
}
int Max3(int A, int B, int C)
{
return A>B ? (A>C ? A:C):(B >C ? B:C);//嵌套版三目运算求最大值
}
int DivideAndConquer(int List[], int left, int right)
{//分治法求List[left]--->List[right]的最大子列和
int MaxLeftSum,MaxRightSum;//存放左右子问题的解
int MaxLeftBorderSum,MaxRightBorderSum;//存放跨分界的结果
int LeftBorderSum,RightBorderSum;
int center,i;
if(left==right)//递归终止条件,子列只有一个数字
{
if(List[left]>0) return List[left];
else return 0;
}
//下面是“分”的过程
center=(left+right)/2;//找到中分点
//递归求的两边子列的最大和
MaxLeftSum=DivideAndConquer(List,left,center);
MaxRightSum=DivideAndConquer(List,center+1,right);
//下面求跨分界的最大子列和
MaxLeftBorderSum=0;LeftBorderSum=0;
for(i=center;i>=left;i--)
{
LeftBorderSum+=List[i];
if(LeftBorderSum>MaxLeftBorderSum)
MaxLeftBorderSum=LeftBorderSum;
}//左边扫描结束
MaxRightBorderSum=0;RightBorderSum=0;
for(i=center+1;i<right;i++)//从中线向右扫描
{
RightBorderSum+=List[i];
if(RightBorderSum>MaxRightBorderSum)
MaxRightBorderSum=RightBorderSum;
}//右边扫描结束
//下面返回“治”的结果
return Max3(MaxLeftSum,MaxRightSum,MaxLeftBorderSum+MaxRightBorderSum);
}
int MaxSubseqSum3(int List[],int N)
{//保持与前两种算法相同的函数接口
return DivideAndConquer(List,0,N-1);
}
int MaxSubseqSum4(int List[],int N)
{
int i;
int ThisSum,MaxSum;
ThisSum=MaxSum=0;
for(i=0;i<N;i++)
{
ThisSum+=List[i];
if(ThisSum>MaxSum)
MaxSum=ThisSum;
else if(ThisSum<0)
ThisSum=0;
}
return MaxSum;
}
