深度通信网络专栏（2）|自编码器：无信道模型的通信系统端到端学习

本文地址：https://arxiv.org/abs/1804.02276

前言

深度通信网络专栏|自编码器: 整理2018-2019年使用神经网络实现通信系统自编码器的论文，一点拙见，如有偏颇，望不吝赐教，顺颂时祺。

文章中心思想

原来的自编码器采用监督学习，需要一个可微分的信道模型，信道函数必须已知，这种情况下训练出来的模型，如要应用，实际信道应该与训练时的信道相近。为保证性能，现常常采用线下训练，线上微调的方式（即应用时，接收端根据接收的数据微调模型参数），这带来的缺点是发送端不可再微调，得到的仅是次优解。

事实上，信道对我们而言只是一个黑匣子，我们只能观测输入输出，我们并不总能得到一个可微的信道模型。为解决这一问题，本文作者提出了迭代优化接收端和发送端的自编码器，其中接收端使用监督学习，发送端使用强化学习。这一方法中，发送端的强化学习是基于损失函数的梯度来优化，使用policy learning，无需知道信道梯度。由于这一方法不需要知道信道模型，因此能在实际信道中直接训练。

与将发送端、信道、接收端看作一个NN的全监督学习算法对比，本文提出的迭代算法能达到几乎一样的性能，且在瑞利信道下收敛更快。这一结果表明：信道模型和信道传递函数不是必要的，自编码器可以仅仅根据观测数据进行训练。

原文结论：Our results are a first step towards learning of communications systems over any type of channel without prior assumptions

一点说明

• 为了使读者更好地理解发送端使用强化学习训练避免了信道函数未知的情况，这里先做一个粗浅的说明
• policy learning参考： ①深入浅出介绍策略梯度 - IBM ②策略梯度

上图为强化学习的基本构成，在本文中，state对应输入数据m，reward对应接收端反馈的损失loss，agent对应输入端神经网络，action对应输入到信道的码字，environment对应信道-参数固定的接收端神经网络（注：在训练发送端时，接收端神经网络参数固定）。在迭代训练中，下一状态依旧为S_t+1依旧为提供给神经网络的输入m。也就是说，每一组训练数据会迭代N次，直到满足迭代终止条件，再输入给神经网络一组新的数据进行训练。

从上面的说明可以看出，发送神经网络的训练与environment的具体形式无关，也就是说我不需要知道信道的函数，只要你给我reward和state，我的agent就可以给出对应的action，使得reward最大（loss最小）。那么问题就是，发送端的参数是如何更新的？（如果使用我们熟知的监督学习，loss直接对θt求导来更新θt，必然涉及信道函数），这就引入了policy learning：

从上图（截图来自策略梯度）可以看出，策略目标函数是奖励与策略函数的乘积（大体上先这样理解），这里奖励对应于接收端反馈的loss，对于每一次训练是一个具体的数值，而策略函数可以暂时粗浅地理解为我们要训练的输入端神经网络（要学习的编码方式即是策略）。因此根据策略目标函数更新策略函数的参数只与策略函数有关，并不涉及信道函数。

全文概述

系统模型

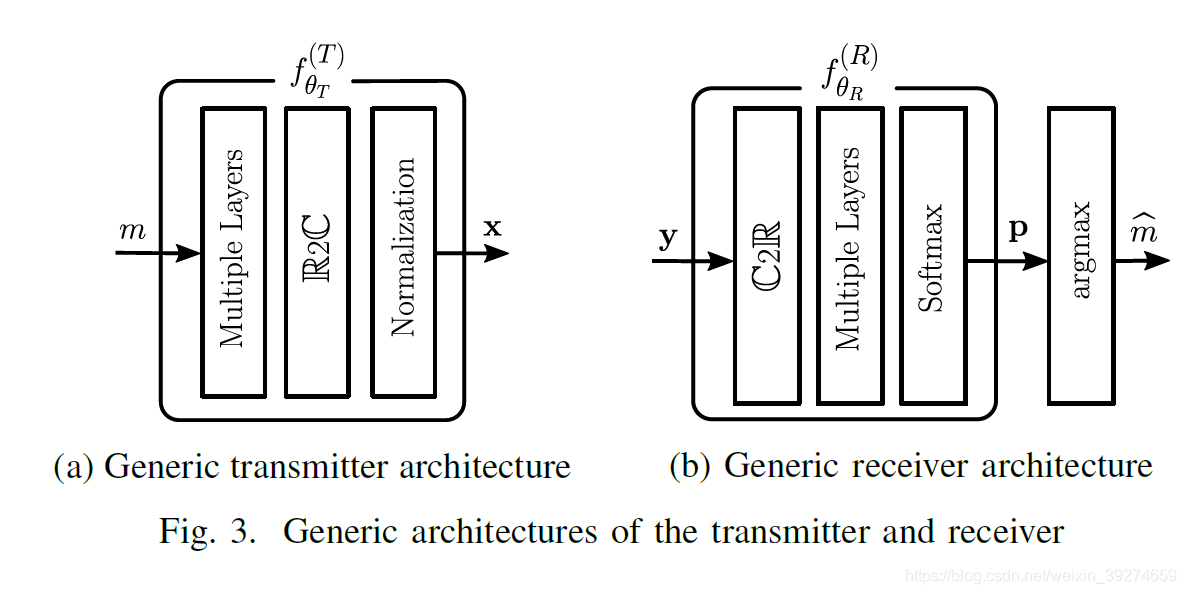
本文用两个独立的网络来实现发送端和接收端，这两个网络联合迭代优化，使得整体性能最佳。

发送端的神经网络（见Fig3 a）可表示为： $f_{\boldsymbol{\theta}_{T}}^{(T)} : \mathbb{M} \rightarrow \mathbb{C}^{N}$

• 发送端的normalization保证每个符号的平均功率为1
• 输入数据m采用one hot编码

接收端的神经网络（见Fig3 b）可表示为： $f_{\boldsymbol{\theta}_{R}}^{(R)} : \mathbb{C}^{N} \rightarrow\left\{\mathbf{p} \in \mathbb{R}_{+}^{M} | \sum_{i=1}^{M} p_{i}=1\right\}$

• 接收神经网络根据接收的数据y输出预测的条件概率p(m|y)。softmax输出的是软信息p(m|y)，通过argmax进行硬判。
• 更新参数θ_R，使交叉熵（cross entropy，CE）最小，（假设训练样本独立相同分布，S是训练集的大小） $\boldsymbol{\theta}_{R}^{*}=\underset{\boldsymbol{\theta}_{R}}{\arg \min } L\left(\boldsymbol{\theta}_{R}\right)$

$L\left(\boldsymbol{\theta}_{R}\right)=\frac{1}{S} \sum_{i=1}^{S} \underbrace{-\log \left(\left[f_{\boldsymbol{\theta}_{R}}^{(R)}\left(\mathbf{y}^{(i)}\right)\right]_{m^{(i)}}\right)}_{l^{(i)}}$

暂时遗留一个小问题（之后再做说明）：接收神经网络的输入y与发送神经网络输出x是什么关系？

训练流程

假定 $f_{\boldsymbol{\theta}_{T}}^{(T)}$ 和 $f_{\boldsymbol{\theta}_{R}}^{(R)}$可微，根据损失函数，使用梯度下降法来调整这两个网络的参数。在训练接收端时，发送端的参数固定；训练发送端时接收端的参数固定。步骤如下：

这个流程图表示得非常清楚了，下面进行简单的补充说明。

接收端训练

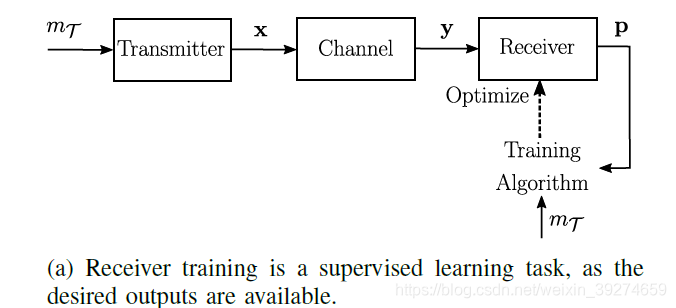
监督学习，损失函数为CE，B_R为batch size，这一阶段仅更新接收神经网络的参数

注意：在这一阶段，输入端神经网络的输出通过信道作为y，对比发送端训练时，神经网络的输出x需要先经过一个sample
policy再通过信道才得到y

发送端训练

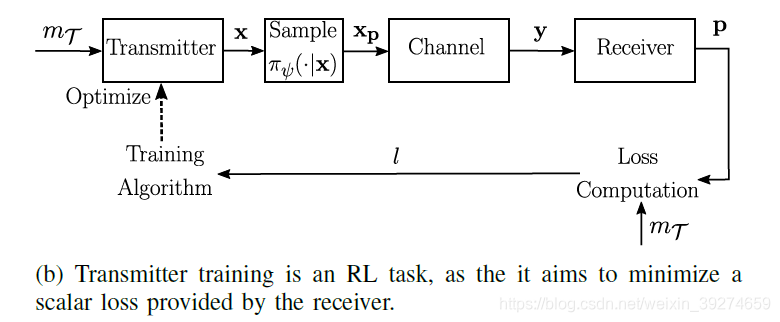
发送端训练的目标是生成最小化接收机提供的损失的信道符号。在这里神经网络输入空间M对应状态空间，输出空间 $\mathbb{C}^{N}$对应动作空间。

使用强化学习，损失函数充当奖励的功能，由接收端反馈给输入端，在这里使用高斯策略， $\mathbf{x}_{p}=\sqrt{1-\sigma_{\pi}^{2}} \mathbf{x}+\mathbf{w}$，其中 $\mathbf{w} \sim \mathcal{C} \mathcal{N}\left(\mathbf{0}, \sigma_{\pi}^{2} \mathbf{I}\right)$， $\sigma_{\pi} \in(0,1)$在这里是固定为0.02。sample policy相当于给神经网络的输出增加一个扰动，使它从原来的确定值变成满足高斯分布的输出。输入端的神经网络和sample policy共同组成发送端编码的策略函数。策略函数可表示为 $\begin{array}{l}{\pi\left(\mathbf{x}_{p} | f_{\boldsymbol{\theta}_{T}}^{(T)}(m)\right)=} \\ {\frac{1}{\left(\pi \sigma_{\pi}^{2}\right)^{N}} \exp \left(-\frac{\left\|\mathbf{x}_{p}-\sqrt{1-\sigma_{\pi}^{2}} f_{\boldsymbol{\theta}_{T}}^{(T)}(m)\right\|_{2}^{2}}{\sigma_{\pi}^{2}}\right)}\end{array}$
loss gradient可表示为 $\begin{array}{l}{\nabla_{\boldsymbol{\theta}_{T}, \boldsymbol{\psi}} \tilde{J}\left(\mathbf{m}_{\mathcal{T}}, \mathbf{l}, \mathbf{X}_{p}\right)} \\ {\quad=\frac{1}{B_{T}} \sum_{i=1}^{B_{T}} l^{(i)} \nabla_{\boldsymbol{\theta}_{T}, \boldsymbol{\psi}} \log \left(\pi_{\boldsymbol{\psi}}\left(\mathbf{x}_{p}^{(i)} | f_{\boldsymbol{\theta}_{T}}^{(T)}\left(m_{\mathcal{T}}^{(i)}\right)\right)\right)}\end{array}$
将 $\begin{array}{l}{\nabla_{\boldsymbol{\theta}_{T}} \log \left(\pi\left(\mathbf{x}_{p} | m\right)\right)} \\ {\quad=\frac{2 \sqrt{1-\sigma_{\pi}^{2}}}{\sigma_{\pi}^{2}}\left(\nabla_{\boldsymbol{\theta}_{T}} f_{\boldsymbol{\theta}_{T}}^{(T)}(m)\right)^{\top}\left(\mathbf{x}_{p}-\sqrt{1-\sigma_{\pi}^{2}} f_{\boldsymbol{\theta}_{T}}^{(T)}(m)\right)}\end{array}$

代入上式即可更新参数。

现在可以回答之前遗留的小问题了：在训练发送端时，y=hx_p；在训练接收端时，y=hx

关于接收端训练的一个疑问：为什么训练接收端时不经过sample policy，放松神经网络的输出？这样训练出来的接收端参数并不匹配实际使用的发送端学习到的编码策略

仿真结果

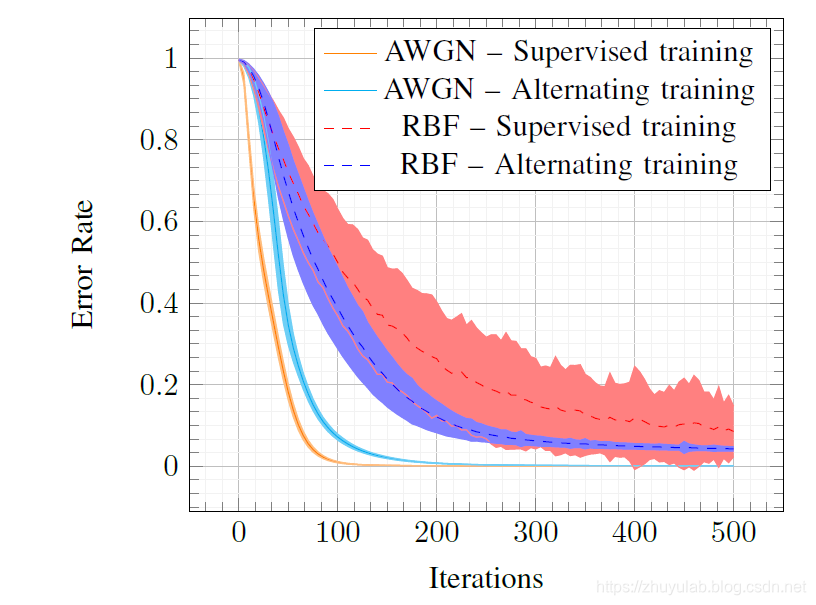
• 在高斯信道下，迭代的方法比监督学习算法收敛慢，但能得到几乎一样的性能
• 在瑞利信道下，迭代的方法比监督学习算法收敛快，且性能更好。对此作者的解释是：监督学习算法中梯度直接受到信道响应的影响，该通道响应是随机的，因此导致高梯度方差。然而，利用交替方法，提供给发射机的损失受随机信道响应的影响较小，不会出现高梯度方差的问题。

我的理解

• 知道channel function肯定是有好处的，发送接收分开训练在避开channel function时带来的问题是，在训练发送端时需要的损失函数必须通过一个可靠的信道反馈给输入端（就好比现实中，好处总不能你一个人全占了，此消彼长嘛）。而在实际系统中，上行链路和下行链路是满足共轭关系的，这就表明这个训练方法其实只适合用在可靠信道上。这与作者的结论——由于不需要知道信道模型，此方法可以用在任何未知信道并不符合。
• 看起来实现“避免使用信道模型”的是策略目标函数的形式，其实本质上是改变了损失函数作用于发送端的形式：原来的方法通过反向传播作用，这个方法将损失通过上行链路反馈回发送端去更新参数，这样发送端就有了一个与loss有关的优化方向。就算不使用所谓的策略目标函数，使用其他的目标函数也是可以的。