[新坑]以后做的简单数论题就总结在这了

emm，数学是我心中永远的痛。

逆元

1. P3811 【模板】乘法逆元

P3811 【模板】乘法逆元

给定 $n$与 $mod$，求出 $1\sim n$所有整数在模 $mod$下的乘法逆元。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=3e6+5;
ll inv[maxn],mod,n;
int main()
{
	cin>>n>>mod;
	inv[0]=inv[1]=1;
	for(int i=2;i<=n;i++)
		inv[i]=(mod-mod/i)*inv[mod%i]%mod;
	for(int i=1;i<=n;i++)
		cout<<inv[i]<<'\n';
	return 0;
}

整除分块

1. CF1263C Everyone is a Winner!
2. UVA1363 约瑟夫的数论问题Joseph’s Problem

CF1263C Everyone is a Winner!

题意

给定 $n$，求对任意正整数 $k$， $\llcorner\dfrac{n}{k} \lrcorner$存在多少种不同的数值并输出。

做法

整除分块模板题，开一个栈记录答案即可。

代码

之前写过就不在这里贴了

UVA1363 约瑟夫的数论问题 Joseph’s Problem

题意

给定 $n$与 $k$，计算 $\sum\limits_{i=1}^n k\% i$

做法

$\sum\limits_{i=1}^n k\% i=\sum\limits_{i=1}^n \left( k-\llcorner\dfrac{k}{i} \lrcorner\times i\right)=k\times n -\sum\limits_{i=1}^n\llcorner\dfrac{k}{i} \lrcorner\times i$
注意 $n$与 $k$的大小。
当 $i\geq k$时， $\llcorner\dfrac{k}{i} \lrcorner=0$，不会对答案造成影响。
所以 $n\ge k$的部分不必计算，特判跳出，防止TLE。
当 $k\ge n$时，又要取 $min(l/(k/l),n)$，防止多减。
对于每一块，都可以看做首项为 $l$，公差为 $1$的等差数列。

代码

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int main()
{
	ll n,k;
	while(~scanf("%lld%lld",&n,&k))
	{
		ll ans=k*n;
		for(ll l=1,r=1;l<=k;l=r+1)
		{
			if(k/l==0||l>n)
				break;
			r=min(k/(k/l),n);//防止多减
			ll x=r-l+1;//项数
			ans-=(k/l)*(x*l+x*(x-1)/2);
//			printf("l=%lld,r=%lld,del=%lld,x=%lld,ans=%lld\n",l,r,n/l,x,ans);
		}
		printf("%lld\n",ans);
	}
	return 0;
}

组合数学

斐波那契

1. [P3938 斐波那契](https://www.luogu.com.cn/problem/P3938

P3938 斐波那契

题意请看原题。

做法

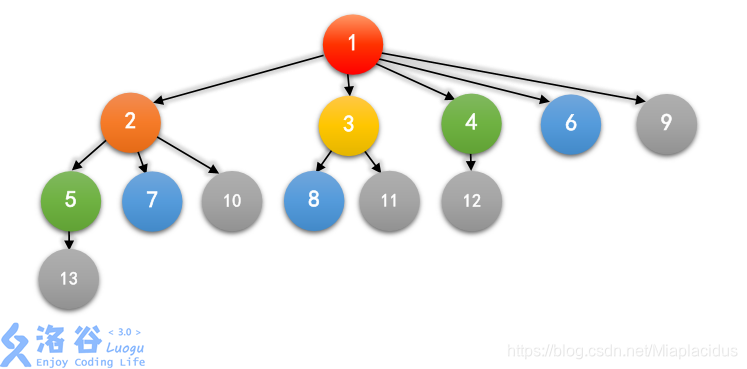
二分，数论，LCA概念
蒟蒻只能找规律，可以发现每代新增 $f[i-2]$
则第 $i$代时兔子总数 $f[i]=f[i-1]+f[i-2]$，同时第 $i$代出生的第 $j$只兔子的编号为 $f[i-1]+j$。
观察规律可发现， $j$即为父节点编号。
所以当我们找一只兔子的爸爸时，可以先在斐波那契数组上二分出这只兔子所处第几代， $兔子爸爸编号=兔子编号-上一代总共兔子数$，上一代兔子数为 $f[i-1]$， $i$即为当前兔子所处世代。

代码

#include<bits/stdc++.h>
using namespace std;
#define int long long
int fibo[62]={1,1};
signed main()
{
	for(int i=2;i<62;i++)
		fibo[i]=fibo[i-1]+fibo[i-2];
	int t;
	cin>>t;
	while(t--)
	{
		int a,b;
		cin>>a>>b;
		while(a!=b)
		{
			if(a<b)
				swap(a,b);
			int gene=lower_bound(fibo,fibo+62,a)-fibo;//找到第一个不比a小的,记录编号,编号x即a为第x代
			a-=fibo[gene-1];//减去上一代总数,此时a为父节点编号
		}
		cout<<a<<endl;
	}
	return 0;
}

第二类斯特林公式

定义：将n个不同物体划分到m个非空无差别集合的方案数,记为 $S(n,m)$。
递推公式： $dp[n][m] = dp[n-1][m-1]+dp[n-1][m] * m$

1. P1655 小朋友的球

P1655 小朋友的球

题意

裸题

AC的代码

while True:
    try:#本题求出斯特林数s[n][m]
        n,m=list(map(int,input().split()))
        s=[[0 for col in range(105)] for row in range(105)]
        s[0][1]=1
        for i in range(1,n+1):
            for j in range(1,i+1):
                s[i][j]=s[i-1][j-1]+s[i-1][j]*j
        if(m>n):
            print(0)
        else:
            print(s[n][m])
    except EOFError:
        break