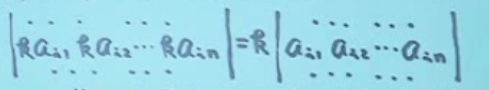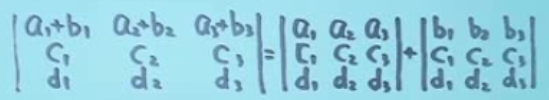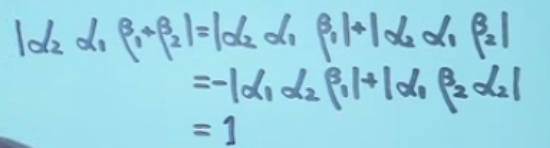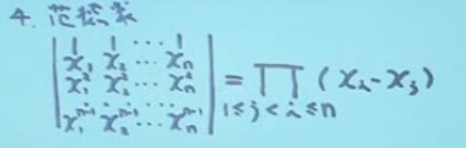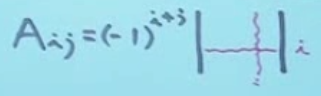【线性代数专栏】
A 行列式
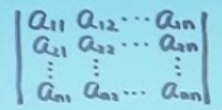
行列式:不同行不同列元素乘积的代数和。(共
n!项)
A.a 行列式的计算
(1)二阶行列式:
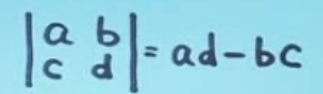
(2)三阶行列式:

主对角线减副对角线:
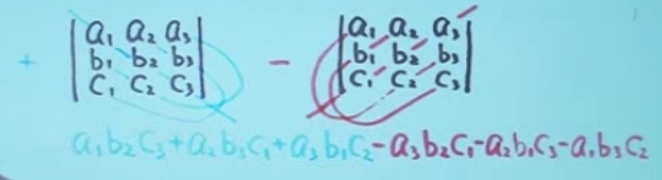
(3)多阶行列式:
行列式按行展开(降阶)公式:
∣A∣=ai1Ai1+ai2Ai2+...+ainAin
其中: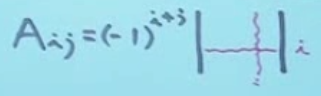
为代数余子式子(注意符号)。
例子: 但是有时候这样计算量太大,所以要先恒等变形。
但是有时候这样计算量太大,所以要先恒等变形。
(4)逆序、逆序数
- 排列:由
1,2,...,n组成的有序数组称为一个
n阶排列,通常用
j1,j2,...jn表示
n阶排列。
例如:
2413——4阶排列
13542——5阶排列
- 逆序:一个排列中,如果一个大的数排在小的数之前,就称这两个数构成一个逆序。
- 逆序数:一个排列的总序总数称为这个排列的逆序数。用
τ(j1,j2,...,jn)表示排列
j1,j2,...,jn的逆序数。
如果一个排列的逆序数是偶数,则称这个排列是偶排列,否则称为奇排列。
τ(2431)=1+2+1=4(2比1大,4比3和1大,3比1大)
τ(31532)=2+0+2+1=5(3比1和2大,1,5比4和2大,4比2大)
行列式的计算:
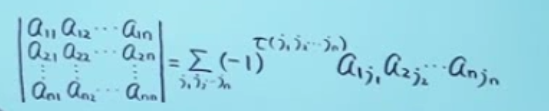 j有n!种排列,故得到n!个项相加减。
j有n!种排列,故得到n!个项相加减。
例子:

例子:

x3一定不含
a14,
a41:由于相乘的
a是不同行不同列的,
a14,
a41与其他两行不同列的元素组成
x3时,剩余一行能取的元素为
x.
A.b 行列式的性质
-
1、经转置行列式的值不变
∣AT∣=∣A∣
-
2、两行互换行列式的值变号。
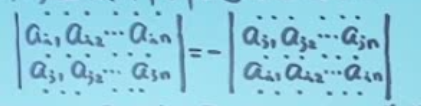 特别地,两行相同行列式的值为0。
特别地,两行相同行列式的值为0。
-
3、某行如果有公因数
k,可把
k提出行列式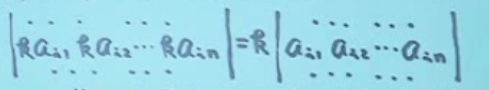
特别地,某行元素全为0,行列式的值为0。两行成比例,行列式的值为0。
-
4、如果某行元素是两个数之和,可把行列式拆成两个行列式之和
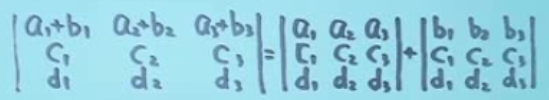
-
5、某行的
k倍加至另一行行列式值不变。

例题1:
α1,α2,β1,β2都是三维列向量,若
∣α1α2β1∣=5,∣α1β2α2∣=6,∣α2α1β1+β2∣=?
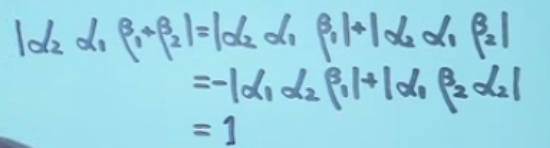
例题2:
证:
例子3:
A.c重要公式


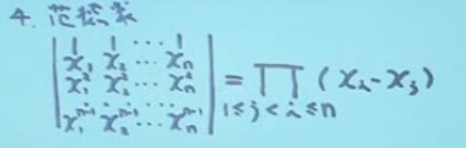
xi−xj
B 克拉默法则
用于n个方程n个未知数。



例题:

D用为范德蒙行列式
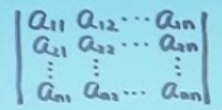
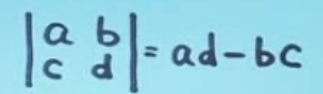

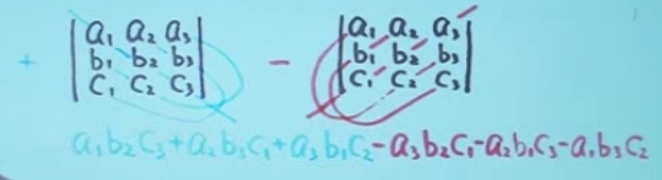
 但是有时候这样计算量太大,所以要先恒等变形。
但是有时候这样计算量太大,所以要先恒等变形。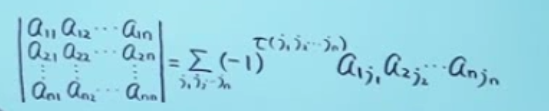 。
。

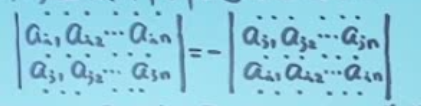 特别地,两行相同行列式的值为0。
特别地,两行相同行列式的值为0。