【RS】因子分解机FM

2020.2.22.从本篇开始，所有文章使用markdown编辑
为什么使用FM？
机器学习的通常模式为学习输入到输出的变换，比如最常见的线性回归模型，对于特征向量
\(X=\left(x_{1}, x_{2}, \ldots, x_{n}\right)^{T}\)
我们有目标预估函数
\(\begin{aligned} \hat{y}(x) &=w_{0}+w_{1} x_{1}+w_{2} x_{2}+\ldots w_{n} x_{n} \\ &=w_{0}+\sum_{i=1}^{n} w_{n} x_{n} \end{aligned}\)
线性回归是最简单的线性模型，是基于各个特征独立同分布的假设，只能捕捉到一阶线性关系。
事实上，各个特征并不是相互对立的，有些特征是相互影响的，此时就有了二阶特征表达式，考虑了两个特征变量之间的交互影响。
\(\widehat{y}(x)=w_{0}+\sum_{i=1}^{n} w_{n} x_{n}+\sum_{i=1}^{n} \sum_{j=i+1}^{n} w_{i j} x_{i} x_{j}\)
这里每俩个特征就有一个参数\(W_{1 j}\)需要学习。但是这里有一个问题，对于二项式回归来说，如果有n个特征，那么就要学习到俩俩之间的关系，那么就有n(n-1)/2个参数需要学习，参数数量特别多。
既然每一个参数\(W_{1 j}\)都是二阶特征，我们可以把对于\(W_{1 j}\)的估计，转换成为矩阵分解MF问题：

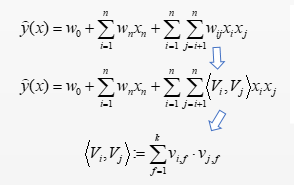
如果直接计算，如图所示，复杂度为\(O\left(k^{*} n^{2}\right)\)，n是特征个数，K是特征的embedding size