这篇笔记基于上一篇《关于GAN的一些笔记》。
1 GAN的缺陷
由于 $P_G$ 和 $P_{data}$ 它们实际上是 high-dim space 中的 low-dim manifold,因此 $P_G$ 和 $P_{data}$ 之间几乎是没有重叠的
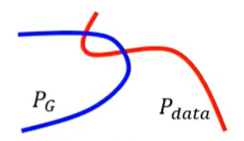
正如我们之前说的,如果两个分布 $P,Q$ 完全没有重叠,那么 JS divergence 是一个常数 $\log(2)$。
由于最优的 generator 是
![]()
我们在普通的 GAN 中,最小化的是 $P_{data}$ 和 $P_G$ 之间的 JS divergence,那么由于 $P_G$ 和 $P_{data}$ 之间几乎是没有重叠的,所以往往会导致 $P_G$ 和 $P_{data}$ 之间的 JS divergence 接近于 $\log(2)$。
由于无法判别到底那种情况下两个分布更加接近,这就意味着有时候普通的 GAN 很难训练,甚至没法训练。
而如果我们采用实际代码实现中的 NSGAN,即把 generator 的 loss 改成
![]()
首先请注意,我们训练 generator 时,discriminator 是固定的,不妨记作 $D^{*}$,而 $D^{*} = P_{data}(x) / (P_{data}(x) + P_G(x))$,这里的 $P_G$ 是还未更新的 generator $G$ 所对应的 distribution。
由于我们已知(详细的推导可以参见《关于GAN的一些笔记》)
![]()
类似的我们也可以把 KL divergence 写成
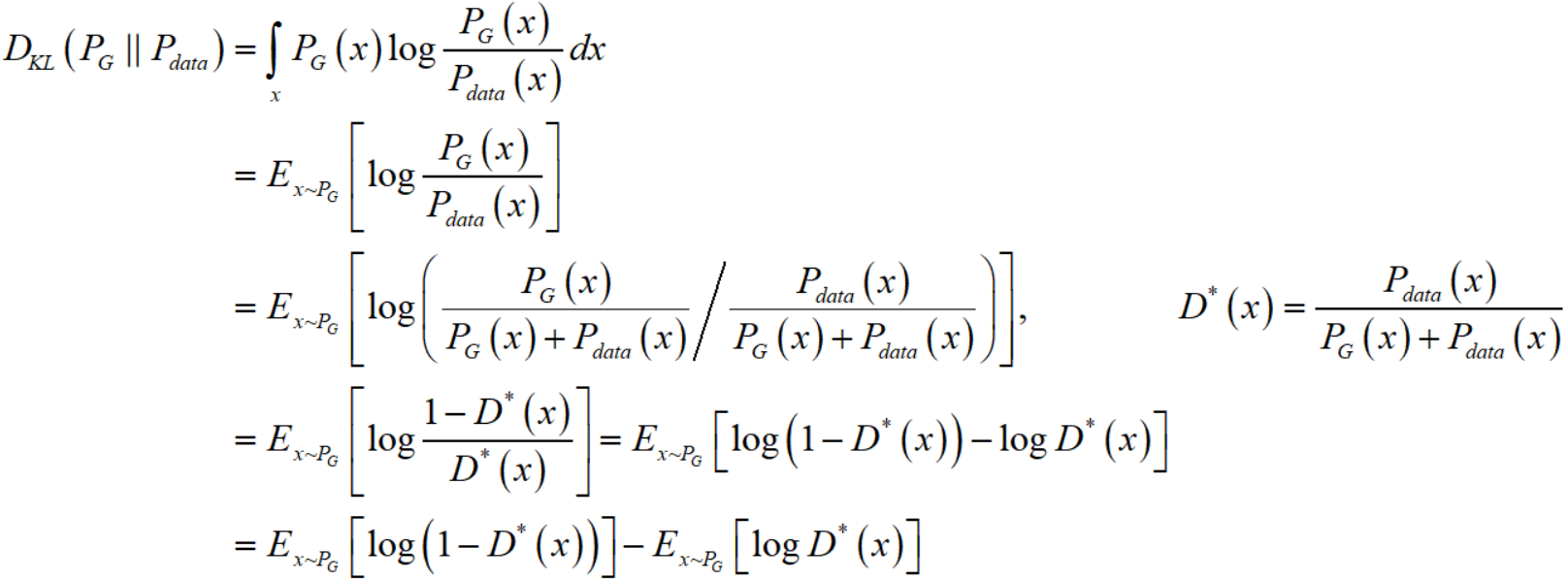
所以
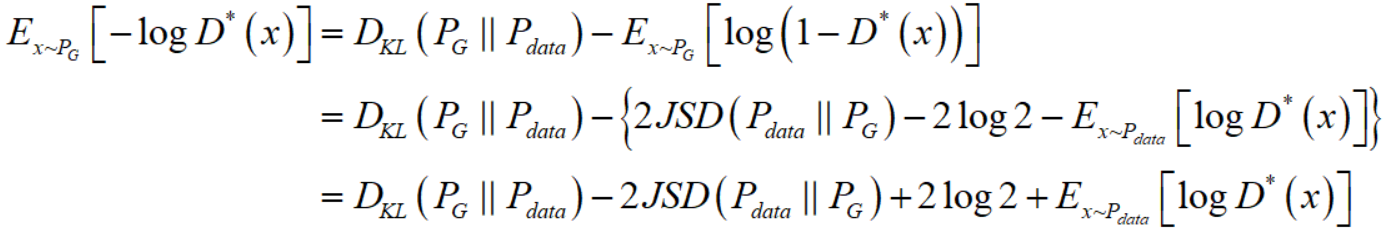
注意到对于后两项,一项是常数项,一项是更改 $G$ 无法影响的(当你训练 $G$ 时,$D$ 是固定的,同时 $P_{data}$ 显然也是不会变的)。所以,你如果把 generator 的 loss 改成了 $V = E_{x \sim P_G}[-\log D(x)]$,那么你就相当于在寻找最优的 generator
![]()
这显然在理论上是站不住脚的,一边想使得两个分布的 KL divergence 尽量小,一边又想要使得两个分布的 JS divergence 尽量大,这是矛盾的。这在数值上则会导致梯度不稳定,这就是后面那个 JS divergence 所带来的问题。
而且另外一个问题是 KL divergence 是非对称的,会带来以下问题:
首先写出 $D_{KL}(P_G \parallel P_{data}) = \int_{x} P_G(x)\log \frac{P_G(x)}{P_{data}(x)}dx$,我们分两种情况考虑 generator $G$ 会犯的错误:
① 对于某处的 $x$,$P_G(x)$ 是高概率(接近 $1$)而 $P_{data}(x)$ 是低概率(接近 $0$),那么此时 $P_G(x)\log \frac{P_G(x)}{P_{data}(x)}$ 接近于正无穷,对于 $D_{KL}(P_G \parallel P_{data})$ 产生了巨大的贡献。
② 对于某处的 $x$,$P_G(x)$ 是低概率(接近 $0$)而 $P_{data}(x)$ 是高概率(接近 $1$),那么此时 $P_G(x)\log \frac{P_G(x)}{P_{data}(x)}$ 接近于 $0$,对于 $D_{KL}(P_G \parallel P_{data})$ 产生了微乎其微的贡献。
这就导致了,对于错误①(generator 生成了不符合 $P_{data}$ 的错误图片)惩罚巨大,而对于错误② (generator 没有尽可能生成符合 $P_{data}$ 的正确图片)惩罚很小。这就是的 generator $G$ 会多生成一些重复的但是符合 $P_{data}$ 的正确图片,而不愿意去生成多样性的样本,因为那样就很容易产生错误①,会受到巨大的惩罚。这种现象就是大家常说的 collapse mode。这应该就是《关于GAN的一些笔记》中生成结果中有大量的“$1$”的原因。
2 WGAN
之前在《关于GAN的一些笔记》中写到了 Wasserstein distance 相较于 JS/KL divergence 的优越性。就算 $P_G, P_{data}$ 之间没有重叠也可以衡量两个分布的距离。
当然,$W(P,Q) = \inf\limits_{\gamma \in \Pi(P_{data},P_G)} E_{(x,y) \sim \gamma}[\left \| x-y \right \|]$ 这种形式没法直接变换得到objective function。但是可以用一个定理将其变换成如下形式
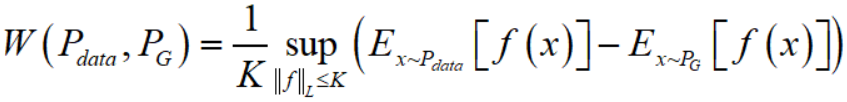
这里需要用到的一个知识是 Lipschitz 连续,它对一个函数 $f$ 施加一个限制,要求存在一个常数 $K$ 使得 $f$ 的定义域内任意的两个元素 $x_1, x_2$ 都满足
![]()
形象一点的描述就是迫使函数不能过分陡峭,此时成函数 $f$ 的 Lipschitz 常数为 $K$。
所以,变换后的 Wasserstein distance 的意思就是在要求函数 $f$ 的 Lipschitz 常数 $\left \| f \right \|_{L}$ 不超过 $K$ 的条件下,对所有可能满足条件的 $f$ 取到 $E_{x \sim P_{data}}[f(x)] - E_{x \sim P_G}[f(x)]$ 的上界,然后再除以 $K$。假设我们有一组参数 $w$ 来