第四章 二元关系和函数 4.2 关系运算

4.2 关系运算

1.关系的集合运算
上一节提到了，关系本身也是一种集合，所以其可以进行集合的基本运算。

2.关系的逆运算

例：

解：


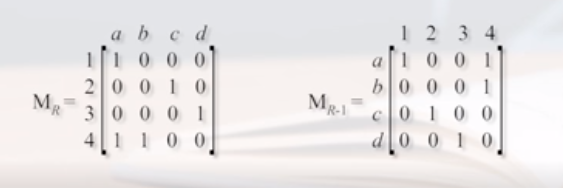
可见这两个矩阵互为转置矩阵。
由上述例题我们可以总结出以下几个性质：

对于逆关系我们还有如下性质：

还记得我们之前说的命题演算法吗？这里我们用命题演算法来证明第二条性质：

3.关系的合成运算

写一大堆也不好理解，简单说就是：
先R后S（将R最后一项与S的第一项进行合并）

例：

关系的合成运算是符合结合律的，下面我们还用命题演算来证明：

关系运算的分配律比较特殊，请看：

由此可见：合成运算对于并运算是可分配的，但对交运算分配以后得到的是不等式（一个包含关系）

这是因为，我们把他拆开最前面是存在量词 $\exists$，之前我们也提到了，存在量词把并运算 $\wedge$展开后得到的是一个包含关系。

说严谨一点就要用到我们之前讲到的量词分配律。
如下：

合成运算有如下性质：

既然是合成运算那么就不止两个关系来合成：

以下是其一些性质：

例：

由此可见：

下边我们来用关系矩阵的乘法来求合成运算的结果
例：

因为R的列数不等于S的行数，所以这里我们将 $M_R$矩阵进行了扩展。
接下来我们将他们的关系矩阵进行乘法操作：

注意：这里的行序号是1,2,3。列序号是1,2,3,5。

综上可知：
S $\circ$ R = {(1,5) , (2,5), (3,2)}

练习1：


正确答案： A

解析：
对于 $S^{-1}$，我们只需把（x,y）变成（y,x）即可。不需要把里面的关系再换位置，否则相当于没转换。

练习2：
设A = {a,b,c,d} ， R为A上的关系，R={(a,a),(a,b),(b,d),(c,d)}, $R^2$为()？