Chango的数学可视化（二）向量场：梯度，散度，拉普拉斯

起因：

在没有看梁昌洪老师的公开课之前，对向量场知识一无所知，碰到泊松融合，泊松重建的文章时非常痛苦。现在将知识慢慢补起来，并用程序可视化，一来巩固知识，二来了解离散化形式和其实际中遇到的问题。

目的：

从Poisson Surface Reconstruction一文得到启发。

先模拟一个包含目标点云的数量场，使得模型点云的数量值为1，其他为0。

通过对此数量场进行一次梯度算子 $\bigtriangledown$ ，得到一向量场，也就是其表面内法线估计；

再对此向量场进行一次 $\bigtriangledown$ ，得一数量场，也就是表面指示数量场，即数值为1的点就是表面。

当然其中对比实际和论文有很多简化和差异，不再赘述。

本文就是一个3D版laplace边缘检测，但出发点是矢量场的内容。

步骤：

梯度指向最大变化方向

散度表示源状态

1.建立模型点云和数量场

简单认为模型就是一个完美球。而我们的点云也都是网格对齐的。

模型点值为1，其他为0。

2.使用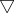 $\bigtriangledown$ 得矢量场。

对于离散情况得3D梯度算子，我直接从2D形式推广，也就是

$(\frac{x2-x1}{2},\frac{y2-y1}{2},\frac{z2-z1}{2})$

至于怎么来得，2D形式推导可参考我之前写的：

Chango的数学Shader世界（十）流体模拟-有限微分形式

此时，只有模型表面点梯度才不为0向量，为模型表面内法线方向。

在离散情况下,由于我们离散梯度计算的原因，表面“接壤”的黑色层和白色层两个点梯度都不会为0.

3.再使用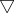 $\bigtriangledown$ 得laplace数量场。

为什么我不从一开始的数量场1步推导laplace算子 $\Delta$ 到laplace数量场？

因为一来可以学会梯度场到数量场的转换，二来在泊松融合等实际应用中，都是将背景图的梯度场与ROI的梯度场相加，再 $\bigtriangledown$ 的，否则仅用ROI的laplace结果然后加上去边缘必然无法融合。（3D模型泊松融合也是一样的道理）。

所以分两步走是必然的。

那么怎样离散的laplace怎么得到呢？这里有点绕。

我们知道连续函数有 $\Delta=\frac{\partial ^{2}}{\partial x^{2}}+\frac{\partial ^{2}}{\partial y^{2}}+\frac{\partial ^{2}}{\partial z^{2}}$ ，laplace由三部分相加组成。

现在，尝试取梯度场的x分量组成数量场，此数量场是 $\frac{\partial f}{\partial x}$ ,因为我们的梯度场是 $(\frac{\partial f}{\partial x},\frac{\partial f}{\partial y},\frac{\partial f}{\partial z})$ 。

再求此数量场的梯度，则得梯度场 $\bigtriangledown\frac{\partial f}{\partial x} = (\frac{\partial^{2} f}{\partial x^{2}},\frac{\partial f}{\partial x\partial y},\frac{\partial f}{\partial x\partial z})$ ,那我们可以发现，所需的 $\frac{\partial^{2} f}{\partial x^{2}}$ 是其第一个分量。

我们再来捋一捋，之前算离散梯度是 $(\frac{x2-x1}{2},\frac{y2-y1}{2},\frac{z2-z1}{2})$ == $(\frac{\partial f}{\partial x},\frac{\partial f}{\partial y},\frac{\partial f}{\partial z})$ 。

所以，现在有了梯度场，要求 $\frac{\partial^{2} f}{\partial x^{2}}$ ，则只要关心x方向vx1,vx2两个向量的x值，就是对应离散梯度的x1,x2。

所以计算得(vx2.x-vx1.x)/2。

$\frac{\partial^{2} f}{\partial y^{2}}$ , $\frac{\partial^{2} f}{\partial z^{2}}$ 同理，最后相加即可。