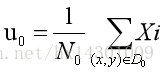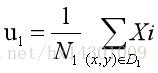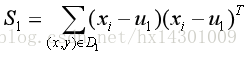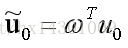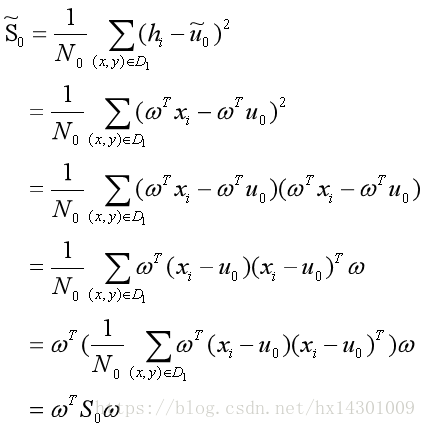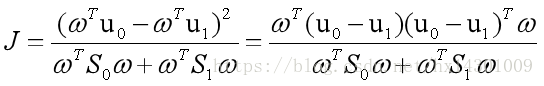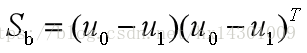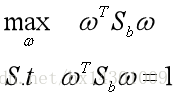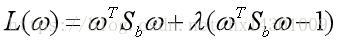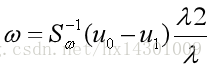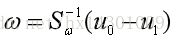LDA线性判别分析（Linear Discriminant Analysis）最早由Fisher提出，也叫“Fisher判别分析”。
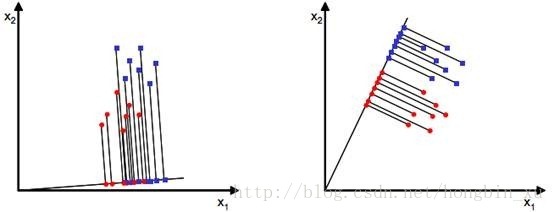
线性判别分析的思想：给定样本数据集，设法将样本投影到某一条直线上，使得同类样本的投影点尽可能接近，异类样本的投影点尽可能远离；在对新的点进行分类预测时，将其投影到这条直线上，根据投影点的位置来判断样本的类别。
当x是二维时，我们就要寻找一个方向为ω的直线来使得这些样本点的投影分离。
如下图所示：
二分类情况：
先只考虑二分类情况，给出数据集
,
.
设有No个样本的label为Yi=0，类别为Do；N1个样本的label为Yi=1，类别为D1.
则：D0与D1的均值向量为：
再给出一组新的度量：散度值（scatter）
这东西看上去很熟悉吧，不就是方差少除了样本数量吗？因为这里只需要定量表示样本集合的分散程度，对常数系数不敏感，所以这样就足够了。
给出一组参数ω，假设值为：
，后面简写为
。
在线性回归中，我们的目标是使得这个假设值等于样本的label Yi；而在线性判别分析中，假设值hi实际是样本hi在ω方向上的投影的长度；以二维的情况考虑，就是样本Xi对应的点(x1,x2)到直线ω的投影点到原点的长度。我们的目标是通过区分这个“长度hi”；
接着，根据ω可以求出投影后的样本均值
与
：
，
同理可得：
投影后的散度矩阵：
同理：
希望同类样例的投影尽可能接近，即散度矩阵尽可能小，即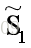
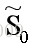
异类样例的投影点尽可能远，即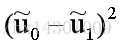
同时考虑上面两个条件，可以给出目标函数
令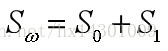
前者为类内散度矩阵， 后者为类间散度矩阵
则： 
这就是LDA欲最大化的目标函数，即Sω与Sb的“广义瑞利商”（generalized Rayleigh Quotient）
OK，接下来的任务就是通过 J 来确定最优的ω
由于①的分子与分母都是关于ω的二次项，因此J的大小不随ω的大小变化，上下抵消后，结果只与其方向有关。
不失一般性，令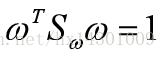
由拉格朗日乘子法得：(即条件极值)
求导并令导数为0的解得：
-----------------②
又因为
， 且
恒为一个常数，
可以看出
的方向恒为
因此不妨设
，------------------------③
由②与③得：
因为最后的结果只与ω的方向有关，因此
可以舍去。
得：
这就是最终结果，前面已经推导出了
、
、
，代入即可。我们只要有散度矩阵和均值即可求出最优的ω
这里还有一点，考虑到数值解的稳定性，在实践中通常是对
后面的多分类线性判别，这个涉及更多矩阵东西了，没看懂，等以后懂了再记下来。
