机器学习——线性判别分析

什么是线性判别分析

引自周志华老师的《机器学习》

线性判别分析是一种经典的线性学习方法，给定训练样例集，设法将样例投影到一条直线上，使得同类样例的投影点尽可能的近，异类样例的投影点尽可能原，在对新样本进行分类时，将其投影到同样的这条直线上，在根据投影点的位置来确定新样本的类别

一个直观的例子：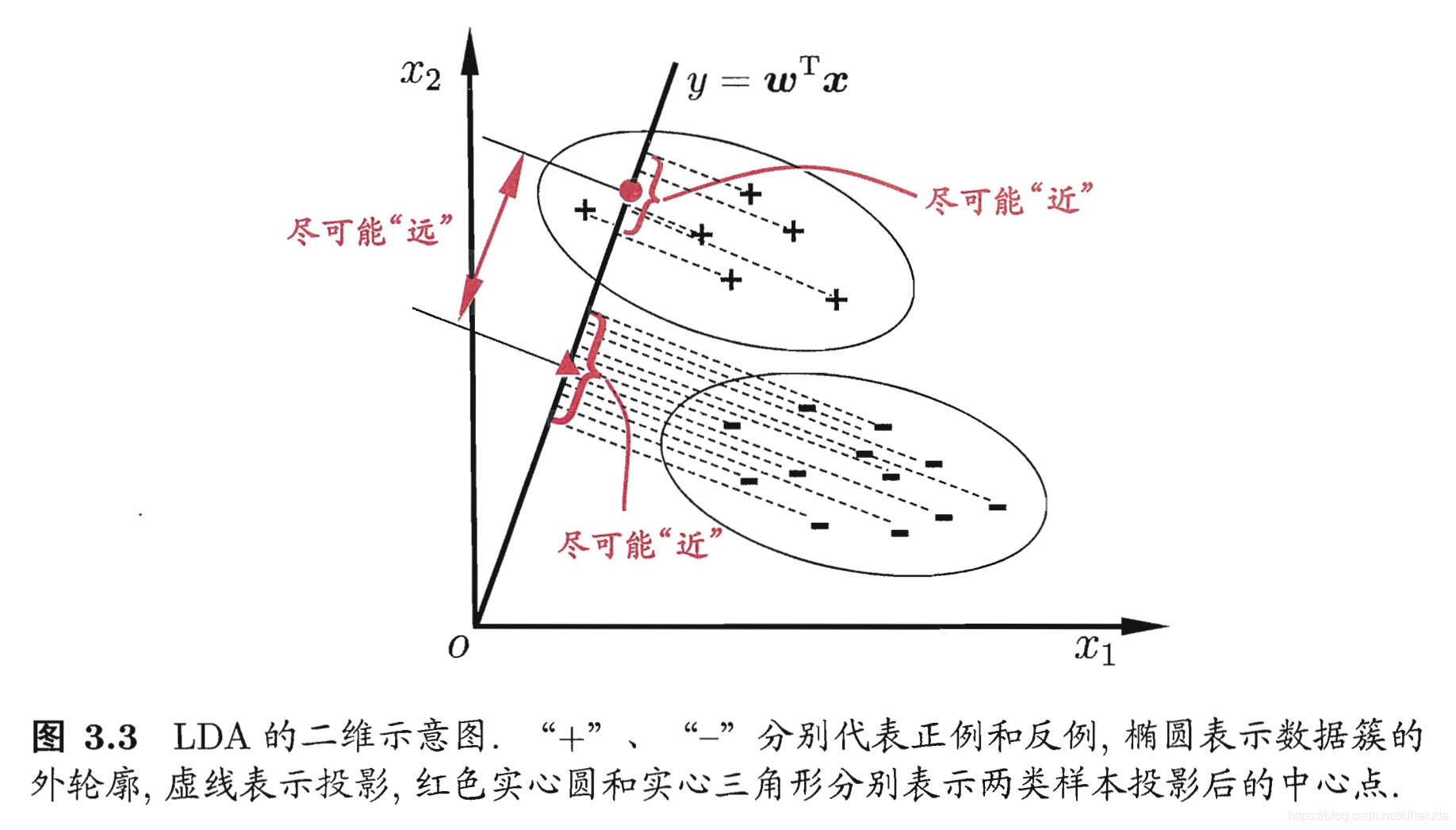

线性判别分析的作用

1、分类
2、降维，其将高维空间的点映射到一条直线上，用一个实数来表示高维空间的点

基本思想

线性判别分析具有两个关键点

• 1、投影后，不同类别的点尽可能远离
• 2、投影后，相同类别的点尽可能靠近

对于关键点1，我们可以使用投影后，不同类别的中心点之间的距离来衡量，中心点距离越远，类别之间的区分度越高

对于关键点2，我们可以使用方差来衡量投影后同类别点之间的散乱程度（方差的统计意义便是衡量点与点之间的散乱程度），方差越小，投影后同类别的数据之间越靠近

如何将点投影到直线上

周志华老师的《机器学习》一书并没有明显说明如何将点投影到直线上，那么我们如何用式子去刻画点投影到直线这个动作呢？即如何寻找到一个式子，使其几何意义表示将点投影到某个直线上

我们来看看维基百科对于线性回归的定义 我是链接：

线性判别分析 (LDA)是对费舍尔的线性鉴别方法的归纳，这种方法使用统计学，模式识别和机器学习方法，试图找到两类物体或事件的特征的一个线性组合，以能够特征化或区分它们

关键点在于LDA试图通过特征的线性组合来特征化或区分它们，若特征为（ $x_{1}$, $x_{2}$,…, $x_{d}$），那么LDA的输出应该是

y= $w_1x_1$+ $w_2x_2$+…+ $w_nx_d$ （式1.0）

问题是，这个式子的几何意义是什么？
令 $w$=( $w_1$, $w_2$,…, $w_d$)，x=（ $x_1$, $x_2$,…, $x_d$），则式1.0可重写为

y= $w^Tx$ (式1.1)

式1.1可看成是向量 $w$与向量 $x$的点乘，我们知道向量点乘可以写成：
$w^T*x$=| $w$|| $x$|cos $\theta$，其几何意义为向量 $x$在向量 $w$方向的投影长度的| $w$|倍，那么投影的直线便确定了，即向量 $w$所在方向的直线，但是线性判别分析是将训练集样例投影到直线上，但是式1.1是投影后在乘以| $w$|倍，是不是与线性判别分析的思想有出入呢？其实没有，因为对于所有的样例，式1.1都对其在 $w$方向的投影放大了| $w$|倍，不会改变投影后样例之间的相对位置，而线性判别的关键点只关心投影后点与点之间的相对位置关系，式1.1并不会破坏这个关系

二分类线性判别分析

接下来的任务就是如何使用式1.1去刻画上述两个关键点，即利用式1.1推出一个式子，其几何意义为这两个关键点，假设我们现有一个问题——判断一个工厂生产的零件是不是好零件，一个零件只有好和坏之分，因此这是一个二分类问题，设一个零件具有d个特征，我们用这d个特征去描述这些零件，现假设我们有一批样本数据，其中，好零件的样本为（ $x_{11}$, $x_{12}$,…, $x_{1n}$）,（ $x_{21}$, $x_{22}$,…, $x_{2d}$）,…,（ $x_{n1}$, $x_{n2}$,…, $x_{nd}$）,坏零件的样本为（ $x_{11}^,$, $x_{12}^,$,…, $x_{1n}^,$）,（ $x_{21}^,$, $x_{22}^,$,…, $x_{2n}^,$）,…,（ $x_{n1}^,$, $x_{n2}^,$,…, $x_{nd}^,$）

如何刻画类别的中心点之间的距离

即如何刻画投影后的中心点（均值），我们先求出投影前的均值向量
好零件的均值向量 $\overline{x}$为

（ $\frac{\sum_{i=1}^nx_{i1}}{n}$， $\frac{\sum_{i=1}^nx_{i2}}{n}$，…， $\frac{\sum_{i=1}^nx_{id}}{n}$）

投影后，各样本的值为
$\sum_{i=1}^nw_ix_{1i}$， $\sum_{i=1}^nw_ix_{2i}$，…， $\sum_{i=1}^nw_dx_{di}$

投影后，样本的均值为

$\frac{ \sum_{i=1}^nw_ix_{1i}+\sum_{i=1}^nw_ix_{2i}+...+\sum_{i=1}^nw_ix_{di}}{n}$ （式1.2）

（式1.2）可变为：

$\frac{w_1\sum_{i=1}^nx_{i1}}{n}$+ $\frac{w_2\sum_{i=1}^nx_{i2}}{n}$+…+ $\frac{w_d\sum_{i=1}^nx_{id}}{n}$（式1.3）

（式1.3）可变为：

$（w_1，w_2，...，w_d）^T$*（ $\frac{\sum_{i=1}^nx_{i1}}{n}$， $\frac{\sum_{i=1}^nx_{i2}}{n}$，…， $\frac{\sum_{i=1}^nx_{id}}{n}$) $\Rightarrow$ $w^T\overline{x}$（式1.4）

同理可得坏零件的均值

$w^T\overline{x^,}$ （式1.5）

所以类别的中心点之间的距离可以通过下列式子进行刻画

（ $w^T\overline{x}-$ $w^T\overline{x^,}$）² $\Rightarrow$ $w^T$ $(\overline{x}-$ $\overline{x^,})$ $(\overline{x}-$ $\overline{x^,})^T$ $w$ (式1.6)

如何刻画投影后相同类别的散乱程度

对于好零件来说，令 $x_i$表示（ $x_{i1}$, $x_{i2}$,…, $x_{id}$），投影后的方差为：

$\sum_{i=1}^n(\sum_{j=1}^nw_jx_{ij}-w^T\overline{x})^2$ $\Rightarrow$ $\sum_{i=1}^n(w^Tx_i-w^T\overline{x})^2$ $\Rightarrow$ $\sum_{i=1}^n(w^T(x_i-\overline{x})(x_i-\overline{x})^Tw)$

由于矩阵的加法与乘法满足分配率，所以上式可以变为：

$w^T(\sum_{i=1}^n(x_i-\overline{x})(x_i-\overline{x})^T))w$ (式1.7)

同理可得坏零件投影后的的方差为

$w^T(\sum_{i=1}^n(x_i^,-\overline{x^,})(x_i^,-\overline{x^,})^T))w$ (式1.8)

将式1.7与式1.8相加得：

$w^T(\sum_{i=1}^n(x_i-\overline{x})(x_i-\overline{x})^T))w+$ $w^T(\sum_{i=1}^n(x_i^,-\overline{x^,})(x_i^,-\overline{x^,})^T))w$
$\Downarrow$
$w^T(\sum_{i=1}^n(x_i^,-\overline{x^,})(x_i^,-\overline{x^,})^T+\sum_{i=1}^n(x_i-\overline{x})(x_i-\overline{x})^T)w$ （式1.9）

可以得出，式1.9最小时，有式1.7最小化，式1.8最小化

如何用式1.9与式1.6刻画LDA的两个关键点

$w^T$ $(\overline{x}-$ $\overline{x^,})$ $(\overline{x}-$ $\overline{x^,})^T$ $w$ (式1.6)

$w^T(\sum_{i=1}^n(x_i^,-\overline{x^,})(x_i^,-\overline{x^,})^T+\sum_{i=1}^n(x_i-\overline{x})(x_i-\overline{x})^T)w$ （式1.9）

令 $S_b$表示 $(\overline{x}-$ $\overline{x^,})$ $(\overline{x}-$ $\overline{x^,})^T$， $S_w$表示 $(\sum_{i=1}^n(x_i^,-\overline{x^,})(x_i^,-\overline{x^,})^T+\sum_{i=1}^n(x_i-\overline{x})(x_i-\overline{x})^T)$,先明确一点， $S_b$与 $S_w$均为标量， $S_b$为类间散度矩阵， $S_w$为类内散度矩阵

线性判别分析具有的两个关键点为

• 1、投影后，不同类别的点尽可能远离，令式1.6最大化
• 2、投影后，相同类别的点尽可能靠近，令式1.9最小化

因此，线性判别法的最终关键点为求下列函数的最大值

$J=\frac{w^TS_bw}{w^TS_ww}$

好，很好，现在已经将问题转换为函数极值问题了，这里使用拉格朗日乘子法求解，我们将分母限制为长度为1（这是用拉格朗日乘子法一个很重要的技巧），则有：

$c=w^TS_bw- \lambda(w^TS_ww-1)$

其实函数c长这个样子：

$c=S_b(w_1^2+w_2^2+....+w_d^2)-\lambda[S_w(w_1^2+w_2^2+....+w_d^2)]$，函数 $s$对 $w$求偏导有：

$\frac{\partial c}{\partial w_1}=2w_1S_b-2\lambda w_1S_w$
$\frac{\partial c}{\partial w_2}=2w_2S_b-2\lambda w_2S_w$
…
$\frac{\partial c}{\partial w_d}=2w_1S_b-2\lambda w_1S_w$

令上面这些式子等于0，其实等价于：

$2S_bw-2\lambda S_ww=0\Rightarrow S_bw=\lambda S_ww$

仔细观察， $S_bw$其实为

$(\overline{x}-$ $\overline{x^,})$ $(\overline{x}-$ $\overline{x^,})^Tw$

$(\overline{x}-$ $\overline{x^,})^Tw$为标量，我们设它为 $\lambda_w$，则有

$\lambda_w$ $(\overline{x}-$ $\overline{x^,})=\lambda S_ww$ $\Rightarrow$ $S_w^{-1}(\overline{x}-$ $\overline{x^,})=\frac{\lambda}{\lambda w}w$

其实 $S_w^{-1}(\overline{x}-$ $\overline{x^,})$就是最优解，假设 $w_1$是最优解，则 $S_w^{-1}(\overline{x}-$ $\overline{x^,})$为 $\frac{\lambda}{\lambda w}w_1$，我们把 $\frac{\lambda}{\lambda w}w_1$代入函数 $J$，会发现参数 $\frac{\lambda}{\lambda w}$被约掉了，所以 $S_w^{-1}(\overline{x}-$ $\overline{x^,})$就是最优解