题解 UVa11529

题目大意 多组数据，每组数据给定一个正整数 \(n(n\leq 1200)\) 和平面内 \(n\) 个点的坐标，保证没有三点共线或两点重合。请求出平均每个三角形内部包含几个点。

分析因为 \(n\leq 1200\)，所以直接枚举每个三角形和每个点的 \(O(n^4)\) 的做法是不行的，我们考虑枚举每个点，统计其贡献。

对于每个我们枚举到的点（以下称为原点 \(O\)），直接枚举每个包含它三角形很困难，所以从反面出发，枚举每个不包含它的三角形。可以先枚举三角形的一个端点 \(A\)，那么不难看出，在这两点连线 \(OA\) 的同侧的另外两个点 \(B,C\) 与点 \(A\) 所构成的三角形 \(\triangle ABC\) 一定不包含原点 \(O\)（如下图）。两个点分别在两侧的时候也有可能会不包含原点，但这种情况一定在枚举到 \(B\) 或 \(C\) 的时候被考虑进去（图中就是枚举到 \(B\) 的时候），所以只考虑 \(OA\) 某一侧的点即可，我们可以直接统计直线 \(OA\) 的左侧的所有点数量。

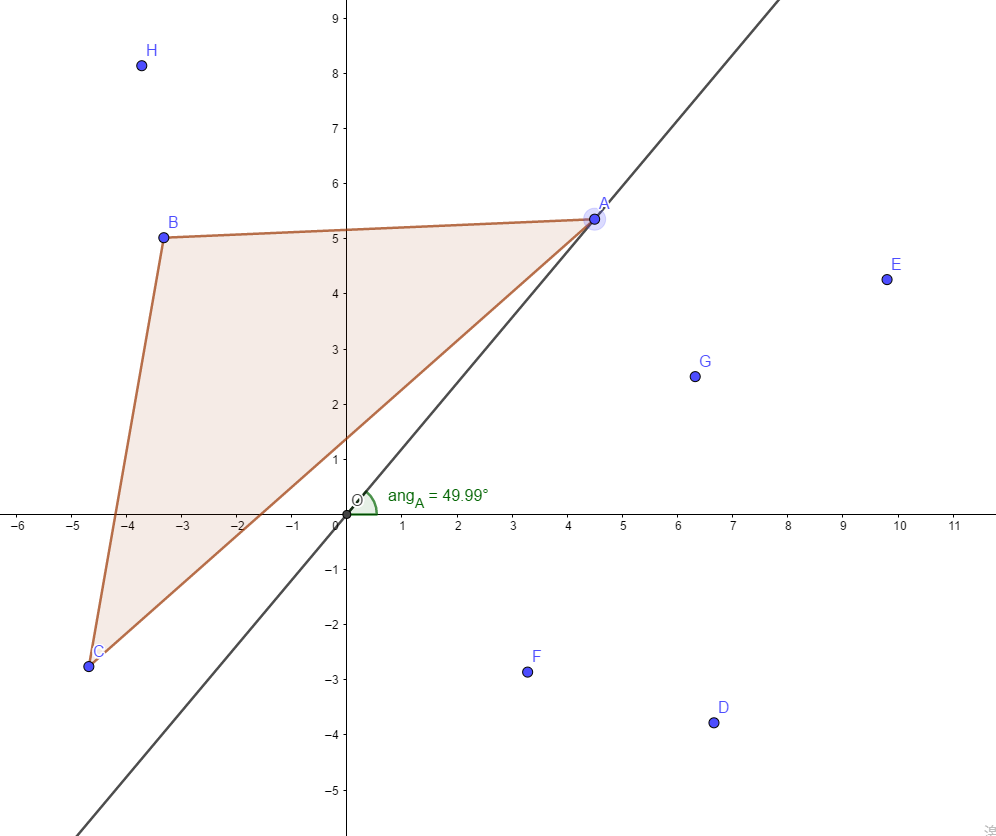
具体来说，我们对于当前枚举到的点 \(O\)，将其他点关于它的极角计算出来，对这些极角排序，然后再依次枚举每个极角 \(ang_A\)，将极角在 \([ang_A, ang_A+\pi]\) 的所有其它极角统计出来。仔细观察发现在统计极角时，由于极角满足单调性，所以不会再增加复杂度，最后的总复杂度为 \(O(n^2\log n)\)。特别注意，计算极角时，要把每个极角和它加上 \(2\pi\) 都计算进去，因为可能之后枚举到的极角加上 \(\pi\) 后超过 \(2\pi\)（比如 \(A\) 就在直线 \(OF\) 的一侧）。

#include<bits/stdc++.h>
using namespace std;

typedef long long ll;
const int maxn = 1205;
const double PI = acos(-1);

ll n, t, tot, now, ans;
double ang[maxn * 2];
struct Point {
    ll x, y;
} p[maxn];

ll C(ll n, ll m)
{
    ll res = 1;
    for(int i = 1; i <= m; ++i)
        res = res * (n - i + 1) / i;
    return res; 
}

int count(int x)
{
    ll res = 0;
    
    tot = 0, now = 1;
    for(int i = 1; i <= n; ++i) {
        if(i == x) continue;
        else {
            ang[++tot] = atan2(p[i].y - p[x].y, p[i].x - p[x].x);
            ang[tot + n - 1] = ang[tot] + 2 * PI;
        }
    }
    
    sort(ang + 1, ang + 2 * tot + 1);
    
    for(int i = 1; i <= tot; ++i) {
        while(ang[now] < ang[i] + PI) ++now;
        res += (now - i - 1) * (now - i - 2) / 2;
    }
    
    return C(n - 1, 3) - res;
}

int main()
{
    while(~scanf("%lld", &n) && n) {
        ans = 0;
        
        for(int i = 1; i <= n; ++i)
            scanf("%lld%lld", &p[i].x, &p[i].y);
        
        for(int i = 1; i <= n; ++i)
            ans += count(i);
        
        printf("City %d: %.2f\n", ++t, ans * 1.0 / C(n, 3));
    }
}

猜你喜欢