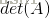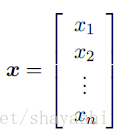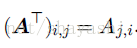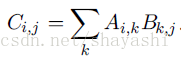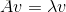Linear Algebra 线性代数
最近在看Deep Learning这本书,刚看了Linear Algebra章,总结一下。
名词函数
Scalars:标量,就是单个数,一般用小写倾斜字体表示。
Vectors:向量,一般用小写加粗字体表示。
Matrices:二维矩阵,一般用大写加粗字体表示。
Tensors:多维矩阵。
矩阵的基本运算
transpose:转置,使用右上标T表示转置。
乘法:C = AB
同时向量有点积运算,运算结果是标量而非向量。
矩阵满足结合律和交换律。
矩阵的逆
这本书里面矩阵的逆讲的很好,先从矩阵和向量的乘法引出矩阵的逆,然后将矩阵和向量的乘法,看做是从原点到向量b 的方法,将矩阵A 看做方向,那么x 就是我们在每个方向的前进的距离,从而引出了列空间的概念。列空间即通过A 可以到达的范围。所以Ax = b 是否有没有解等同于b 是否在A的列空间中。若A是m行n列的,则n一定要大于等于m,因为若n小于m,则b是n维的,不能构造出m维的b。这里引出了线性无关的概念,从而得出矩阵必须包含至少m个线性无关的列。因为矩阵只有一个逆矩阵,所以矩阵的行列数相同,否则,包含多个解。(我是觉得这一块论证的很好,所以简单翻译了一下,,这是我自己的理解,感兴趣的可以自己看一下原文)
Norms
范数是衡量向量的大小。Lp范数如下:
其中若p等于2,就是我们常用的欧几里得范数,即向量到原点的距离。
书中提到L0范数是不正确的术语(L0范数是向量中非零元素的个数),因为按比例扩大缩小数据不会改变非零元素的个数,但该向量被改变。
特殊类型的矩阵和向量
Diagonal Matrix(对角矩阵):对角矩阵是除了i = j以外的元素全为0的矩阵。
使用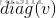

Symmetric Matrix(对称矩阵):对称矩阵是指矩阵等于该矩阵的转置矩阵: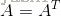
unit vector(单位向量):单位向量是满足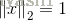
Orthogonal matrix(正交矩阵):正交矩阵是方形矩阵,且其行(列)互相正交。即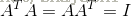
Eigendecomposition特征分解
特征分解就是讲矩阵分解成特征值(eigenvalue)和特征向量(eigenvector)的集合。
特征向量是满足下面式子的非零向量:
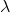
假设矩阵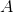
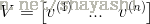
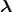
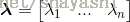
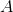
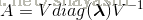
任意实对称(real symmetric)矩阵都可以被分解为实数域上的特征向量和特征值: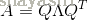
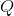
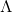
Singular Value Decomposition奇异值分解
只有方阵能进行特征分解,为了分解一般实矩阵,提出了SVD。奇异值分解写成: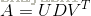
Moore-Penrose Pseudoinverse
摩尔-彭若斯广义逆 ,广义逆也成为伪逆,是处理非正方形的矩阵的逆矩阵。矩阵A的广义逆被定义为: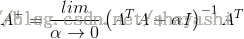
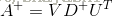
Determinant行列式
方阵的行列式记做