【编译原理笔记04】语法分析：自顶向下的分析概述、文法转换、LL1文法

本次笔记内容：
4-1 自顶向下分析概述
4-2 文法转换
4-3 LL1文法

自顶向下分析概述

• 从分析树的顶部（根节点）向底部（叶节点）方向构造分析树；
• 可以看成是从文法开始符号S推导出词串w的过程，例子如下。

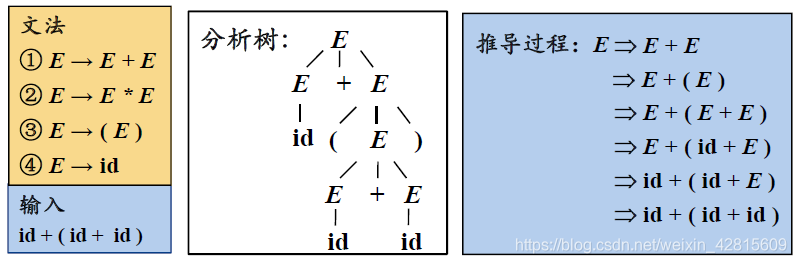
如上图，根据输入，选择文法的候选式，逐步推导出分析树。

每一步推导中，都需要做两个选择：

• 替换当前句型中的哪个非终结符；
• 用该非终结符的哪个候选式进行替换。

最左推导（Left-most Derivation）

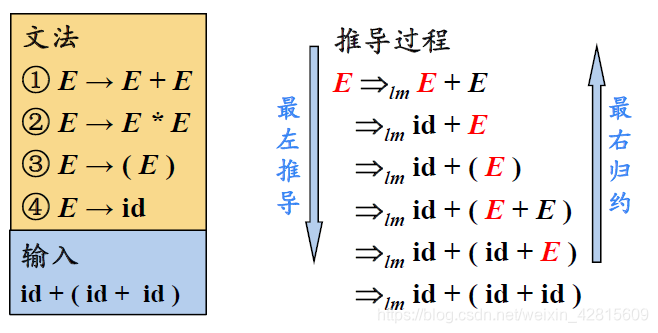
• 如上图，在最左推导中，总是选择每个句型的最左非终结符进行替换；
• 如果 $S \Rightarrow^*_{l m} \alpha$，则称α是当前文法的最左句型(left-sentential form)。

最右推导（Right-most Derivation）

• 如上图，在最右推导中，总是选择每个句型的最右非终结符进行替换；
• 在自底向上的分析中，总是采用最左归约的方式，因此把最左归约称为规范归约，而最右推导相应地称为规范推导。

最左推导和最右推导的唯一性

一个句子可能有很多推导方式，但最左推导和最右推导的结果都是唯一的。

自顶向下的语法分析采用最左推导方式

• 总是选择每个句型的最左非终结符进行替换；
• 根据输入流中的下一个终结符，选择最左非终结符的一个候选式。

例子如下：

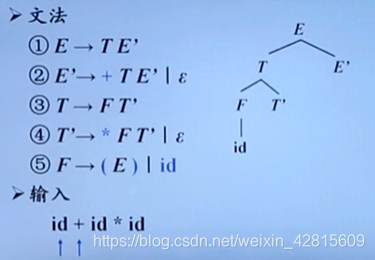
如上图，要匹配输入句子如id + id * id，构造分析树如图。指针指向id时（id下的蓝色箭头），发现F可以与id匹配，则将id匹配，并且指针后移，指向加号。

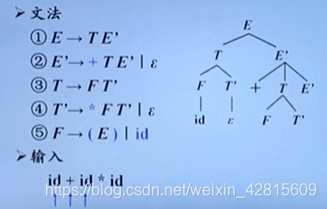
如上图，接下来选择T’的候选式，因为T’的候选式是以*开头的，因此不匹配，T’选择第二个候选式，即空epsilon。

而E’候选式以+开头，与指针所指的加号匹配，因此将E’展开为(+ T E’)，此时加号匹配，将指针后移，指向id。

轮到T选择候选式，选择(F T’)，以此类推。

结果如下。

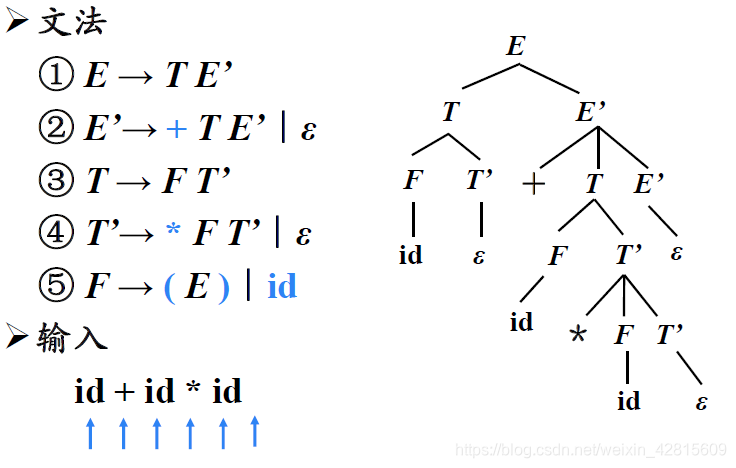
可见，恰好自动识别从左到右的句子。

自顶向下语法分析的通用形式

递归下降分析(Recursive-Descent Parsing)

• 由一组过程组成，每个过程对应一个非终结符；
• 从文法开始符号S对应的过程开始，其中递归调用文法中其它非终结符对应的过程。如果S对应的过程体恰好扫描了整个输入串，则成功完成语法分析；

• 如果不成功，则进行回溯（backtracking），尝试其他过程，从而导致效率较低。
• 预测分析不需要回溯。

预测分析(Predictive Parsing)

• 预测分析是递归下降分析技术的一个特例，通过
  在输入中向前看固定个数（通常是一个）符号来选
  择正确的A-产生式；
• 可以对某些文法构造出向前看k个输入符号的预测分析器，该类文法有时也称为LL(k) 文法类；
• 预测分析不需要回溯，是一种确定的自顶向下分析方法。

文法转换

自顶向下分析会遇到问题

非终结符多个候选式存在共同前缀导致回溯

左递归文法会使递归下降分析器陷入无限循环

• 含有A→Aα形式产生式的文法称为是直接左递归的(immediate left recursive)；
• 如果一个文法中有一个非终结符A使得对某个串α存在一个推导 $A \Rightarrow^* A \alpha$，那么这个文法就是左递归的；
• 经过两步或两步以上推导产生的左递归称为是间接左递归的。

消除直接左递归

对于左递归： $A \rightarrow A \alpha | \beta(\alpha \neq \varepsilon, \beta 不以A开头)$，可以进行如下推导：

$\begin{aligned} &A \Rightarrow A \alpha\\ &\begin{array}{l} {\quad \Rightarrow A \alpha \alpha} \\ {\quad \Rightarrow A \alpha \alpha \alpha} \\ {\quad \ldots} \\ {\quad \Rightarrow A \alpha \ldots \alpha} \\ {\quad \Rightarrow \beta \alpha \ldots \alpha} \end{array} \end{aligned}$

因为A可以直接替换成 $\beta$，因此，上式可以写成 $r=\beta \alpha^*$， $\alpha$个数可以为0。

因此，A可以定义成 $A \rightarrow \beta A'$，即以 $\beta$开头的表达式。其中 $A'$为新引入的非终结符， $A'$的定义可以为： $A' \rightarrow \alpha A' | \epsilon$。

因此，可以如下推导：

$\begin{aligned} &A' \Rightarrow \alpha A'\\ &\begin{array}{l} {\quad \Rightarrow \alpha \alpha A'} \\ {\quad \Rightarrow \alpha \alpha \alpha A'} \\ {\quad \ldots} \\ {\quad \Rightarrow \alpha \ldots \alpha A'} \\ {\quad \Rightarrow \alpha \ldots \alpha} \end{array} \end{aligned}$

在最后一步中，将 $A'$替换成空串。

事实上，这种消除过程就是把左递归转换成了右递归。

例子如下。

消除直接左递归的一般形式

消除左递归是要付出代价的——引进了一些非终结符和ε_产生式。

消除间接左递归

如上图中例子，消除间接左递归，即带入后，转换为直接左递归，再消除。

消除左递归算法

• 输入：不含循环推导（即形如 $A\Rightarrow^+ A$的推导）和ε-产生式的文法G
• 输出：等价的无左递归文法

提取公因子(Left Factoring)

对于上文中“非终结符多个候选式存在共同前缀导致回溯”产生的问题，使用提取公因子算法解决。

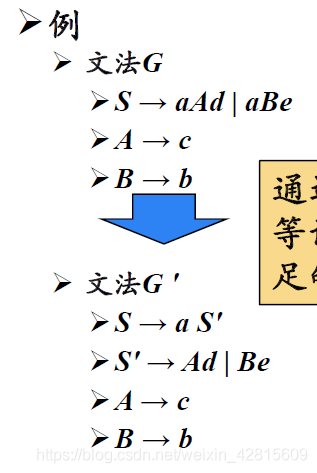
如上图，即通过改写产生式来推迟决定，等读入了足够多的输入，获得足够信息后再做出正确的选择。

算法如下。

• 输入：文法G
• 输出：等价的提取了左公因子的文法

LL(1)文法

预测分析法的工作过程为：从文法开始符号出发，在每一步推导过程中根据当前句型的最左非终结符A和当前输入符号a，选择正确的A-产生式。为保证分析的确定性，选出的候选式必须是唯一的。

什么文法能使用预测分析技术呢？

S_文法

S_文法(简单的确定性文法，Korenjak & Hopcroft，1966)提出，满足以下两个条件可以进行预测分析法：

• 每个产生式的右部都以终结符开始；
• 同一非终结符的各个候选式的首终结符都不同。

可以看出，S_中文法不含空产生式，这就限制了其应用。

什么时候使用ε产生式

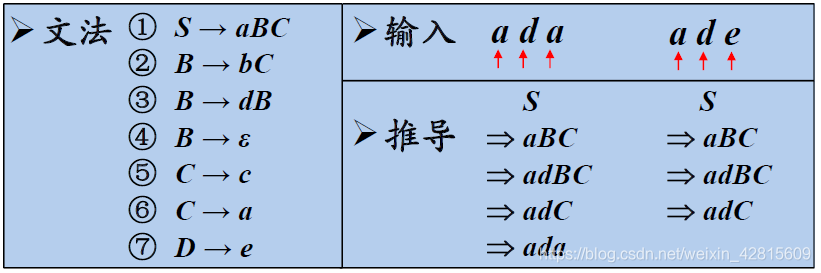
如上图，随意使用了空产生式④后，ada可以得到正确结果，但是ade却无法推导成功。

因此引出问题，什么时候使用ε产生式？

• 首先观察上图中文法，发现可以紧跟B后面出现的终结符有：c、a；
• 如果当前某非终结符A与当前输入符a不匹配时，若存在A→ε，可以通过检查a是否可以出现在A的后面，来决定是否使用产生式A→ε（若文法中无A→ε ，则应报错）。

由此引入非终结符的后继符号集的概念。

非终结符的后继符号集

非终结符A的后继符号集：可能在某个句型中紧跟在A后边的终结符a的集合，记为FOLLOW(A)。

$\boldsymbol{F O L L O W}(\boldsymbol{A})=\left\{\boldsymbol{a} | \boldsymbol{S} \Rightarrow^{*} \alpha \boldsymbol{A} a \boldsymbol{\beta}, \boldsymbol{a} \in \boldsymbol{V}_{T}, \quad \alpha, \boldsymbol{\beta} \in\left(\boldsymbol{V}_{T} \cup \boldsymbol{V}_{N}\right)^{*}\right\}$

如果A是某个句型的的最右符号，则将结束符“$”添加到FOLLOW(A)中。

例子如下。

如图，只有当前输入符号位a或c时（属于B的FOLLOW集时），才使用候选式(4)。

因此，引入产生式的可选集概念。

产生式的可选集与q_文法

产生式A→β的可选集是指可以选用该产生式进行推导时对应的输入符号的集合，记为SELECT( A→β )。例如：

• SELECT( A→aβ ) = { a }
• SELECT( A→ε ) = FOLLOW( A )

输入符号为a时，选择候选产生式A→aβ；输入符号属于FOLLOW( A )时，选择候选产生式A→ε。

由此，引出q_文法概念：

• 每个产生式的右部或为ε ，或以终结符开始；
• 具有相同左部的产生式有不相交的可选集。

但是，q_文法不含右部以非终结符打头的产生式。这就限制了其应用，引入LL(1)文法。

LL(1)文法

引入LL(1)文法，概念更加灵活，但是运算复杂度增加。

首先看串首终结符集概念。

串首终结符集

串首终结符即，串首第一个符号，并且是终结符，简称首终结符。

• 给定一个文法符号串α， α的串首终结符集FIRST(α)被定义为可以从α推导出的所有串首终结符构成的集合。如果 $\alpha \Rightarrow^* \epsilon$，那么ε也在FIRST(α)中：
• 对于 $\forall a \in (V_T \cup V_N)^*$， $\boldsymbol{F O L L O W}(\boldsymbol{A})=\left\{\boldsymbol{a} | \boldsymbol{S} \Rightarrow^{*} \alpha \beta, \boldsymbol{a} \in \boldsymbol{V}_{T}, \quad \alpha, \boldsymbol{\beta} \in\left(\boldsymbol{V}_{T} \cup \boldsymbol{V}_{N}\right)^{*}\right\}$；
• 如果 $\alpha \Rightarrow^* \epsilon$，那么ε∈FIRST(α)。

则重新定义产生式A→α的可选集SELECT：

• 如果 $\epsilon \notin FIRST(\alpha)$, 那么SELECT(A→α)= FIRST(α)
• 如果 $\epsilon \in FIRST(\alpha)$, 那么SELECT(A→α)=( FIRST(α)-{ε} )∪FOLLOW(A)。

LL(1)文法

文法G是LL(1)的，当且仅当G的任意两个具有相同左部的产生式A → α | β 满足下面的条件：

• 如果α 和β均不能推导出ε ，则FIRST(α)∩FIRST(β) =Φ；
• α 和β至多有一个能推导出ε；
• 如果 $\beta \Rightarrow^* \epsilon$，则FIRST (α)∩FOLLOW(A) =Φ（不相交）；
  如果 $\alpha \Rightarrow^* \epsilon$，则FIRST (β)∩FOLLOW(A) =Φ（不相交）。

即：

• 同一非终结符的各个产生式的可选集互不相交；
• 可以为LL(1)文法构造预测分析器。

LL(1)指：

• 第一个“L”表示从左向右扫描输入；
• 第二个“ L”表示产生最左推导；
• “1”表示在每一步中只需要向前看一个输入符号来决定语法分析动作。