DFT性质

DFT性质

线性

$DFT[ax_1(n)+bx_2(n)]=a\cdot DFT[x_1(n)]+b\cdot DFT[x_2(n)]$

圆周位移

说到圆周位移,就必须了解DFS是什么,而DFS与DFT之间又有什么关系.

DFS就是周期序列的离散傅里叶级数,对于周期为N的离散序列,DFS将对应N个独立谐波分量.

而DFT是取周期序列的主值周期进行DFS,所以我们可以看到,其实DFT是隐含周期性的,即使我们的取值超出了主值区间,但是还是有对应函数值的.

$DFS[\tilde{x}(n+m)]=e^{j\frac{2\pi}{N}mk} \tilde{X}(k)$

所谓圆周卷积就是说:对主值周期进行m点位移操作后,频率响应只有一个 $e^{j(\frac{2\pi}{N}k)}m$的线性位移,不影响其幅频特性.

证明如下:

已知
$\tilde{X}(k)=\sum_{n=0}^{N-1} \tilde{x}(n)e^{j\frac{2\pi}{N}nk}$
则对于 $\tilde{x}(n+m)$有
$\sum_{n=0}^{N-1} \tilde{x}(n+m)e^{j\frac{2\pi}{N}nk}$
令 $i=n+m$则 $n=i-m$,换元换限
$\sum_{i=m}^{N+m-1} \tilde{x}(i)e^{j\frac{2\pi}{N}k(i-m)}= e^{-j\frac{2\pi}{N}mk}\sum_{i=m}^{N+m-1} \tilde{x}(i)e^{j\frac{2\pi}{N}ki}$
结合已知即可得出
$DFS[\tilde{x}(n+m)]=e^{-j\frac{2\pi}{N}mk}\tilde{X}(k)$

在反变换中也有类似的性质
$IDFT[\tilde{X}(n+m)]=e^{j\frac{2\pi}{N}mk} \tilde{x}(k+m)$

表示离散时域的调制等效于离散频域的圆周位移

圆周卷积

把DFS的周期卷积中序列的在时间轴上移位过程，对应为在序列主值区间上的N个点的圆周移位.

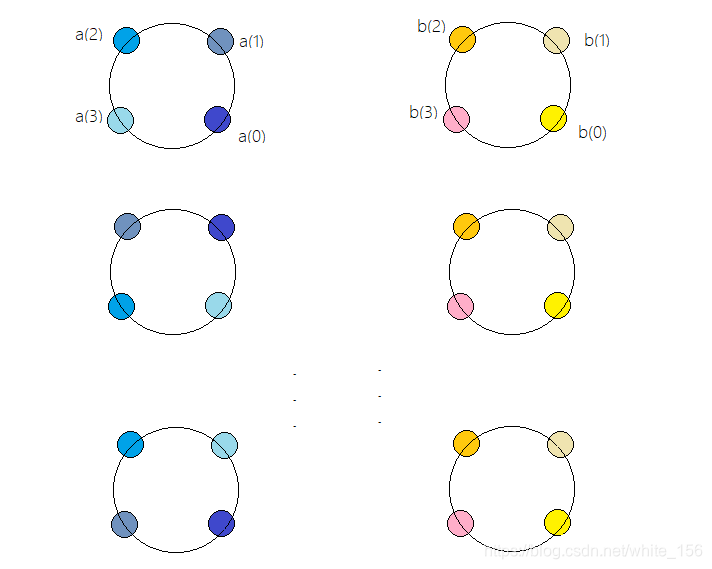
采用矩阵的形式实现,因此就需要规定做圆周卷积的长度L.如果序列长度不足L,则补零¹后进行计算.
$\begin{bmatrix} y(0) \\ y(1) \\ \vdots \\ y(L) \end{bmatrix}= \begin{bmatrix} b(0) & b(L-1) & b(L-2) & \cdots & b(1) \\ b(1) & b(0) & b(L-1) & \cdots & b(2) \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ b(L-1) & b(L-2) & b(L-3) & \cdots & b(0) \end{bmatrix} \begin{bmatrix} a(0) \\ a(1) \\ \vdots \\ a(L) \end{bmatrix}$

圆周卷积与线性卷积关系

L点圆周卷积是线性卷积以L为周期延拓后混叠相加序列的主值序列

由于L与 $N_1+N_2-1=N$的关系不定,又有如下三种情况:

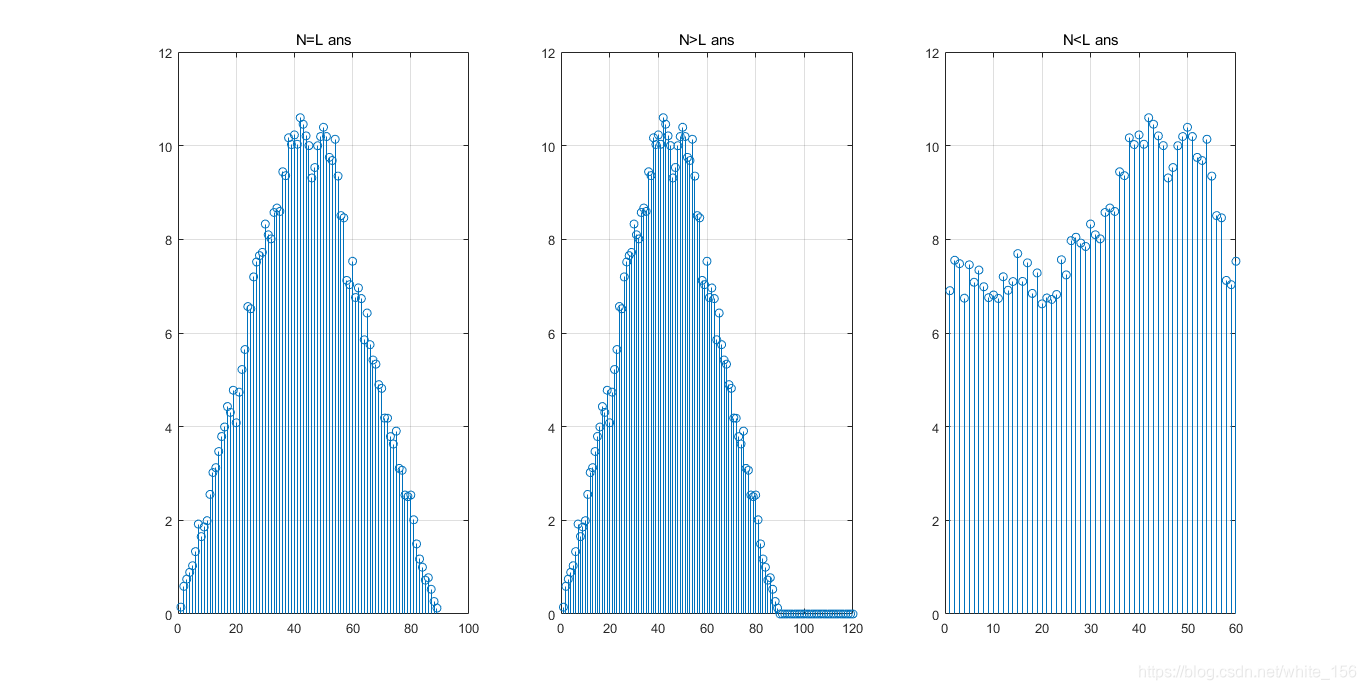
1. L=N
   此时L点圆周卷积与线性卷积的结果相同

2. L>N
   由于圆周卷积长度L大于线性卷积长度N,多余点数无定义,因而结果是线性卷积的补零序列

3. L<N
   由于是对线性卷积周期延拓的混叠相加,所以在这种情况下必然导致两相邻周期部分混叠,在主值周期内只有在区间 $[N-L,L-1]$区间内的值没有混叠,与线性卷积结果相同,其他都不准确.

---

1. 补零又分为尾补零和头补零,补零方式不同影响结果中补零位置. ↩︎