题解
更好的阅读体验点击这里
,请各位大佬到我的blog看看。
知识点:
后缀树,后缀数组,LCP,树形DP
分析:
这道题是我初学后缀结构的近期训练最后一道练习题,一开始只想到\(\Theta(n^2)\)的方法和“不存在10相似”的情况。后来看了一年前wj哥哥的slide,才知道真正的做法。
这道题的题意是这样的:我们要求出有多少个子串的LCP大于等于每个\(i\in [1,n]\)中的\(i\),第二问要求出每个组当中\(a[i]\)值两两乘积中最大的一个是多少(而且\(a[i]\in \mathbb Z\),也就是说有可能有非正数)。我们发现直接做LCP大于等于的情况很不好写,所以先考虑求出等于的情况,而第二问也不算核心,直接用一个DP记录一下就好了,可以先放一放。
下面先简介两种方法:
方法一:后缀数组
第一问实际上是求有多少个区间\([l,r]使得height[l..r]的最小值为i\),然后我们考虑用并查集维护后缀集合,从\(n-1\)到\(0\)枚举每一个可能的后缀长度\(i\),在此之前,每个集合内部的任意两个后缀的\(LCP\) 都大于\(i\)。这时假如有两个排名相邻的并且\(LCP\) 为$i $的后缀,我们就可以把它们所处的集合合并起来。
具体地,把\(height\)值从大到小排个序,然后然后把\(ans[heght]\)的值加上当前合并的两个相邻的集合的大小乘积(因为根据乘法原理,每个区间中,依次枚举左右端点,是有乘积中情况)。然后合并集合。
记录的时候要注意,因为我们合并的时候都是合并排名相邻的一些后缀,所以出现在一个集合中的所有后缀必定是连续的,所以我们只需要记录每个集合的左右端点就可以了。合并的时候也只用更改端点的值就好了。
对于第二问,我们在合并的时候可以把\(a[i]\)的值也顺路合并(具体方法可见方法二,大同小异)。然后就做完了。
时间复杂度:\(\Theta(n\log_2n)\)
方法二:后缀树
把后缀树建出来之后,我们直观地发现LCP就变成了LCA(两个点的LCA节点在后缀树上对应的节点的长度值就是LCP的长度)。而每个子树下的后缀节点的个数,就是那棵树的贡献。
如图:
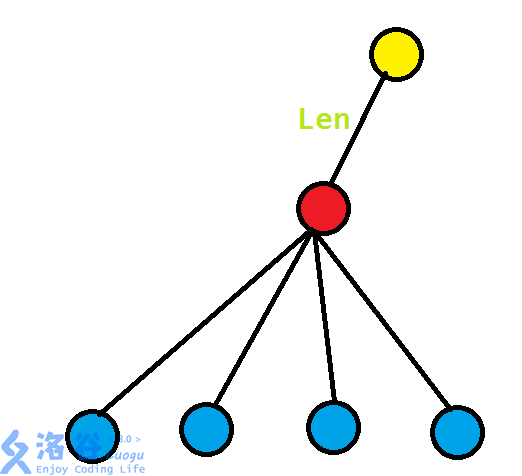
对于每个蓝点的子树统计好后缀节点的个数,然后对其LCA(红点)进行统计,然后途中的“len”就是他们LCP的长度(假设从红点往上一直走了很多个节点后到达了整棵后缀树的根节点(黄点),之间的距离(边权之和)就是len)。
具体地,我们可以先建出后缀树。然后进行树形DP(理解为DFS也行)。怎么统计后缀节点的个数呢?这个相当简单,只需要对其子节点的子树信息进行累加就可以了,而我们知道怎么样的节点才可能是后缀节点。在建树的时候,直接加进去的一定是后缀点,通过一条原来很长完整的边(里面包含不止一个字符的)的分裂得到的点,一定不是后缀点,这个在建树的时候判断一下就好了。但是答案一定是这个吗?
当然不是!
回到那幅图,考虑现在在红点统计答案。这时候的单位贡献就是\(len\),小学数学告诉我们:\(单位贡献\times数量=总共贡献\),所以我们现在统计数量。数量是有多少个后缀节点对(无序的)产生的贡献,考虑对蓝色点标号\(1,2,3,\cdots,k\),每个蓝点为子树(包含蓝点,就是说假如蓝点是后缀点,那也算进去)的总共后缀节点数为\(v_1,v_2,v_3,\cdots,v_k\),那么对于红点的贡献数量就是\(\displaystyle\sum_{i=1}^{k-1}\sum_{j=i+1}^{k}v_i\times v_j\),这样可以保证不重不漏(大家可以把那四个蓝点的情况直接写出来,看一下对不对,我当时推的式子是\(v_1\times v_2+v_1\times v_3+v_1\times v_4+v_2\times v_3+v_2\times v_4+v_3\times v_4\)),可以发现它我上面给出的双重和式的意义是一样的。
但是这个式子求出来的最大复杂度是\(\Theta(n^2)\)的,所以一定不可以通过。
考虑对式子进行展开,先对原式\(\times2\),然后再\(\div2\),
第一步,我们得到\(\text{原式}=\frac{\displaystyle\sum_{i=1}^{k}\sum_{j=1\land j\not =i}^{k}v_i\times v_j}{2}\)(举例,就是\(\frac{v_1\times(v_2+v_3+v_4)+v_2\times(v_1+v_3+v_4)+v_3\times(v_1+v_2+v_4)+v_4\times(v_1+v_2+v_3)}{2}\))
第二步,我们发现这个式子好像差了点什么,所以继续添加项,添加为\(v_1\times(v_1+v_2+v_3+v_4)\),在这里我们多加了一个\(v_1^2\),所以把它减去。此时假如大家把后面几项也这样拆开,就可发现后面都是\((v_1+v_2+v_3+v_4)\),前面是\(v_i\times\)后面的那个括号。初中数学告诉我们,我们应该合并同类项,变成\((v_1+v_2+v_3+v_4)^2\),这样,就是非常简便的了。
第三步,对第二步的式子进行化简,写成原式\(=\frac{(\displaystyle\sum_{i=1}^{k}{v_i})^2-\displaystyle\sum_{i=1}^{k}{v_i^2}}{2}\)
然后这个式子就可以\(\Theta(n)\)的时间内求出来,可以接受(具体操作就是对于每一个子节点求一次和与一次平方和就好了)。这种推式子的方法好像和很多题解的方法不同,但是本质要求都是一样的。
对于第二问,我们要设法更新\(a[i]\)的最大值。因为此题中\(a[i]\)的值是可正可负的,所以就不可以只记录每个节点下的最大和次大值。参照我去年做过的一道环形DP题(【IOI1998】Polygon)中的思想,同时记录下最大和次大与最小和次小值。因为如果最小和次小值是个负数,两者相乘会变成一个正数,这个正数的有可能比最大值和次大值的乘积要大,所以可以用这个来更新答案。
不过千万注意,一定要弄懂其中的逻辑关系。这里计算出来的值(最小次小的乘积,最大次大的乘积)都只是用来更新\(ans[len]\)的,而合并到父节点(上图的红点)的信息,依旧是原来的最大最小等等的值(就是更新答案的时候一直都是用原来的信息,不是乘积)。所以说,我们一直用原有的信息去更新每一个值,而不是计算后更新。
具体地,初始化一定要做好。把每个后缀节点的初始最大最小值设为\(a[i]\),而次大次小分别设成负无穷和正无穷。加入非后缀节点时(分裂节点),把四个值分别设成正负无穷(因为这些节点本来就需要别的点去更新它们,它们自己本来就没有权值)。而什么东西都没有的根节点,也要设成正负无穷。在树形DP的时候,假如我们需要更新父节点\(u\)的信息,当前枚举到的子节点是\(v\),我们就可以把\(u\)和\(v\)的最大最小次大次小拿出来,大的排一遍序,取最大那两个更新\(u\)节点的信息。对于小的值同理,也是拿出来排一遍序,然后取最小的两个放回去。此处经过计算可得,冒泡排序是理论上计算次数相对少的而写起来又很方便的一种排序,每一次更新只用12次的运算(远远小于快排),所以常数会小很多。不过看到有一种可以直接更新的方法,就是分别比较两个最值,然后直接往后更新,感觉这种好像更快,但是当时我觉得写这种好像风险有点大,怕写WA。如果当前的统计完发现整棵子树的大小小于2,那么就可以离开了,因为构不成两两之间的 LCP了,这样没法更新答案(不过子树大小还是要更新的,后面有用)。
最后的求一次后缀和与后缀最大值,就从后面往前更新(因为题目说\(r\)相似的两个串同时也是\(r-i\)相似的),所以假如当前的后缀和还是\(0\),那么就把最大值也设成\(0\)(在计算过程中,最大值有可能是一些不可预知的数)。然后注意细节,注意更新的顺序。
时间复杂度:\(\Theta(n)\)
小结:
对比两种不同的方法,其实本质上是相同的。方法一中合并\(height\)的过程就是模拟了后缀树上两两合并LCA的过程,只不过树形结构更加便于理解和实践。两种方法各有优劣,但是理论复杂度上后缀树会更佳一些。实现上,方法一难在第一问的合并(好像挺难写的),方法二难在第二问的统计\(a[i]\)的答案和细节调错上,毕竟树形结构难以调试,细节超多。不用后缀自动机解题的原因是,后缀自动机想起来没有后缀树好想,但是实现起来却与后缀树大同小异,还要用\(parents\)树进行再一次的转化,没有这个必要,毕竟树的性质是比DAG要多的,要更为方便的。
代码:
这道题我一共交了四次才AC。我用的是方法二(感觉更好写)。
可以看见其实细节很多。我觉得对于更新第二问的答案时是最为麻烦的。大家千万小心。
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int maxn=300010;
typedef long long ll;
int n,m,tot,cnt,tp,rt,head[maxn<<1];//注意节点数会变成2n,所以存树的时候也一定要开这么大的空间
ll b[maxn];//这个是题目中给出的a[i]
const ll inf=1000000007;//事实证明INF要开到比1e9大才可以
char s[maxn];
struct node
{
int fa,p,len,siz;//父亲,当前位置,后缀长度,子树大小
ll _min1,_max1,_min2,_max2;//最小,最大,次小,次大
int trans[27];
}a[maxn<<1];
struct data
{
int nxt,to;
}edge[maxn<<1];//存树,边只用开2n就够了,因为只需要用单向边来存父亲到儿子就好了
struct result
{
ll sum,val;//后缀节点的对数,最大值
}ans[maxn];//记录答案
#define min(a,b) (a<b?a:b)//最小
#define max(a,b) (a>b?a:b)//最大
#define isdigit(c) (c>=48&&c<=57)//判断是否是数字,用于读入优化
#define swap(a,b) (a^=b^=a^=b)//交换
ll read()
{
ll x=0,f=1;
char c=getchar();
while (!isdigit(c))
f=c=='-'?-1:1,c=getchar();
while (isdigit(c))
x=(x<<1)+(x<<3)+(c^48),c=getchar();
return x*f;
}
int ins(int u,int p,int c)//建后缀树
{
int x=++tot,v;
a[x].len=a[u].len+1;
a[x].p=p;
a[x].siz=1;//这一定是后缀点
a[x]._min1=a[x]._max1=b[p];//注意最小最大赋值成a[i]
a[x]._min2=inf;//其余赋值成正负无穷
a[x]._max2=-inf;
for (;u&&!a[u].trans[c];a[u].trans[c]=x,u=a[u].fa);
if (!u)
a[x].fa=rt;
else
{
v=a[u].trans[c];
if (a[v].len==a[u].len+1)
a[x].fa=v;
else
{
int w=++tot;
a[w]=a[v];
a[w].len=a[u].len+1;
a[w]._max1=a[w]._max2=-inf;//分裂点没有权值,只能被别人更新,所以初始为正负无穷
a[w]._min1=a[w]._min2=inf;
a[w].siz=0;//分裂点一定不是后缀点
a[v].fa=a[x].fa=w;
for (;u&&a[u].trans[c]==v;a[u].trans[c]=w,u=a[u].fa);
}
}
return x;
}
void cmp(int u,int v)//用来更新最大最小次大次小值,u是父亲,v是儿子
{
int i,j;
ll p[10];
memset(p,0,sizeof(p));
p[1]=a[u]._max1;
p[2]=a[u]._max2;
p[3]=a[v]._max1;
p[4]=a[v]._max2;
for (i=1;i<=3;i++)//冒泡
for (j=1;j<=4-i;j++)
if (p[j]<p[j+1])
swap(p[j],p[j+1]);
a[u]._max1=p[1];
a[u]._max2=p[2];
memset(p,0,sizeof(p));
p[1]=a[u]._min1;
p[2]=a[u]._min2;
p[3]=a[v]._min1;
p[4]=a[v]._min2;
for (i=1;i<=3;i++)
for (j=1;j<=4-i;j++)
if (p[j]>p[j+1])
swap(p[j],p[j+1]);
a[u]._min1=p[1];
a[u]._min2=p[2];
}
void dfs(int u)//树形DP统计答案
{
int i,v;
ll tmp=0;//tmp是每个子树的节点个数的平方之和
for (i=head[u];i;i=edge[i].nxt)
{
v=edge[i].to;
dfs(v);
a[u].siz+=a[v].siz;//加上子树大小
tmp+=(a[v].siz+0ll)*(a[v].siz+0ll);//记录平方和
cmp(u,v);//统计最大最小值
}
if (a[u].siz<2)//构不成LCP就返回
return;
ans[a[u].len].sum+=((a[u].siz+0ll)*(a[u].siz+0ll)-tmp)/2ll;//记录有多少点对
ans[a[u].len].val=max(ans[a[u].len].val,max((a[u]._max1*a[u]._max2),(a[u]._min1*a[u]._min2)));//记录此处的乘积最大值
}
void add(int u,int v)//把树形结构建立起来
{
edge[++cnt]=(data){head[u],v};
head[u]=cnt;
}
int main()
{
int i,j;
scanf("%d%s",&n,s+1);
for (i=1;i<=n;i++)
b[i]=read();
rt=tp=++tot;
for (i=n;i>=1;i--)
{
tp=ins(tp,i,s[i]-'a'+1);
ans[i].val=-(inf*inf);//初始化每个节点,注意是要INF的平方才行(因为这个是乘积)
}
for (i=2;i<=tot;i++)
add(a[i].fa,i);//建边
a[rt]._min1=a[rt]._min2=inf;
a[rt]._max1=a[rt]._max2=-inf; //根节点要更新
dfs(rt);//树形DP
for (i=n-1;i>=0;i--)//统计后缀和、后缀最大值
{
if (ans[i].sum==0)//如果当前为0,那么全都为0
ans[i].val=0;
if (i<=n-2&&ans[i+1].sum!=0)//上一个不为0,可以用来更新
ans[i].val=max(ans[i].val,ans[i+1].val);
ans[i].sum+=ans[i+1].sum;//更新和
}
for (i=0;i<=n-1;i++)
printf("%lld %lld\n",ans[i].sum,ans[i].val);
return 0;
}然后我又交到的UOJ上,发现被人Hack掉了。
in:
2
aa
1000000000 -1000000000
out:
1 -1000000000000000000
1 -1000000000000000000这样的数据可以慢慢调,总能搞好的。
总结:
这是我人生第一道洛谷黑题啊!
虽然用了一天去写,但也感觉很值得。
思路很有趣,很多的实现细节也很有价值。