边界对图像来说是至关重要的信息,人可以仅通过图像边缘、轮廓就能对图像整体产生较完整的认识,例如漫画、简笔画等待。基于边界的图像分割技术是基于灰度不连续性进行的分割方法,其基础就是边缘检测
边缘检测
利用梯度、差分、拉普拉斯算子及高通滤波等处理方法进行图像锐化,增强图像边缘,再进行一次阈值化处理,便可以将边缘增强的方法用于边缘检测
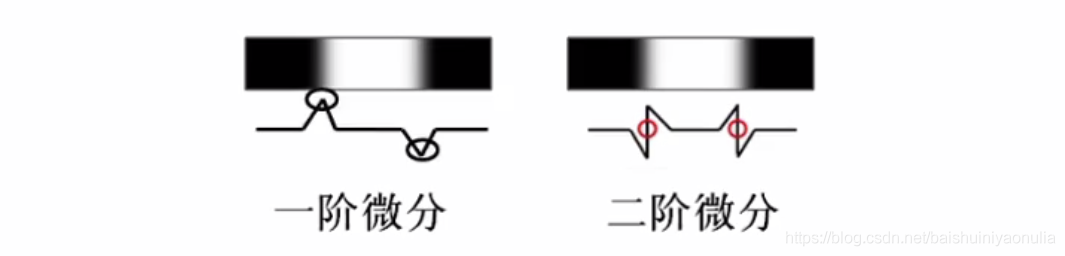
部分常用的边缘检测算子处理效果展示
- 梯度算子
∇f=[GxGy]=⎣⎡∂x∂F∂y∂F⎦⎤
- Roberts算子
[100−1][0−110]
- Prewitt算子
⎣⎡−1−1−1000111⎦⎤⎣⎡10−110−110−1⎦⎤
- Sobel算子
⎣⎡−1−2−1000121⎦⎤⎣⎡10−120−210−1⎦⎤

边缘连接
由于噪声的原因,边界的特征很少能够被完整地描述,在亮度不一致的地方会中断。典型的边缘检测算法后面总要跟随着连接过程和其他边界检测过程,用来规整边界像素,成为有意义的边界。
简单来说大概有两类方法:
1、局部处理法
1.1 基本原理:
对做过边缘检测的图像的每个点
(x,y)的特性在一个小的邻域中进行分析,所有相似的点被连接形成一个享有共同特性像素的边界。
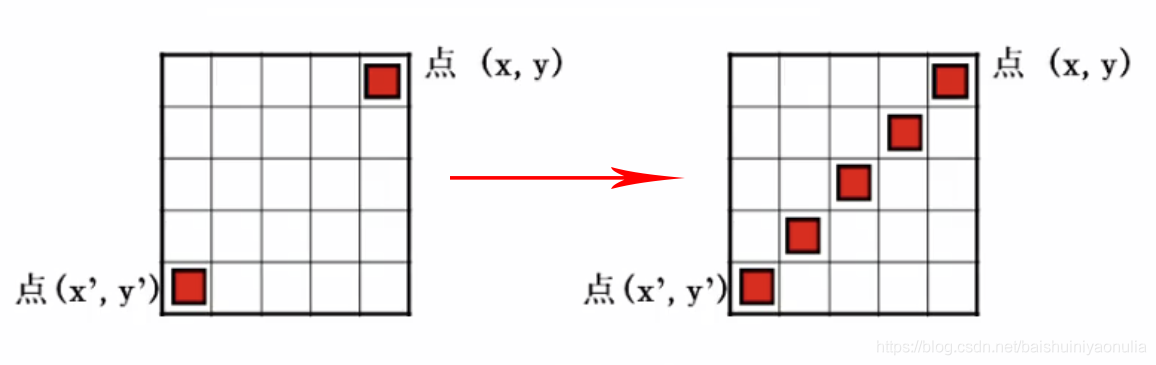
所分析的特性一般是像素之间梯度算子的响应强度和梯度方向
- 通过比较梯度强度确定两个点之间的连接性:
对于点
(x′,y′),判断其是否与领域内的点
(x,y)相似,当
∣∇f(x,y)−∇f(x′,y′)∣⩽T时可以判定两个像素之间的梯度强度相近。
- 通过比较梯度方向确定两个点之间的连接性:
对于点
(x′,y′),判断其是否与领域内的点
(x,y)的方向角相似,当
∣α(x,y)−α(x′,y′)∣⩽T时可以判定两个像素之间的有相互连接的趋势。
若梯度强度和梯度方向都小于所设置的阈值,则可以说像素
(x,y)和
(x′,y′)是连接的
1.2 边缘跟踪:
将检测的边缘点连接成线,形成有意义的边界。
- 光栅跟踪
采用电视光栅行扫描顺序,结合阈值检测,对遇到的像素进行分析从而确定是否为边缘的跟踪方法,具体步骤如下:
(1) 选取一个较大的检测阈值
d,对图像第一行进行阈值化。大于
d的像素作为对象点,并作为下一步跟踪的起始点
(2) 选取一个较小的跟踪阈值
k,例如灰度差阈值
(3) 扫描下一行像素(像素
(i,j)的下一行像素
(i+1,j−1)、
(i+1,j)、
(i+1,j+1)为跟踪邻域),凡与上一行对象点相邻接的像素灰度差小于
k的且值最小的点接受为新对象点,反之去除
(4) 对未被接受为对象点的其他各行像素再次从步骤(1)开始重复
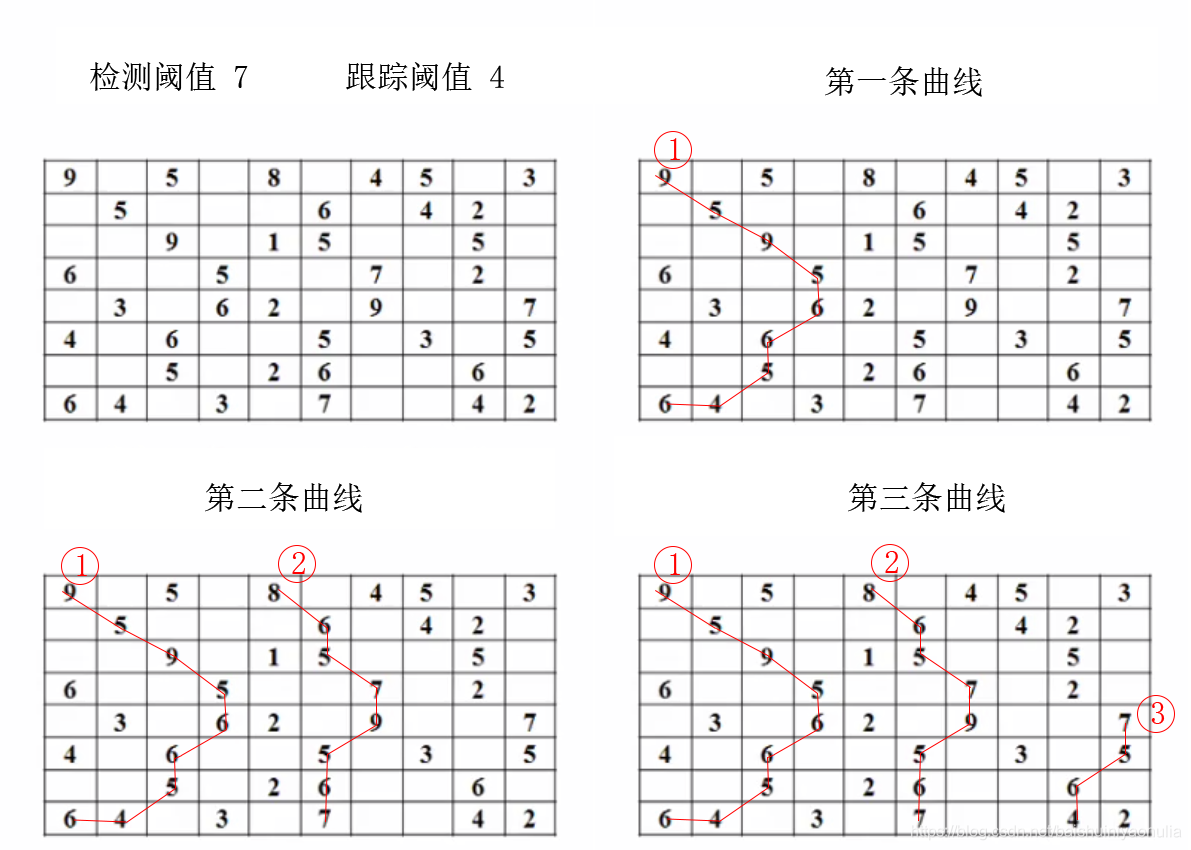
- 全向跟踪
全向跟踪是指跟踪方向可以是任意方向,并且有足够大的跟踪距离的跟踪方法。是一种改变了邻域定义和跟踪准则的光栅跟踪法,其跟踪步骤和原则与光栅跟踪法一致
(1) 邻域:选取适当的、能进行全向跟踪的邻域,例如八邻域等
(2) 跟踪准则:选择一个适当的跟踪准则,如灰度阈值、对比度和空间距离等
2、Hough变换
在找出边界点集之后,需要连接形成完整有意义的边界图像描述。在预先知道区域形状的条件下,利用Hough变换不仅可以方便地得到边界曲线将不连续的像素点连接起来,而且可以用数学公式来表达该直线,性能优异。
基本思想: 对于边界上
n个点的点集,找出其满足形状的点集和曲线方程
这里介绍一下利用Hough变换检测直线边界的例子:
已知任意两点的直线方程
y=ax+b有一个未知数平面
xy和一个参数平面
ab,且在未知数平面上任一条直线
y=ax+b都在参数平面上对应着一个点。
那么可得,过未知数平面一个点
(x,y)的所有直线,构成参数平面上的一条直线
b=−ax+y显然这是一条参数平面上的直线方程
若有两点
(x1,y1)、
(x2,y2)且这两点在未知数平面上共线,那么这两点在参数平面上的直线将会交于
(a,b)点
{y1=ax1+by2=ax2+b→{b=−ax1+y1b=−ax2+y2据此可以推断,在未知数平面上共线的点最终都会交于参数平面上的
(a,b)点,因此若在参数平面上有多条直线相交于某一个点,则该点的坐标
(a,b)可以作为未知数平面上直线方程的参数,这样就检测出了这条直线边界。
Hough变换检测直线算法
- 在算法的实际使用过程中,为了避免出现无穷大,常用极坐标形式代替直角坐标形式。此时,参数平面就为
ρθ平面,而不是直角坐标下的
ab平面:
xcosθ+ysinθ=ρ

- 创建交点累加器或交点统计直方图,找出相交线最多的参数空间的点
- 找出该点对应的未知数平面的直线线段,即检测完成
实例:

Hough变换的扩展
- 检测圆
将Hough变换应用到对圆的检测上时,其参数方程变换为
(x−c1)2+(y−c2)2=c32此时需要三个参数的参数空间
- 检测椭圆
参数方程设为
a2(x−x0)2+b2(y−y0)2=1微分后有
a2x−x0+b2y−y0⋅dxdy=0微分后的方程只有三个独立参数,只需从
(a,b,x0,y0)中选择三个参数进行检测即可






