声明:本文参考https://blog.csdn.net/u013733326/article/details/79702148,记录学习过程中的心得体会
Python版本:3.6.x
实验目的:搭建一个能分类平面数据的浅层神经网络,它只有一个隐藏层
在这篇文章中,我们会学到以下知识:
- 构建具有单隐藏层的二分类神经网络
- 了解非线性激活函数,如tanh函数
- 计算损失函数
- 编程实现前向传播和后向传播
实验步骤:
一、加载、处理数据
开始前引入的库:

import numpy as np import matplotlib.pyplot as plt import sklearn import sklearn.datasets import sklearn.linear_model from testCases import * from planar_utils import plot_decision_boundary, sigmoid, load_planar_dataset, load_extra_datasets
- sklearn:进行数据挖掘和数据分析的框架
- testCases:提供一些测试样例评估函数的正确性
- planar_utils:提供在本实验中使用的功能函数
加载、查看数据集:

X, Y = load_planar_dataset() plt.scatter(X[0,:], X[1,:], c = np.squeeze(Y), s = 40, cmap = plt.cm.Spectral) #s表示大小,c表示颜色序列,cmap表示Colormap plt.show()

shape_X = X.shape #(2,400) shape_Y = Y.shape #(1,400) m = Y.shape[1] #训练集里面的数量 print ("X的维度为: " + str(shape_X)) print ("Y的维度为: " + str(shape_Y)) print ("数据集里面的数据有:" + str(m) + " 个") X的维度为: (2, 400) Y的维度为: (1, 400) 数据集里面的数据有:400 个
符号说明:
- X:(2,400)的numpy矩阵,包含数据点的数值
- Y:(1,400)的numpy向量,对应X的标签(0-red、1-blue)
二、搭建浅层神经网络
浅层神经网路的模型如下图:
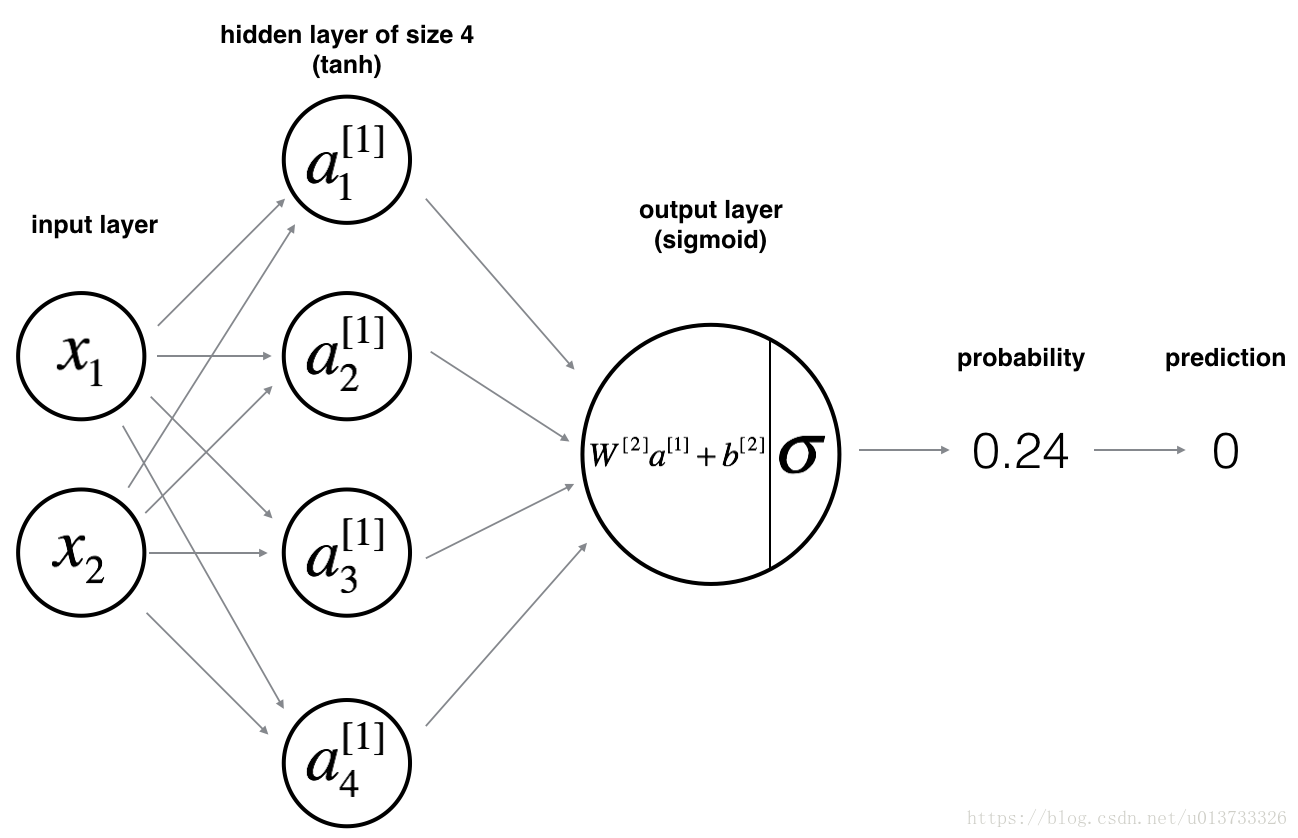
前向传播:
对单个样本$\left \{ x^{\left ( i \right )},y^{\left ( i \right )}\right \}$:
隐藏层中每个神经元的计算过程如下:
$$\left\{\begin{matrix}
z_{1}^{\left [ 1 \right ]}=w_{1}^{\left [ 1 \right ]}x + b_{1}^{\left [ 1 \right ]} &a_{1}^{\left [ 1 \right ]}=\sigma \left ( z_{1}^{\left [ 1 \right ]} \right ) \\
z_{2}^{\left [ 1 \right ]}=w_{2}^{\left [ 1 \right ]}x + b_{2}^{\left [ 1 \right ]} &a_{2}^{\left [ 1 \right ]}=\sigma \left ( z_{2}^{\left [ 1 \right ]} \right )\\
z_{3}^{\left [ 1 \right ]}=w_{3}^{\left [ 1 \right ]}x + b_{3}^{\left [ 1 \right ]} &a_{3}^{\left [ 1 \right ]}=\sigma \left ( z_{3}^{\left [ 1 \right ]} \right ) \\
z_{4}^{\left [ 1 \right ]}=w_{4}^{\left [ 1 \right ]}x + b_{4}^{\left [ 1 \right ]} &a_{4}^{\left [ 1 \right ]}=\sigma \left ( z_{4}^{\left [ 1 \right ]} \right )
\end{matrix}\right.$$
$$\begin{align*}
z^{\left [ 1 \right ]}&=\begin{bmatrix}
z_{1}^{\left [ 1 \right ]}\\
z_{2}^{\left [ 1 \right ]}\\
z_{3}^{\left [ 1 \right ]}\\
z_{4}^{\left [ 1 \right ]}
\end{bmatrix}=\begin{bmatrix}
\cdots &W_{1}^{\left [ 1 \right ]T} & \cdots \\
\cdots &W_{2}^{\left [ 1 \right ]T} & \cdots \\
\cdots &W_{3}^{\left [ 1 \right ]T} &\cdots \\
\cdots &W_{4}^{\left [ 1 \right ]T} & \cdots
\end{bmatrix}\ast \begin{bmatrix}
x_{1}\\x_{2}
\end{bmatrix}+\begin{bmatrix}
b_{1}^{\left [ 1 \right ]}\\
b_{2}^{\left [ 1 \right ]}\\
b_{3}^{\left [ 1 \right ]}\\
b_{4}^{\left [ 1 \right ]}
\end{bmatrix}\\\\
z^{\left [ 1 \right ]}&=W^{\left [ 1 \right ]}x+b^{\left [ 1 \right ]}
\end{align*}$$
$$a^{\left [ 1 \right ]}=\begin{bmatrix}
a_{1}^{\left [ 1 \right ]}\\
a_{2}^{\left [ 1 \right ]}\\
a_{3}^{\left [ 1 \right ]}\\
a_{4}^{\left [ 1 \right ]}
\end{bmatrix}=\sigma \left ( \begin{bmatrix}
z_{1}^{\left [ 1 \right ]}\\
z_{2}^{\left [ 1 \right ]}\\
z_{3}^{\left [ 1 \right ]}\\
z_{4}^{\left [ 1 \right ]}
\end{bmatrix} \right )=\sigma \left ( z^{\left [ 1 \right ]} \right )$$
对于多个样本
$$X = \begin{bmatrix}
\vdots & \vdots & \vdots & \vdots \\
x^{\left ( 1 \right )} & x^{\left ( 2 \right )} & \cdots &x^{\left ( m \right )} \\
\vdots & \vdots & \vdots & \vdots
\end{bmatrix}$$
对于所有训练样本,需要让i从1到m实现下式:
$$z^{\left [ 1 \right ]\left ( i \right )}=W^{\left [ 1 \right ]}x^{\left ( i \right )}+b^{\left [ 1 \right ]}\\$$
$$a^{\left [ 1 \right ]\left ( i \right )}=\sigma \left ( z^{\left [ 1 \right ]\left ( i \right )} \right )$$
所以有
$$\begin{align*}
Z^{\left [ 1 \right ]} &= \begin{bmatrix}
\vdots & \vdots & \vdots & \vdots \\
z^{\left [ 1 \right ]\left ( 1 \right )} & z^{\left [ 1 \right ]\left ( 2 \right )} & \cdots &z^{\left [ 1 \right ]\left ( m \right )} \\
\vdots & \vdots & \vdots & \vdots
\end{bmatrix}\\&=\begin{bmatrix}
W^{\left [ 1 \right ]}x^{\left ( 1 \right )}+b^{\left [ 1 \right ]} &W^{\left [ 1 \right ]}x^{\left ( 2\right )}+b^{\left [ 1 \right ]} &\cdots & W^{\left [ 1 \right ]}x^{\left ( m \right )}+b^{\left [ 1 \right ]}
\end{bmatrix}\\&=W^{\left [ 1 \right ]}\begin{bmatrix}
x^{\left ( 1 \right )}&x^{\left ( 2\right )} &\cdots & x^{\left ( m \right )}
\end{bmatrix} +\begin{bmatrix}
b^{\left [ 1 \right ]} & b^{\left [ 1 \right ]} & \cdots & b^{\left [ 1 \right ]}
\end{bmatrix}\\&=W^{\left [ 1 \right ]}X+b^{\left [ 1 \right ]}(Python中的广播机制)
\end{align*}$$
$$\begin{align*}
A^{\left [ 1 \right ]}&=\begin{bmatrix}
\vdots &\vdots & \vdots &\vdots \\
a^{\left [ 1 \right ]\left ( 1 \right )}& a^{\left [ 1 \right ]\left ( 2 \right )} & \cdots & a^{\left [ 1 \right ]\left ( m \right )} \\
\vdots & \vdots &\vdots & \vdots
\end{bmatrix}=\begin{bmatrix}
\sigma \left ( z^{\left [ 1 \right ]\left ( 1 \right )} \right )& \sigma \left ( z^{\left [ 1 \right ]\left ( 2 \right )} \right ) &\cdots & \sigma \left ( z^{\left [ 1 \right ]\left ( m \right )} \right )
\end{bmatrix}\\&=\sigma \begin{bmatrix}
z ^{\left [ 1 \right ]\left ( 1 \right )}&z ^{\left [ 1 \right ]\left ( 2 \right )} &\cdots & z ^{\left [ 1 \right ]\left ( m \right )}
\end{bmatrix}=\sigma\left ( Z^{\left [ 1 \right ]} \right )
\end{align*}$$
反向传播
对于单个样例$\left \{ x,y \right \}$(省略上标):
$$\because z^{\left [ 2 \right ]}=W^{\left [ 2 \right ]}a^{\left [ 1 \right ]}+b^{\left [ 2 \right ]}\\$$
$$a^{\left [ 2 \right ]}=\sigma \left ( z^{\left [ 2 \right ]} \right )\\$$
$$\therefore dz^{\left [ 2 \right ]}=a^{\left [ 2 \right ]}-y\\$$
$$db^{\left [ 2 \right ]}=dz^{\left [ 2 \right ]}\\$$
$$dW^{\left [ 2 \right ]}=dz^{\left [ 2 \right ]}a^{\left [ 1 \right ]T}\Leftrightarrow \left ( n^{\left [ 2 \right ]},n^{\left [ 1 \right ]}\right )= \left ( n^{\left [ 2 \right ]} ,1 \right )*\left (1,n^{\left [ 1 \right ]}\right)\\$$
$$da^{\left [ 1 \right ]}=W^{\left [ 2 \right ]T}dz^{\left [ 2 \right ]}\Leftrightarrow \left ( n^{\left [ 1 \right ]},1 \right )=\left ( n^{\left [ 1 \right ]},n^{\left [ 2 \right ]} \right )*\left ( n^{\left [ 2 \right ]} ,1\right )\\$$
$$\because z^{\left [ 1 \right ]}=W^{\left [ 1 \right ]}a^{\left [ 0 \right ]}+b^{\left [ 1 \right ]}\left(a^{\left [ 0 \right ]}=x \right )\\$$
$$a^{\left [ 1 \right ]}=g^{\left [ 1 \right ]}\left ( z^{\left [ 1 \right ]} \right )\\$$
$$dz^{\left [ 1 \right ]}=da^{\left [ 1 \right ]}\ast g^{\left [ 1 \right ]}{}'\left ( z^{\left [ 1 \right ]} \right )=W^{\left [ 2 \right ]T}dz^{\left [ 2 \right ]}\ast g^{\left [ 1 \right ]}{}'\left ( z^{\left [ 1 \right ]} \right )\\$$
$$db^{\left [ 1 \right ]}=dz^{\left [ 1 \right ]}\\$$
$$dW^{\left [ 1 \right ]}=dz^{\left [ 1 \right ]}a^{\left [ 0 \right ]T}=dz^{\left [ 1 \right ]}x$$
对于全部样例$\left \{ X,Y \right \}$:
$$A^{\left [ 2 \right ]}=\begin{bmatrix}
\vdots & \vdots &\vdots &\vdots \\
a^{\left [ 2 \right ]\left ( 1 \right )}& a^{\left [ 2 \right ]\left ( 2 \right )} & \cdots &a^{\left [ 2 \right ]\left ( m \right )} \\
\vdots&\vdots & \vdots &\vdots
\end{bmatrix}\\$$
$$Y=\begin{bmatrix}
y^{\left ( 1 \right )} & y^{\left ( 2 \right )} & \cdots & y^{\left ( m \right )}
\end{bmatrix}\\$$
$$\begin{align*}
dZ^{\left [ 2 \right ]}&=\begin{bmatrix}
dz^{\left [ 2 \right ]\left ( 1 \right )}& dz^{\left [ 2 \right ]\left ( 2 \right )} & \cdots & dz^{\left [ 2 \right ]\left ( m \right )}
\end{bmatrix}\\&=\begin{bmatrix}
a^{\left [ 2 \right ]\left ( 1 \right )}-y^{\left ( 1 \right )} & a^{\left [ 2 \right ]\left ( 2 \right )}-y^{\left ( 2 \right )} &\cdots & a^{\left [ 2 \right ]\left ( m \right )}-y^{\left ( m\right )}
\end{bmatrix}\\ &=A^{\left [ 2 \right ]}-Y
\end{align*}$$
全部样例对W1的偏导数实际上是从1到m所有单个样例对W1偏导数的平均值:
$$\begin{align*}
dW^{\left [ 2 \right ]}&=\frac{1}{m}\sum_{i=1}^{m}dz^{\left [ 2 \right ]\left ( i \right )}a^{\left [ 1 \right ]\left ( i \right )T}=\frac{1}{m}\begin{bmatrix}
dz^{\left [ 2 \right ]\left ( 1 \right )}&\cdots & dz^{\left [ 2 \right ]\left ( m \right )}
\end{bmatrix}\begin{bmatrix}
a^{\left [ 1 \right ]\left ( 1 \right )T}\\
\cdots \\ a^{\left [ 1 \right ]\left ( m \right )T}
\end{bmatrix}\\
&=\frac{1}{m}\begin{bmatrix}
dz^{\left [ 2 \right ]\left ( 1 \right )} &\cdots & dz^{\left [ 2 \right ]\left ( m \right )}
\end{bmatrix}\begin{bmatrix}
a^{\left [ 1 \right ]\left ( 1 \right )} & \cdots &a^{\left [ 1 \right ]\left ( m \right )}
\end{bmatrix}^{T}=\frac{1}{m}np.dot\left ( dZ^{\left [ 2 \right ]},A^{\left [ 1 \right ]T} \right )
\end{align*}$$
$$db^{\left [ 2 \right ]}=\frac{1}{m}\sum_{i=1}^{m}dz^{\left [ 2 \right ]\left ( i \right )}=\frac{1}{m}np.sum\left ( dZ^{\left [ 2 \right ]},axis=1,keepdims=True \right )$$
注:axis=1,表示按照行取平均值
单个样例和全部样例的公式表格如下:

本篇未完,待续中......
