计算流体力学简介(二)——伪谱法

一维对流方程

$\frac{\partial u}{\partial t}+c\frac{\partial u}{\partial x}=0$ ，取 $c=1$ ，现用伪谱法求解 $\frac{\partial u}{\partial t}+\frac{\partial u}{\partial x}=0$ 。
初场为 $u_0(x)=e^{-x^2}，x\in[-5,5]$
空间精度取8阶
时间推进使用欧拉法，步长取0.1。
首先构造推进使用的离散方程
将 $u$ 的傅里叶展开 $u(x,t)=\sum a_i(t)e^{jw_ix}$
代入原方程
$\frac {\partial}{\partial t}\sum a_i(t)e^{jw_ix}+\frac {\partial}{\partial x}\sum a_i(t)e^{jw_ix}=0$
第二项可以直接求导得到
$\frac {\partial}{\partial t}\sum a_i(t)e^{jw_ix}+\sum jw_ia_i(t)e^{jw_ix}=0$
时间导数项使用一步R-K方法
得到
$\sum \frac{a^{n+1}_i-a^n_i}{\Delta t}e^{-jw_ix}+\sum jw_ia^n_ie^{jw_ix}=0$
由此得到谱系数更新公式
${a^{n+1}_i}=(1-j{\Delta t}w_i)a^n_i$
计算代码如下

#include <iostream>
#include <cmath>
#include <complex>
#include "fftw3.h"
using namespace std;
const int N=8,//空间点数(阶数)
NS=100;//时间步数
const double pi=atan(1)*4;
const double rb=-5,l=10,//计算域左边界，计算域长度
dt=0.1//时间步长
;
void init_guass(double* u0)//设置高斯函数初场
{
    for(int i=0;i<N;i++) 
	{
		u0[i]=exp(-pow((l*double(i)/(N-1)+rb),2));
	}
}
struct _tran//傅里叶变换的辅助类
{
	fftw_plan s2p,p2s;
	int n;
	_tran(int _n):n(_n)
	{
		double *up;
		fftw_complex *us;
		us  = (fftw_complex*)fftw_malloc(sizeof(fftw_complex)*n);
		up = (double*) fftw_malloc(sizeof(double)*n);
    	s2p = fftw_plan_dft_c2r_1d(n,us,up,FFTW_MEASURE);
	    p2s = fftw_plan_dft_r2c_1d(n,up,us,FFTW_MEASURE);
		fftw_free(us);
    	fftw_free(up);
	}
	void tran(double* in,fftw_complex* out)//正变换：物理空间到谱空间
	{
		fftw_execute_dft_r2c(p2s,in,out);
	}
	void itran(fftw_complex* in,double* out)//逆变换：谱空间到物理空间
	{
		fftw_execute_dft_c2r(s2p,in,out);
		for(int i=0;i<n;i++) out[i]/=n;
	}
	~_tran()
	{
		fftw_destroy_plan(p2s);
		fftw_destroy_plan(s2p);
	}
}fft(N),fft2(2*N);
void prt(fftw_complex* in)//输出谱系数
{
	for(int i=0;i<N/2+1;i++) cout<<*((complex<double>*)(&in[i]))<<'\t';
    cout<<endl;
}
void prt(double* in)//输出网格点上的值
{
	for(int i=0;i<N;i++) cout<<in[i]<<'\t';
    cout<<endl;
}
void advance(fftw_complex *us)//单步时间推进
{
	complex<double> *a=(complex<double>*)(us);
	for(int i=0;i<N/2+1;i++)
	{
		a[i]=(complex<double>(1,0)-complex<double>(i*dt*(2*pi/l),0)*complex<double>(0,1))*a[i];
	}
}
int main()
{
    fftw_complex *us;
    double *up;
	us  = (fftw_complex*)fftw_malloc(sizeof(fftw_complex)*N);
	up = (double*) fftw_malloc(sizeof(double)*N);
    init_guass(up);
	cout<<N<<'\t'<<NS<<'\t'<<rb<<'\t'<<l<<'\n';
	prt(up);
    fft.tran(up,us);
	for(int i=0;i<NS;i++)
	{
		advance(us);
		fft.itran(us,up);
		prt(up);
	}
	fftw_free(us);
    fftw_free(up);
    return 0;
}

这里利用fftw快速傅里叶变换库来做傅里叶变换。
结果如下
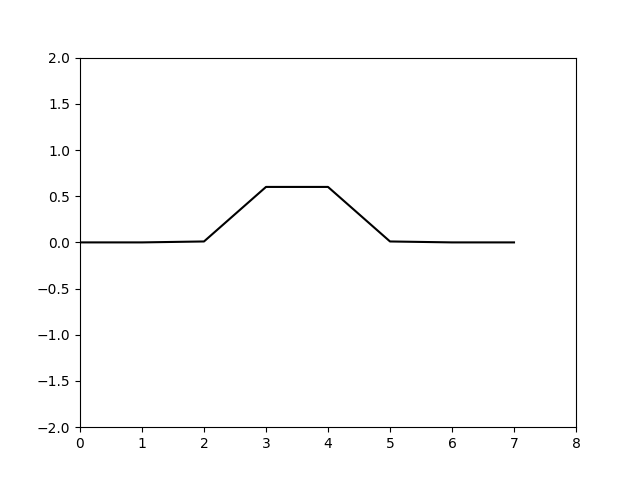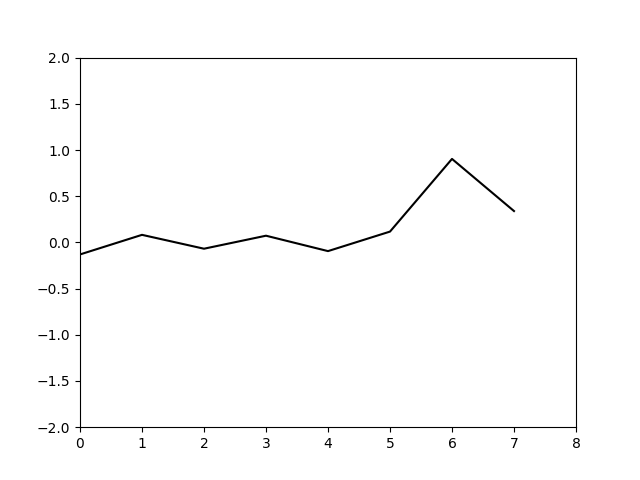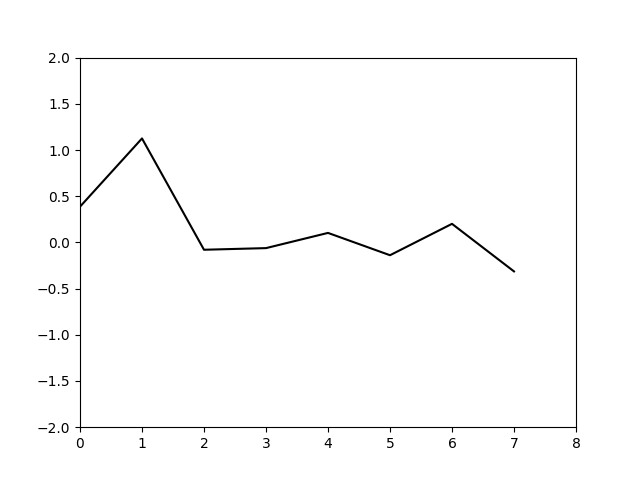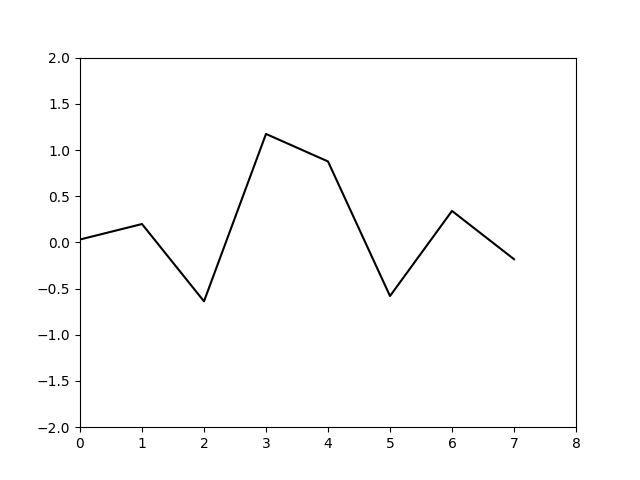
在这里插入图片描述
可以看到基本运动规律，这里仅仅是把网格点上的值输出出来绘制的图像，实际上可以利用三角函数插值将图像描绘的更精细，不过我懒得做了。
为了得到更精细的图像，我们加密空间网格，或者说提高阶数，将N改为32，再次计算绘制图像如下
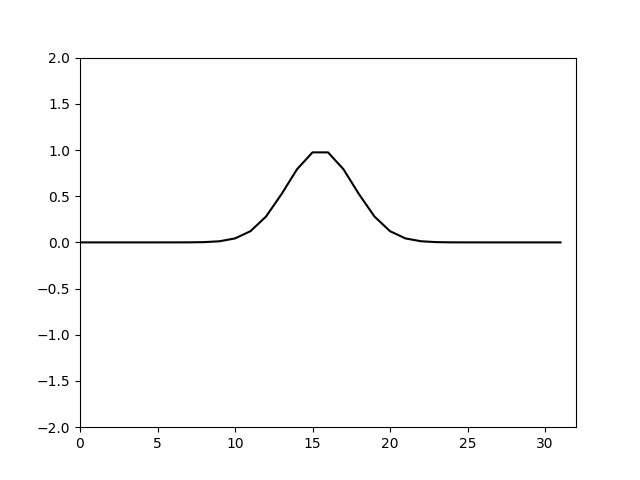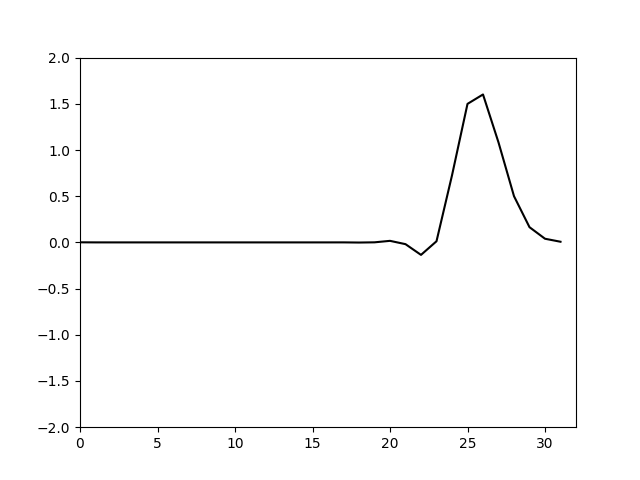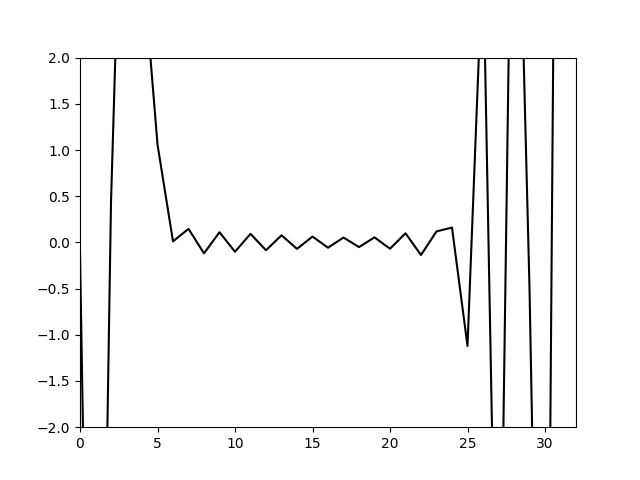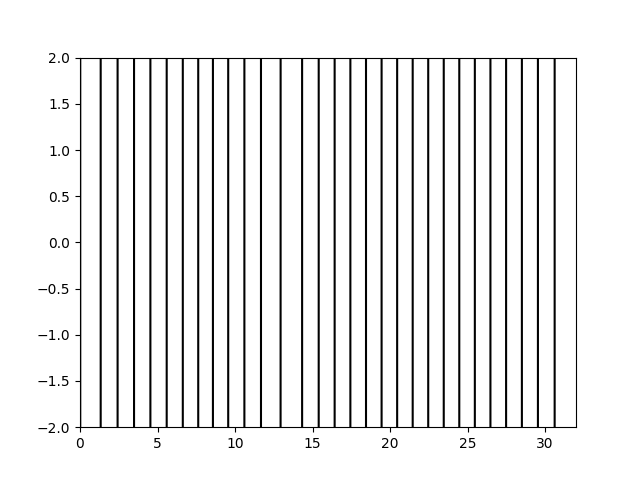
在这里插入图片描述
可以看到图像更为精细了，但是随着计算的推进波形的峰值逐渐增加，并且出现了异常的高频震荡。

考察谱系数递推公式
${a^{n+1}_i}=(1-j{\Delta t}w_i)a^n_i$
傅里叶变换的谱系数的模实际表示的是相应谐波分量的能量，因此我们考察递推过程中谱系数的模的变化规律
$\frac{|{a^{n+1}_i}|}{|a^n_i|}=|1-j{\Delta t}w_i|>1$
可以看到每一次推进，谱系数的模都会比上一步的谱系数更大，这就意味着随着时间的推进系统中的总能量是不断增加的，并且从公式的形式可以看到，谐波分量的频率越大，该分量的能量就增长的越快。

从两个计算结果也可以看到，8阶时计算100步，波形的峰值有缓慢增加，但并没有32阶时的明显发散。这就是因为8阶谐波分量的能量增长速度慢于32阶谐波分量。当空间上使用32阶精度计算时最高阶谐波的能量增长非常快，以至于很快就出现了网格点间的明显震荡，并且很快淹没了原始波形。这说明这种计算格式是不稳定的。

根据这一分析，我们就可以想办法抑制这种不稳定现象，既然谱系数推进时所乘的系数模大于1会使得系统总能量增大，最终造成计算发散，那么我们就强制让推进时乘的系数等于1不就能力守恒了。于是修改推进的公式为
${a^{n+1}_i}=\frac{(1-j{\Delta t}w_i)}{|1-j{\Delta t}w_i|}a^n_i$
于是我们得到新的advance函数

void advance(fftw_complex *us)//单步时间推进
{
	complex<double> *a=(complex<double>*)(us);
	for(int i=0;i<N/2+1;i++)
	{
        complex<double> t=(complex<double>(1,0)-complex<double>(i*dt*(2*pi/l),0)*complex<double>(0,1));
        t=t/complex<double>(abs(t),0);
		a[i]=t*a[i];
	}
}

用新的推进方法来计算，再次绘制图像得到
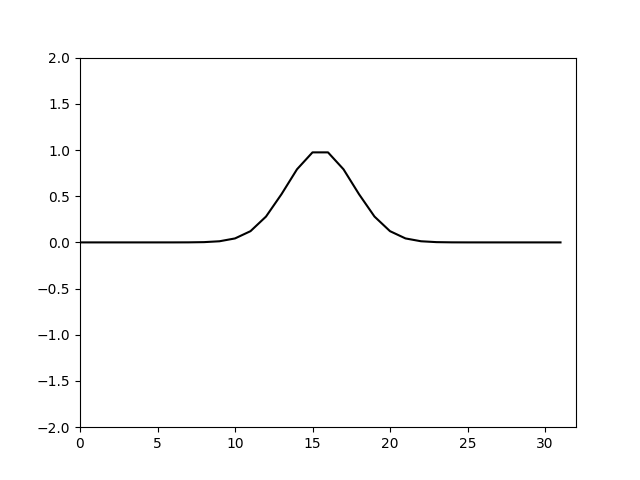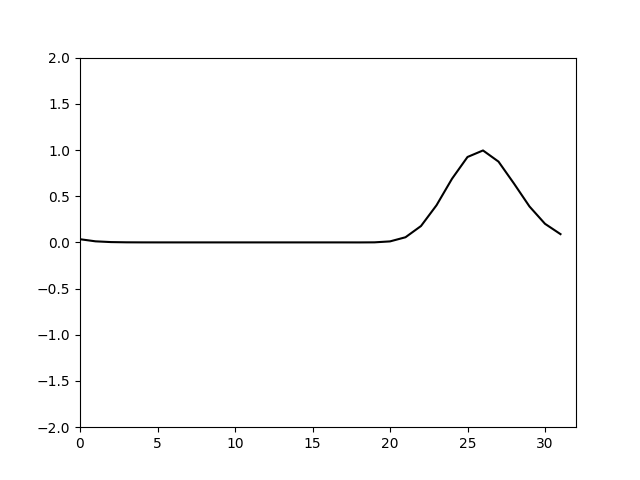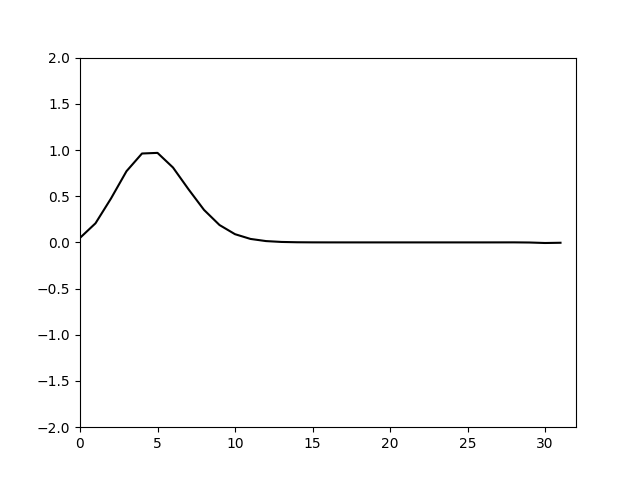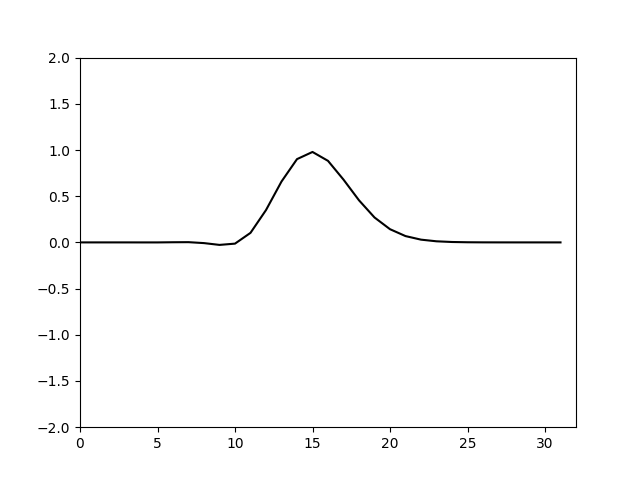
在这里插入图片描述
可以看到调整了推进系数就可以使计算不再发散而且和真解基本没有了差异。

无粘Burgers方程

$\frac{\partial u}{\partial t}+cu\frac{\partial u}{\partial x}=0$ ，取 $c=1$ ，现用伪谱法求解 $\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}=0$ 。
这个方程和对流方程的区别就是原本对流方程中的 $c$ 变成了 $cu$ 。这使得方程从线性方程变成了非线性方程。
同样构造离散公式。
初场为 $u_0(x)=e^{-x^2}，x\in[-5,5]$
空间精度取8阶
时间推进使用欧拉法，步长取0.1。
首先构造推进使用的离散方程
将 $u$ 的傅里叶展开 $u(x,t)=\sum a_i(t)e^{jw_ix}$
代入原方程
$\frac {\partial}{\partial t}\sum a_i(t)e^{jw_ix}+(\sum a_i(t)e^{jw_ix})\frac {\partial}{\partial x}\sum a_i(t)e^{jw_ix}=0$
第二项可以直接求导得到
$\frac {\partial}{\partial t}\sum a_i(t)e^{jw_ix}+(\sum a_i(t)e^{jw_ix})(\sum jw_ia_i(t)e^{jw_ix})=0$
这里要化简第二项就要计算卷积了，根据傅里叶变换的性质，卷积可以通过一次傅里叶变换变成直接相乘，因为快速傅里叶变换的存在，利用这种方式可以减小计算量。
时间导数项使用一步R-K方法
得到谱系数更新公式
${a^{n+1}_i}=a^n_i-(a^n_i)'$
其中 $(a^n_i)'$ 是卷积后的谱系数。
新的advance函数代码如下

void advance(fftw_complex *us)//单步时间推进
{
	complex<double> *a=(complex<double>*)(us);
    fftw_complex *ts=(fftw_complex*)fftw_malloc(sizeof(fftw_complex)*(N/2+1));
    double *tp=(double*)fftw_malloc(sizeof(double)*N),
    *tp2=(double*)fftw_malloc(sizeof(double)*N);
    for(int i=0;i<N/2+1;i++) 
    {
        *(complex<double>*)(&ts[i])=complex<double>(i*dt*(2*pi/l),0)*complex<double>(0,1)*a[i];
    }
    fft.itran(ts,tp);
    fft.itran(us,tp2);
    for(int i=0;i<N;i++) tp[i]*=tp2[i];
    fft.tran(tp,ts);
	for(int i=0;i<N/2+1;i++)
	{
		a[i]-=(*(complex<double>*)(&ts[i]));
	}
    fftw_free(ts);
    fftw_free(tp);
    fftw_free(tp2);
}

这时计算出的的结果如下
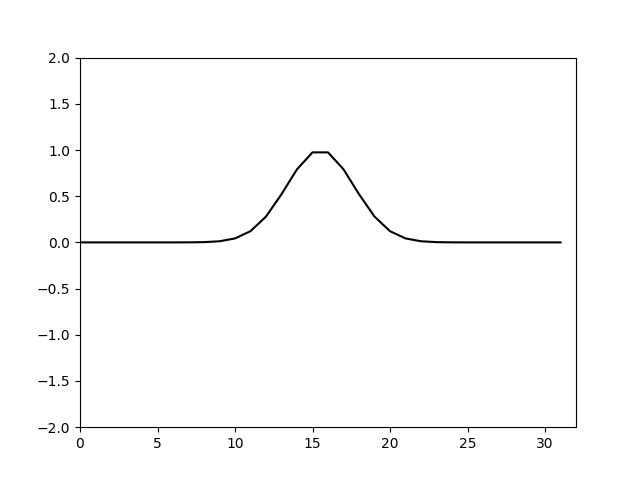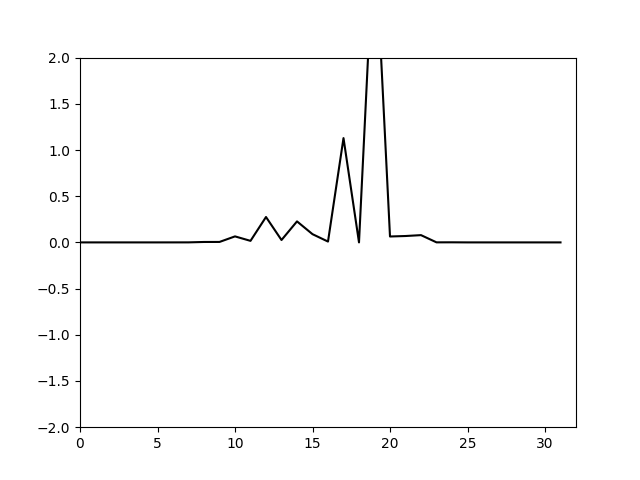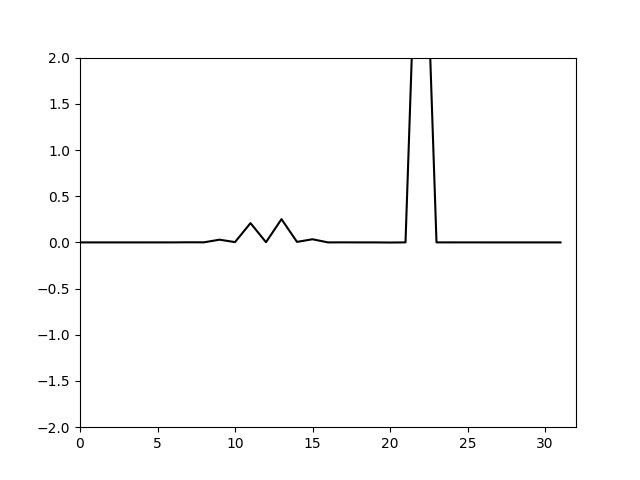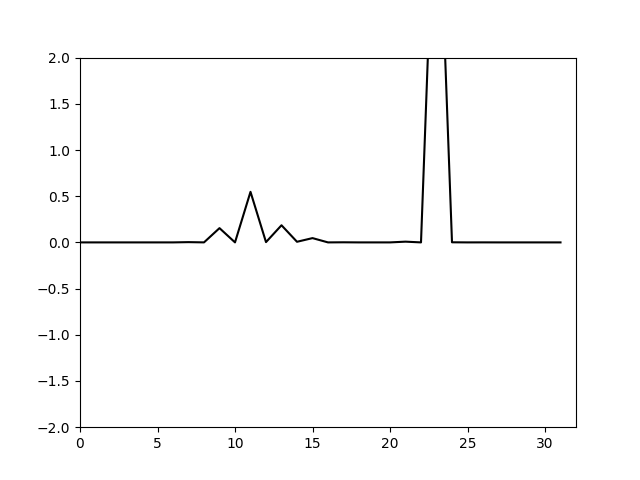
在这里插入图片描述
可以看到这次又出现了奇怪的现象。因为卷积的存在，使得能量会从低波数向高波数传递，而更高的波数被截断了，这部分传递的能量是无法正确计算的。可以看到这个计算即便没有控制能量已经不会像对流方程一样出现网格间的震荡发散。这个计算过程中能力在不同频率的分量间是有转移的，因此不能再用处理对流方程的方法来处理能量增加的问题。这里只能考虑使用一个额外的数值耗散来消耗这部分增加的能量。
空间二阶偏导 $\frac{\partial^2 u}{\partial x^2}$ 项通常称为耗散项，这一项选择合适的系数可以使空间中的能量分布更加均匀，现在方程中添加额外的一个数值耗散。得到新的advance函数

void advance(fftw_complex *us)//单步时间推进
{
	complex<double> *a=(complex<double>*)(us);
    fftw_complex *ts=(fftw_complex*)fftw_malloc(sizeof(fftw_complex)*(N/2+1));
    double *tp=(double*)fftw_malloc(sizeof(double)*N),
    *tp2=(double*)fftw_malloc(sizeof(double)*N);
    for(int i=0;i<N/2+1;i++) 
    {
        *(complex<double>*)(&ts[i])=complex<double>(i*dt*(2*pi/l),0)*complex<double>(0,1)*a[i];
    }
    fft.itran(ts,tp);
    fft.itran(us,tp2);
    for(int i=0;i<N;i++) tp[i]*=tp2[i];
    fft.tran(tp,ts);
    double nu=0.03;
    for(int i=0;i<N/2+1;i++)
	{
		a[i]-=(*(complex<double>*)(&ts[i]))+nu*complex<double>(pow(i*(2*pi/l),2)*dt,0)*a[i];
	}
    fftw_free(ts);
    fftw_free(tp);
    fftw_free(tp2);
}

这里通过调整nu的值可以使得耗散恰好能抑制住推进带来的总能量的增加，通过简单试算大概取到0.03左右即可，计算结果如下。
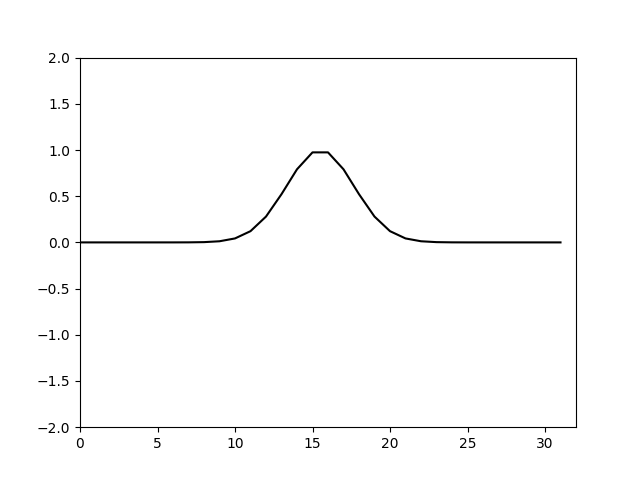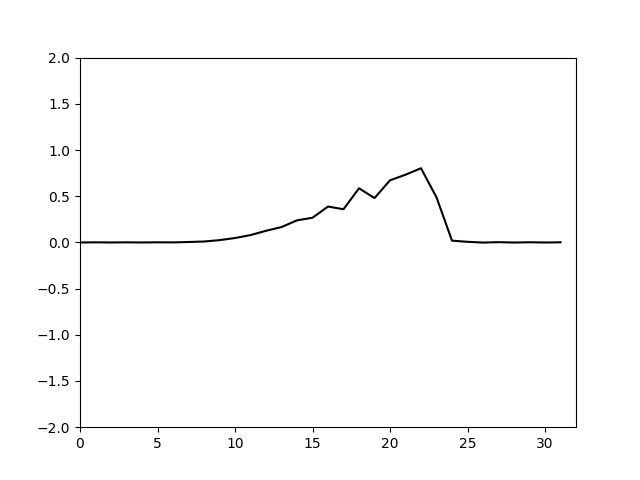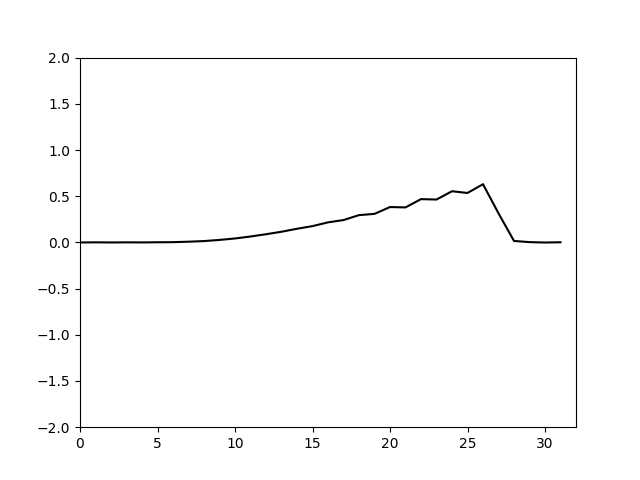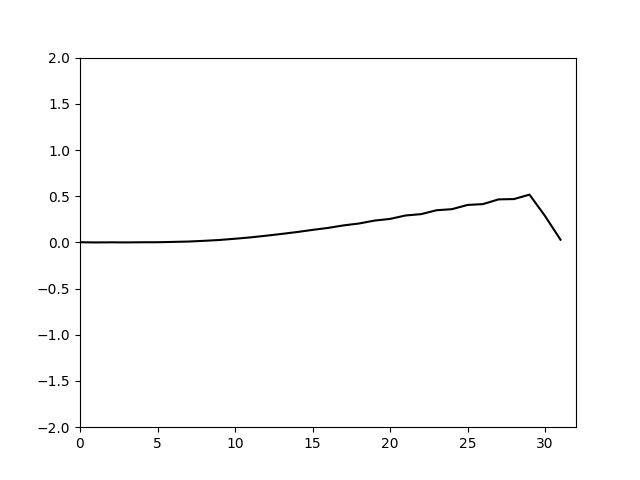
在这里插入图片描述
可以看到计算前期仍有一些高波数分量能体现出来，后期高波数分量基本被抹平，说明耗散基本够了。

接下来我们试着消除前期的高波数分量。首先考察卷积运算中任意两项三角函数的乘积。由积化和差公式
$cos\alpha cos\beta=\frac{1}{2} (cos({\alpha}+{\beta})+cos({\alpha}-{\beta}))$
可以看到任意两个频率的谐波信号的乘积会生成两个不同的谐波分量，当频率都为正时，则会得到一个大于各自频率的分量和一个小于较大频率的分量。如果我们利用傅里叶变换计算卷积时，仅考虑截断频率以下的分量，而不计算卷积中出现的更高频率的分量，这部分高出截断频率的分量同样会影响截断频率以内的谐波分量，这就会产生混淆误差，这是使用谱方法时出现的一种特殊误差。为了消除这部分误差，我们可以在计算卷积时连同更高频率的分量一起计算，而在卷积结果中截断一次，则可以消除这种误差。n阶谱方法的最高频率是 $w_n$ ，卷积后得到的最高频率是 $w_{2n}$ 因此将原序列拓展为2N长的序列来进行卷积即可，拓展的高频分量系数直接设置为0，于是得到了如下的advance函数

void advance(fftw_complex *us)//单步时间推进
{
	complex<double> *a=(complex<double>*)(us);
    fftw_complex *ts=(fftw_complex*)fftw_malloc(sizeof(fftw_complex)*(N+1)),
	*ts2=(fftw_complex*)fftw_malloc(sizeof(fftw_complex)*(N+1));
    double *tp=(double*)fftw_malloc(sizeof(double)*N*2),
    *tp2=(double*)fftw_malloc(sizeof(double)*N*2);
    for(int i=0;i<N+1;i++) 
    {
        if(i<N/2+1) 
		{
			*(complex<double>*)(&ts[i])=complex<double>(i*dt*(2*pi/l),0)*complex<double>(0,1)*a[i];
			*(complex<double>*)(&ts2[i])=a[i];
		}
		else {
			*(complex<double>*)(&ts[i])=complex<double>(0,0);
			*(complex<double>*)(&ts2[i])=complex<double>(0,0);
		}
	}
    fft2.itran(ts,tp);
    fft2.itran(ts2,tp2);
    for(int i=0;i<2*N;i++) tp[i]*=tp2[i];
    fft2.tran(tp,ts);
	double nu=0.02;
    for(int i=0;i<N/2+1;i++)
	{
		a[i]+=(*(complex<double>*)(&ts[i]))-nu*complex<double>(pow(i*(2*pi/l),2)*dt,0)*a[i];
	}
    fftw_free(ts);
    fftw_free(tp);
    fftw_free(tp2);
}

同样试算出nu取0.02。计算结果如下
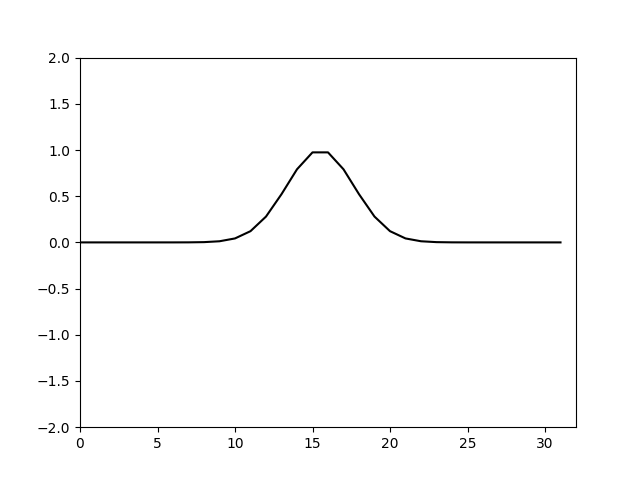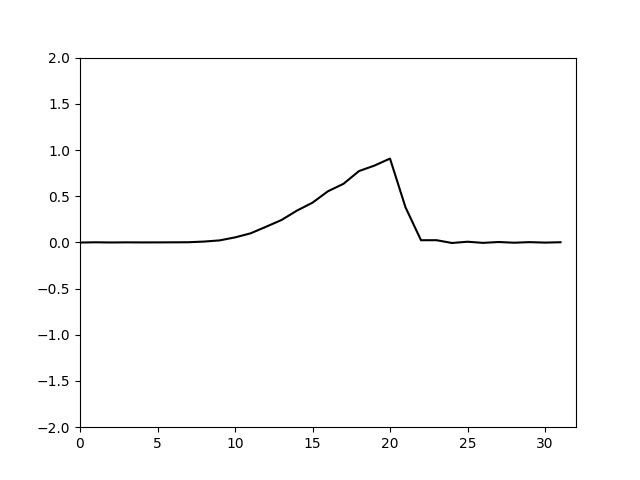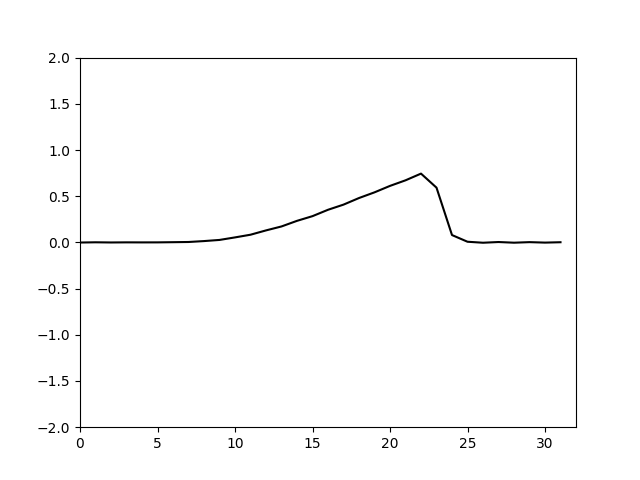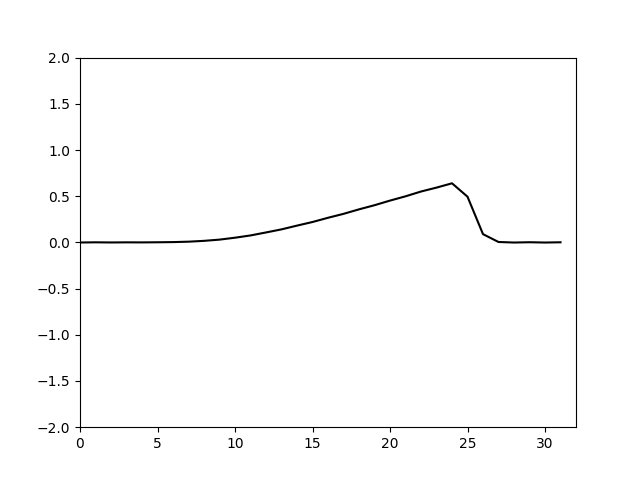
在这里插入图片描述
可以看到消除混淆误差之后，nu取更小的值即可抑制高频震荡，并且在计算初期也不会出现明显的高频谐波分量。根据理论分析的结果，利用傅里叶变换计算卷积，由于截断产生的混淆误差可以通过在计算序列后面补0增加序列长度来消除。实际上当增长的序列长度 $N_2$ 满足 $N_2>N*3/2$ 即可完全消除混淆误差。以这个算例为例，物理空间32个点的序列，要想完全消除混淆误差，需要序列长度至少为49,49-64之间有49、50、54等数都可以利用快速傅里叶变换获得更高的计算效率，而且有可能比64长的序列计算更快，因此可以考虑使用这些长度进行卷积计算。

唯我电磁炮永世长存

发布了22 篇原创文章 · 获赞 9 · 访问量 1万+

私信关注