计算流体力学简介(八)——激波管问题

问题描述

求解如下方程
$u=\left[\begin{matrix} \rho \\ \rho u\\ E \end{matrix}\right], F=\left[\begin{matrix} \rho u\\ \rho u^2+p\\ u(E+p) \end{matrix}\right], E=\frac{p}{\gamma-1}+\frac{1}{2}\rho u^2\\ \ \\ \frac{\partial u}{\partial t}+\frac{\partial F}{\partial x}=0$
的间断初值问题称为激波管问题也叫黎曼问题。
该问题描述的是无粘理想气体在中一根管道中由压力或者速度驱动在突变的初始条件下的变化过程。
通过求解通量的雅各比矩阵 $A=\frac{\partial {\vec F}}{\partial {\vec u}}$可以将前面的控制方程写成
$\frac{\partial u}{\partial t}+A\frac{\partial u}{\partial x}=0$
其中
$u=\left[\begin{matrix} \rho \\ \rho u\\ E \end{matrix}\right], A=\left[\begin{matrix} 0&1&0 \\ -\frac{3-\gamma}{2}u^2&(3-\gamma)u&\gamma-1\\ -u(\frac{1}{\gamma -1}c^2+\frac{2-\gamma}{2}u^2)&\frac{1}{\gamma -1}c^2+\frac{3-2\gamma}{2}u^2&\gamma u \end{matrix}\right]$
其中 $c=\sqrt{\gamma\frac{p}{\rho}}$是声速
对于该方程存在一个特殊关系
以守恒变量表示的守恒形式和非守恒形式的方程之间满足雅各比矩阵 $A$有齐次性
即 $dF=Adu$且 $F=Au$

任何与 $A$相似的矩阵 $B$以及相应的可逆变换 $P$满足 $A=P^{-1}BP$，都可以得到一个新的等价形式
$\frac{\partial (Pu)}{\partial t}+B\frac{\partial (Pu)}{\partial x}=0$
于是根据原变量 $\rho,u,p$可以得到相应的等价形式
$\frac{\partial u}{\partial t}+A\frac{\partial u}{\partial x}=0\\ u=\left[\begin{matrix} \rho \\ u\\ p \end{matrix}\right], A=\left[\begin{matrix} u&\rho&0 \\ 0&u&\frac{1}{\rho}\\ 0&\rho c^2&u \end{matrix}\right]$
通过原变量形式的方程可以很容易计算出矩阵 $A$的特征值，从而得到与 $A$相似的对角阵，将方程解耦，得到三个方程。分别求出三个方程的特征线并对应三个变量，沿三条特征线三个变量的值不发生改变，这三个变量称为黎曼不变量。

问题求解

一根两端封闭的管道内左右两侧有不同的气体，中间以一物体将两侧气体分隔开，左侧气体满足 $\rho_L=1,u_L=0,p_L=1$右侧气体满足 $\rho_L=2,u_L=0,p_L=2$现在突然撤去中间分隔物，两侧气体将在压力作用下相互混合，最终达到平衡状态。
这里以二阶迎风的通量差分格式计算。
由原变量表达的方程中空间导数项的系数矩阵 $A$的特征值为 $u+c,u-c,u$分别表示三个黎曼不变量的传播速度，其中本问题中显然一定有亚音速的区域，因此必然有 $u+c>0,u-c<0$说明方程本身既有向左传播的信息又有向右传播的信息。这时就需要根据信息传播方向决定使用哪一侧的迎风格式。
通量分裂的方法有很多，这里使用Lax-Friedrichs分裂
前面提到了雅各比矩阵的特征值是 $u,u+c,u-c$那么根据当地的 $\rho,u,p$可以很容易计算出三个特征值的值，找到三者中模最大的特征值 $|\lambda|_{max}$然后构造新的雅各比矩阵 $A^+=\frac{A+|\lambda|_{max}I}{2},A^-=\frac{A-|\lambda|_{max}I}{2}$这样必然有 $A=A^++A^-$且 $A^+$的全部特征值大于0， $A^-$的全部特征值小于0，利用守恒型变量雅各比矩阵的齐次性有
$F^+=A^+u=\frac{F+|\lambda|_{max}u}{2},F^-=A^-u=\frac{F-|\lambda|_{max}u}{2}$
于是得到分裂的守恒方程
$\frac{\partial u}{\partial t}+\frac{\partial F^+}{\partial x}+\frac{\partial F^-}{\partial x}=0$
式中第二项表示向右传播的信息，第三项表示向左传播的信息，分别使用 $\frac{3I-4E^{-1}+E^{-2}}{2\Delta x}$和 $-\frac{E^2-4E^1+3I}{2\Delta x}$进行离散。
时间使用单步推进。
具体代码如下

#include <iostream>
#include <vector>
#include <cmath>
#define gamma 1.4
const int NE=100,//空间点数
NS=1000,
SKIP_STEP=10;//时间步数
const double rb=-5,l=10,//计算域左边界，计算域长度
dt=0.005,//时间步长
dx=l/NE;
using namespace std;
void F(vector<double> &_F,double w1,double w2,double w3)
{
    double u=w2/w1,t=u*w2;
    _F[0]=w2;
    _F[1]=(3-gamma)*t/2+(gamma-1)*w3;
    _F[2]=(1-gamma)/2*u*t+gamma*u*w3;
}
void F_div(vector<double>::iterator &f,const vector<double> &F,double w1,double w2,double w3)
{
    *f=F[0];
    f++;
    *f=F[1];
    f++;
    *f=F[2];
    f++;
}
double max(double x1,double x2)
{
    if(x1>x2) return x1;
    else return x2;
}
void advance(vector<double>& w1,vector<double>& w2,vector<double>& w3,vector<double>& F_p,vector<double>& F_m)
{
    vector<double> tF(3,0);
    double l=0;
    vector<double>::iterator f_p=F_p.begin(),f_m=F_m.begin();
    for(int i=0;i<w1.size();i++)
    {
        F(tF,w1[i],w2[i],w3[i]);
        double u=w2[i]/w1[i],p=(gamma-1)*(w3[i]-w2[i]*w2[i]/w1[i]/2),c=sqrt(gamma*p/w1[i]);
        l=max(max(abs(u+c),abs(u-c)),l);
        F_div(f_p,tF,w1[i],w2[i],w3[i]);
        F_div(f_m,tF,w1[i],w2[i],w3[i]);
    }
    for(int i=0;i<w1.size();i++)
    {
        F_p[3*i]+=l*w1[i];
        F_m[3*i]-=l*w1[i]; 
        F_p[3*i+1]+=l*w2[i];
        F_m[3*i+1]-=l*w2[i];  
        F_p[3*i+2]+=l*w3[i];
        F_m[3*i+2]-=l*w3[i]; 
    }
    f_p=F_p.begin()+3,f_m=F_m.begin()+3;
    w1[1]=w1[1]-0.5*(*(f_p)-*(f_p-3))*dt/dx-0.5*(*(f_m+3)-*(f_m))*dt/dx;
    f_p++;
    f_m++;
    w2[1]=w2[1]-0.5*(*(f_p)-*(f_p-3))*dt/dx-0.5*(*(f_m+3)-*(f_m))*dt/dx;
    f_p++;
    f_m++;
    w3[1]=w3[1]-0.5*(*(f_p)-*(f_p-3))*dt/dx-0.5*(*(f_m+3)-*(f_m))*dt/dx;
    f_p++;
    f_m++;
    for(int i=2;i<w1.size()-2;i++)
    {
        
        w1[i]=w1[i]-0.25*(3*(*f_p)-4*(*(f_p-3))+*(f_p-6))*dt/dx
                   +0.25*(*(f_m+6)-4*(*(f_m+3))+3*(*(f_m)))*dt/dx;
        f_p++;
        f_m++;
        w2[i]=w2[i]-0.25*(3*(*f_p)-4*(*(f_p-3))+*(f_p-6))*dt/dx
                   +0.25*(*(f_m+6)-4*(*(f_m+3))+3*(*(f_m)))*dt/dx;
        f_p++;
        f_m++;
        w3[i]=w3[i]-0.25*(3*(*f_p)-4*(*(f_p-3))+*(f_p-6))*dt/dx
                   +0.25*(*(f_m+6)-4*(*(f_m+3))+3*(*(f_m)))*dt/dx;
        f_p++;
        f_m++;
    }
    w1[w1.size()-2]=w1[w1.size()-2]-0.5*(*(f_p)-*(f_p-3))*dt/dx-(*(f_m+3)-*(f_m))*dt/dx;
    f_p++;
    f_m++;
    w2[w2.size()-2]=w2[w2.size()-2]-0.5*(*(f_p)-*(f_p-3))*dt/dx-(*(f_m+3)-*(f_m))*dt/dx;
    f_p++;
    f_m++;
    w3[w3.size()-2]=w3[w3.size()-2]-0.5*(*(f_p)-*(f_p-3))*dt/dx-(*(f_m+3)-*(f_m))*dt/dx;
    f_p++;
    f_m++;
    w1[0]=w1[1];
    w2[0]=-w2[1];
    w3[0]=w3[1];
    w1[w1.size()-1]=w1[w1.size()-2];
    w2[w2.size()-1]=-w2[w2.size()-2];
    w3[w3.size()-1]=w3[w3.size()-2];

}
struct val
{
    const vector<double> &w1,&w2,&w3;
    val(const vector<double>& _w1,const vector<double>& _w2,const vector<double>& _w3):w1(_w1),w2(_w2),w3(_w3){};
};
void init(vector<double> &w1,vector<double> &w2,vector<double> &w3)
{
    int i=1;
    for(;i<w1.size()/2;i++)
    {
        w1[i]=1;
        w2[i]=0;
        w3[i]=2/(gamma-1);
    }
    for(;i<w1.size()-1;i++)
    {
        w1[i]=1;
        w2[i]=0;
        w3[i]=1/(gamma-1);
    }
    w1[0]=w1[1];
    w2[0]=-w2[1];
    w3[0]=w3[1];
    w1[w1.size()-1]=w1[w1.size()-2];
    w2[w2.size()-1]=-w2[w2.size()-2];
    w3[w3.size()-1]=w3[w3.size()-2];
}
ostream& operator<<(ostream& out,const val& Q)
{
    for(int i=1;i<Q.w1.size()-1;i++)
    {
        double rho=Q.w1[i],u=Q.w2[i]/Q.w1[i],p=(gamma-1)*(Q.w3[i]-Q.w2[i]*Q.w2[i]/Q.w1[i]/2);
        out<<i*dx+rb-dx<<'\t'<<rho<<'\t'<<u<<'\t'<<p<<'\n';
    }
    return out;
}
int main()
{
    vector<double> w1(NE+3),w2(NE+3),w3(NE+3),F_p(3*NE+9),F_m(3*NE+9);
    val Q(w1,w2,w3);
    init(w1,w2,w3);
    cout<<w1.size()-2<<'\t'<<NS/SKIP_STEP<<'\t'<<rb<<'\t'<<l<<'\n';
    cout<<Q<<'\n';
    for(int i=0;i<NS;i++)
    {
        advance(w1,w2,w3,F_p,F_m);
        if(i%SKIP_STEP==0)cout<<Q<<'\n';
    }
}

计算结果如下
蓝线是压力，黑线是密度，红线是速度

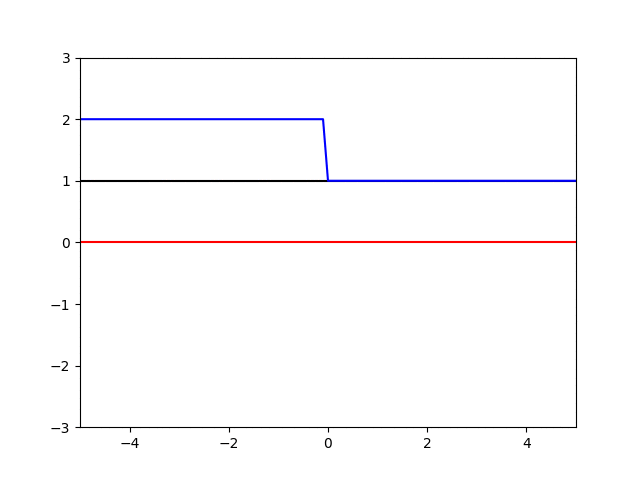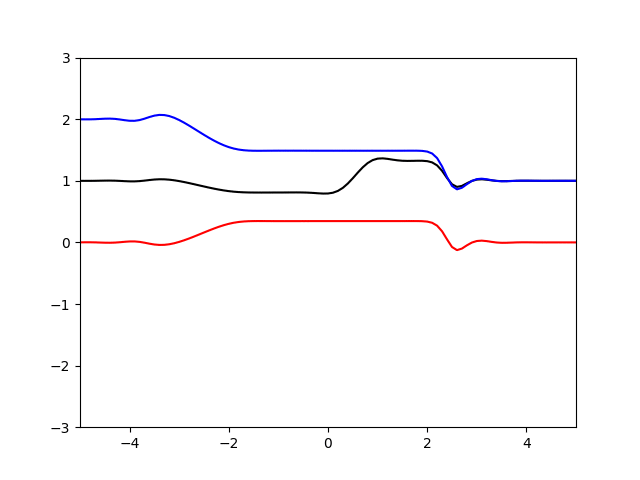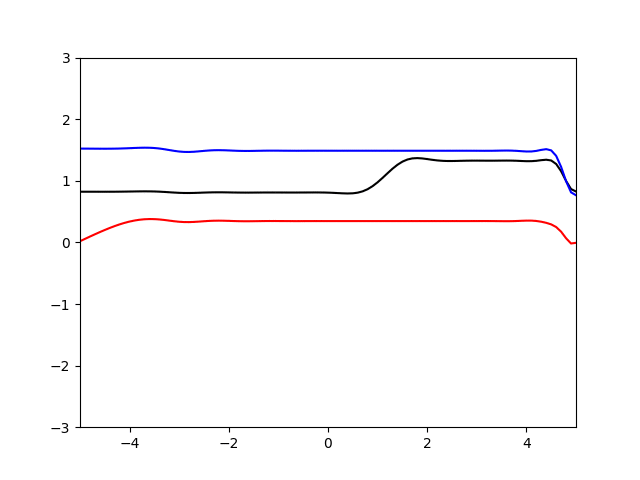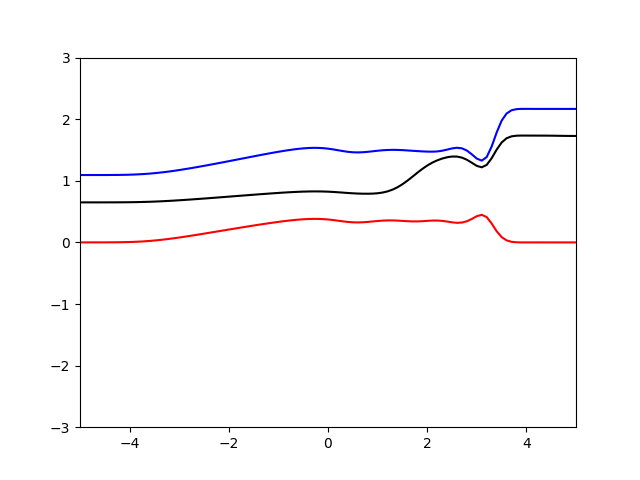
由于我也没有激波管解析解的结果。所以也没办法判断具体结果差多少，不过从网上看到的一些激波管问题的解来看基本规律应该没有太大的问题，不过由于二阶迎风格式的耗散较小，因此间断处有一些震荡。
要想消除震荡可以利用限制器在间断附近使用耗散更大的低阶通量或者使用ENO和WENO格式来抑制震荡。