计算流体力学简介(三)——有限元

有限元原理

以一维模型方程为例
$\frac{\partial u}{\partial t}+\frac{\partial f}{\partial x}=0$
利用变分原理
$\int_L^R(\frac{\partial u}{\partial t}+\frac{\partial f}{\partial x})vdx=0$对于任意 $v$成立。
利用分部积分可以得到
$\int_L^R\frac{\partial u}{\partial t}vdx-\int_L^Rf\frac{\partial v}{\partial x}dx+fv|_R^L=0$
现在由一组基函数 $\varphi_0,\varphi_1,\cdots,\varphi_{n-1}$组成的n维函数空间中求解该变分问题，同时在该空间中取另一组基 $\psi_0,\psi_1,\cdots,\psi_{n-1}$。
$u=\sum u_i\varphi_i，f=\sum f_i\varphi_i，v=\sum v_i\psi_i$则有
$\vec v[\int_L^R\varphi_i\psi_jdx]\vec u'-\vec v[\int_L^R\varphi_i\psi'_jdx]\vec f+f_Rv_R-f_Lv_L=0$
令基函数 $\varphi_i$和 $\psi_i$满足在空间划分的网格单元的单元点 $i$上值为1，其余单元点上均为0。则 $f_Rv_R-f_Lv_L= \vec v \left[\begin{matrix} -1&\cdots&0\\ \vdots&0&\vdots\\ 0&\cdots&1 \end{matrix}\right] \vec f$
设 $A=[\int_L^R\varphi_i\psi_jdx],B=\left[\begin{matrix} -1&\cdots&0\\ \vdots&0&\vdots\\ 0&\cdots&1 \end{matrix}\right]-[\int_L^R\varphi_i\psi'_jdx]$得
$\vec vA\vec u'+\vec vB\vec u=0$对任意 $v\in R^n$成立。因此得
$A\vec u'+B\vec f=0$

一维对流方程

$\frac{\partial u}{\partial t}+c\frac{\partial u}{\partial x}=0$，取 $c=1$，现用有限元法法求解 $\frac{\partial u}{\partial t}+\frac{\partial u}{\partial x}=0$。
初场为 $u_0(x)=e^{-x^2}，x\in[-5,5]$

首先建立网格单元和基函数。
对于任意长度的一维单元都将其先化为 $[0,1]$的标准单元，现使用一阶基函数进行计算，单元点位于单元两侧，即 $(-1,0)、(1,0)$。
$N_0(\xi)=1-\xi\\ N_1(\xi)=\xi$
其中 $\xi=\frac{x-x_i}{h_i}$， $h_i$为单元长度
标准单元和其上的基函数如下图所示

根据标准单元得到标准单元上的系数矩阵 $A，B$

$A=\int_{0}^{1}\left[\begin{matrix} N_0^2&N_0N_1\\ N_0N_1&N_1^2 \end{matrix}\right] d\xi\\ B=\int_0^1\left[\begin{matrix} N_0N_0'&N_0N_1'\\ N_1N_0'&N_1N_1' \end{matrix}\right] \frac{d\xi}{dx}d\xi$
代入 $N_0，N_1$后积分得到
$A=\left[\begin{matrix} \frac{1}{3}&\frac{1}{6}\\ \frac{1}{6}&\frac{1}{3} \end{matrix}\right]\\ B=\frac{1}{h_i}\left[\begin{matrix} -\frac{1}{2}&\frac{1}{2}\\ -\frac{1}{2}&\frac{1}{2} \end{matrix}\right]$
由于各个单元上的基函数都仅在单元内部有值，因此将每个单元上积分得到的方程组扩展到整个计算域只需要在其他位置补零即可。然后将每个单元的方程组叠加组合到一起，即得到整个计算域的离散化方程。利用R-K等方法即可由初值推进求解。
同样按照谱方法的空间步长，将 $[-5,5]$划分为32个等长单元。于是得到
$\left[\begin{matrix} \frac{1}{3}&\frac{1}{6}&0&...&0\\ \frac{1}{6}&\frac{2}{3}&\frac{1}{6}&...&0\\ 0&\frac{1}{6}&\frac{2}{3}&...&0\\ \vdots&&&\ddots\\ 0&0&0&\dots&\frac{1}{3} \end{matrix}\right] \frac{\vec{u}^{n+1}-\vec{u}^n}{\Delta t}- \frac{1}{\Delta x}\left[\begin{matrix} -\frac{1}{2}&\frac{1}{2}&0&...&0\\ -\frac{1}{2}&0&\frac{1}{2}&...&0\\ 0&-\frac{1}{2}&0&...&0\\ \vdots&&&\ddots\\ 0&0&0&\dots&\frac{1}{2} \end{matrix}\right] \vec u^n=0$
简单计算化简一下可以得到
$\vec u^{n+1}=A\vec u^n$的形式，然后即可推进求解。这样可以直接计算，但是由于我希望结果能与伪谱法一样初始波形能一直在计算域内循环，因此需要做一些修改，加上周期边界边界，这个方程本身 $f=u$因此 $f$自然是周期的，我们让 $v$和 $u$满足同样的边界，即 $v$也满足 $v_R=v_L$于是有 $fv|_L^R=0$，因此上面合并出来的 $\vec u^n$一项的系数矩阵并没有再加 $fv|_L^R=0$产生的结果。而为了保证推进时始终有 $u_0=u_{32}$，因此需要将化简后的A矩阵进行修改，由于波形是从左往右传播的，因此将A的第一行改为 $\left[\begin{matrix} 0&0&\cdots&1 \end{matrix}\right]$这只是简单一维问题的一种取巧的方法，对于复杂的方程组问题可能信息会同时向两侧传播，需要进行一些推导使用更为严谨的形式来给出边界条件。
具体代码如下

#include <iostream>
#include <cmath>
#include <vector>
using namespace std;
/************************************************
多项式相关计算，用于生成基函数
************************************************/
struct poly
{
    vector<double> a;
    poly(int n):a(n+1,0){}
    poly(){}
    void set(int n)
    {
        a.resize(n);
        for(int i=0;i<n;i++) a[i]=0;
    }
    const int size()
    {
        return a.size();
    }
    const int size()const
    {
        return a.size();
    }
    double& operator[](int i)
    {
        return a[i];
    }
    const double& operator[](int i)const
    {
        return a[i];
    }
    double operator()(double x)
    {
        double r=0;
        for(int i=a.size()-1;i>0;i--)
        {
            r+=x*a[i];
        }
        return r+a[0];
    }
    poly integ()//不定积分
    {
        poly t;
        t.set(a.size()+1);
        for(int i=1;i<t.size();i++) t[i]=a[i-1]/i;
        return t;
    }
    double integ(double l,double u)//定积分
    {
        poly t;
        t.set(a.size()+1);
        for(int i=1;i<t.size();i++) t[i]=a[i-1]/i;
        return t(u)-t(l);
    }
    poly diff()//导函数
    {
        poly t;
        t.set(a.size()-1);
        for(int i=0;i<t.size();i++) t[i]=a[i+1]*(i+1);
        return t;
    }
    poly diff() const
    {
        poly t;
        t.set(a.size()-1);
        for(int i=0;i<t.size();i++) t[i]=a[i+1]*(i+1);
        return t;
    }
    double diff(double x)//x处导数值
    {
        poly t;
        t.set(a.size()-1);
        for(int i=0;i<t.size();i++) t[i]=a[i+1]*i;
        return t(x);
    }
};
poly operator*(const double k,const poly p)
{
    poly t=p;
    for(int i=0;i<p.size();i++) t[i]=k*p[i];
    return t;
}
poly operator*(const poly p,const double k)
{
    poly t=p;
    for(int i=0;i<p.size();i++) t[i]=k*p[i];
    return t;
}
poly operator/(const double k,const poly p)
{
    poly t=p;
    for(int i=0;i<p.size();i++) t[i]=k/p[i];
    return t;
}
poly operator/(const poly p,const double k)
{
    poly t=p;
    for(int i=0;i<p.size();i++) t[i]=k/p[i];
    return t;
}
poly operator*(const poly p1,const poly p2)
{
    poly t;
    t.set(p1.size()+p2.size()-1);
    for(int i=0;i<p1.size();i++)
    {
        for(int j=0;j<p2.size();j++) t[i+j]+=p1[i]*p2[j];
    }
    int i=t.size(),j=i-1;
    for(;j>=0;j--)
    {
        if(t[j]!=0) break;
    }
    t.a.resize(j+1);
    return t;
}
ostream& operator<<(ostream& out,const poly p)
{
    for(int i=p.size()-1;i>0;i--) out<<p[i]<<'\t';
    out<<p[0];
    return out;
}
vector<poly> creat_base(int n)//生成拉格朗日插值基函数
{
    vector<poly> r(n+1,poly(0));
    for(int i=0;i<n+1;i++)
    {
        r[i][0]=1;
        for(int j=0;j<n+1;j++)
        {
            if(j==i) continue;
            poly t(1);
            t[0]=-j/(i-j);
            t[1]=n/(i-j);
            r[i]=r[i]*t;
        }
    }
    return r;
}
/************************************************
矩阵相关计算
************************************************/
struct matrix
{
    vector<vector<double>> a;
    matrix(){}
    matrix(int r,int c):a(r,vector<double>(c,0)){}
    void set(int r,int c)
    {
        a.resize(r);
        for(int i=0;i<r;i++) 
        {
            a[i].resize(c);
            for(int j=0;j<c;j++) a[i][j]=0;
        }
    }
    vector<double>& operator[](int i)
    {
        return a[i];
    }
    const vector<double>& operator[](int i)const
    {
        return a[i];
    }
    const int row()
    {
        return a.size();
    }
    const int col()
    {
        if(a.size()==0) return 0;
        return a[0].size();
    }
    const int row() const
    {
        return a.size();
    }
    const int col() const
    {
        if(a.size()==0) return 0;
        return a[0].size();
    }
    matrix operator-()
    {
        matrix A(row(),col());
        for(int i=0;i<row();i++)
        {
            for(int j=0;j<col();j++)
            {
                A[i][j]=-a[i][j];
            }
        }
        return A;
    }
};
matrix operator+(const matrix& A,const matrix& B)
{
    if(A.row()!=B.row()||A.col()!=B.col())
    {
        cout<<"matrix operator+:维度不匹配"<<endl;
        return matrix();
    }
    matrix C(A.row(),A.col());
    for(int i=0;i<C.row();i++)
    {
        for(int j=0;j<C.col();j++)
        {
            C[i][j]=A[i][j]+B[i][j];
        }
    }
    return C;
}
matrix operator-(const matrix& A,const matrix& B)
{
    if(A.row()!=B.row()||A.col()!=B.col())
    {
        cout<<"matrix operator+:维度不匹配"<<endl;
        return matrix();
    }
    matrix C(A.row(),A.col());
    for(int i=0;i<C.row();i++)
    {
        for(int j=0;j<C.col();j++)
        {
            C[i][j]=A[i][j]-B[i][j];
        }
    }
    return C;
}
matrix operator*(const double k,const matrix& A)
{
    matrix C(A.row(),A.col());
    for(int i=0;i<C.row();i++)
    {
        for(int j=0;j<C.col();j++)
        {
            C[i][j]=A[i][j]*k;
        }
    }
    return C;
}
vector<double> operator*(const matrix& A,const vector<double>& x)
{
    if(A.row()!=x.size())
    {
        cout<<"operator *:维度不匹配"<<endl;
        return vector<double>();
    }
    vector<double> r(x.size(),0);
    for(int i=0;i<A.row();i++)
    {
        for(int j=0;j<A.col();j++)
        {
            r[i]+=A[i][j]*x[j];
        }
    }
    return r;
}
matrix operator*(const matrix& A,const double k)
{
    matrix C(A.row(),A.col());
    for(int i=0;i<C.row();i++)
    {
        for(int j=0;j<C.col();j++)
        {
            C[i][j]=A[i][j]*k;
        }
    }
    return C;
}
matrix operator/(const matrix& A,const double k)
{
    matrix C(A.row(),A.col());
    for(int i=0;i<C.row();i++)
    {
        for(int j=0;j<C.col();j++)
        {
            C[i][j]=A[i][j]/k;
        }
    }
    return C;
}
ostream& operator<<(ostream& out,const matrix& A)
{
    for(int i=0;i<A.row();i++)
    {
        for(int j=0;j<A.col()-1;j++)
        {
            out<<A[i][j]<<'\t';
        }
        out<<A[i][A.col()-1]<<'\n';
    }
    return out;
}
/************************************************
矢量和矩阵相关计算
************************************************/
ostream& operator<<(ostream& out,const vector<double>& A)
{
        for(int j=0;j<A.size()-1;j++)
        {
            out<<A[j]<<'\t';
        }
        out<<A[A.size()-1];
    return out;
}
double norm(const vector<double>& x)//二范数、模
{
    double r=0;
    for(int i=0;i<x.size();i++) r+=x[i]*x[i];
    return sqrt(r);
}
vector<double>& operator/(vector<double>& A,const double k)
{
    for(int i=0;i<A.size();i++)
    {
        A[i]=A[i]/k;
    }
    return A;
}
double operator*(const vector<double>& a,const vector<double>& b)
{
    if(a.size()!=b.size())
    {
        cout<<"点积维度不匹配"<<endl;
        return 0;
    }
    double r=0;
    for(int i=0;i<a.size();i++) r+=a[i]*b[i];
    return r;
}
double power_method(const matrix& A)//幂法求谱半径
{
    vector<double> t(A.row(),1),t0(t);
    double beta=0,beta0=1;
    while(abs(beta-beta0)>1e-7)
    {
        beta0=beta;
        t=t/norm(t);
        t0=t;
        t=A*t;
        beta=t0*t;
    }
    return beta;
}
void op1(matrix& A,int i,int j)
{
    for(int k=0;k<A[0].size();k++)
    {
        swap(A[i][k],A[j][k]);
    }
}
void op2(matrix& A,int i,double k)
{
    for(int j=0;j<A[0].size();j++)
    {
        A[i][j]*=k;
    }
}
void op3(matrix& A,int i,int j,double k)
{
    for(int l=0;l<A[0].size();l++)
    {
        A[j][l]+=k*A[i][l];
    }
}
int maxr(const matrix &A,int j)
{
    int Mr=j;
    double M=A[j][j];
    for(int i=j+1;i<A.a.size();i++)
    {
        if(abs(A[i][j])>M)
        {
            M=abs(A[i][j]);
            Mr=i;
        }
    }
    return Mr;
}
void inv_mul(matrix A,matrix& B)//inv(A)*B
{
    int rank=A.a.size();
    for(int i=0;i<A.a.size();i++)
    {
        int m=maxr(A,i);
        op1(A,i,m);
        op1(B,i,m);
        op2(B,i,1/A[i][i]);
        op2(A,i,1/A[i][i]);
        for(int j=i+1;j<A.a.size();j++)
        {
            op3(B,i,j,-A[j][i]);
            op3(A,i,j,-A[j][i]);
        }
    }
    for(int i=A.a.size()-1;i>=0;i--)
    {
        for(int k=i-1;k>=0;k--)
        {
            op3(B,i,k,-A[k][i]);
        } 
    }
}

matrix creat_At(int n,const vector<poly>& N)//获得时间项在标准单元上的系数矩阵
{
    if(N.size()!=n+1)
    {
        cout<<"creat_At:阶数不匹配"<<endl;
        return matrix();
    }
    matrix _At(n+1,n+1);
    for(int i=0;i<n+1;i++)
    {
        for(int j=0;j<n+1;j++)
        {
            _At[i][j]=(N[i]*N[j]).integ(0,1);
        }
    }
    return _At;
}
matrix creat_Ax(int n,const vector<poly>& N)//获得一阶空间导数项在标准单元上的系数矩阵
{
    if(N.size()!=n+1)
    {
        cout<<"creat_Ax:阶数不匹配"<<endl;
        return matrix();
    }
    matrix _Ax(n+1,n+1);
    for(int i=0;i<n+1;i++)
    {
        for(int j=0;j<n+1;j++)
        {
            poly t=N[j].diff();
            _Ax[i][j]=-(N[i]*t).integ(0,1);
        }
    }
    return _Ax;
}
matrix creat_Axx(int n,const vector<poly>& N)//获得二阶空间导数项在标准单元上的系数矩阵
{
    if(N.size()!=n+1)
    {
        cout<<"creat_Ax:阶数不匹配"<<endl;
        return matrix();
    }
    matrix _Ax(n+1,n+1);
    for(int i=0;i<n+1;i++)
    {
        for(int j=0;j<n+1;j++)
        {
            poly t1=N[i].diff(),t2=N[j].diff();
            _Ax[i][j]=(t1*t2).integ(0,1);
        }
    }
    return _Ax;
}
matrix get_A(int n,int o,const matrix& _A)//合并所有单元(该函数要求所有单元长度相等，如果不等需要额外修改合并方式)
{
    matrix A(o*n+1,o*n+1);
    for(int i=0;i<n;i++)
    {
        for(int j=0;j<o+1;j++)
        {
            for(int k=0;k<o+1;k++)
            {
                A[i*o+j][i*o+k]+=_A[j][k];
            }
        }
    }
    return A;
}
const int order=1;
const int NE=32,//空间单元数
NS=100;//时间步数
const double rb=-5,l=10,//计算域左边界，计算域长度
dt=0.1,//时间步长
dx=l/NE;
void init_guass(vector<double> &u0)//设置高斯函数初场
{
    for(int i=0;i<u0.size();i++) 
	{
		u0[i]=exp(-pow((l*double(i)/(NE-1)+rb),2));
	}
}
int main()
{
     vector<double> u0(NE+1);
    init_guass(u0);
    vector<poly> N=creat_base(order);
    matrix _At=creat_At(order,N),_Ax=creat_Ax(order,N),
    At=get_A(NE,order,_At),Ax=get_A(NE,order,_Ax),A(NE+1,NE+1);
    A=At+Ax*(dt/dx);
    inv_mul(At,A);
    A[0][A.col()-1]=1;
    for(int i=0;i<A.col()-1;i++) A[0][i]=0;
    cout<<NE+1<<'\t'<<NS<<'\t'<<rb<<'\t'<<l<<'\n';
    cout<<u0<<'\n';
    for(int i=0;i<NS;i++)
    {
        u0=A*u0;
        cout<<u0<<'\n';
    }
    retrun 0;
}

计算结果如下

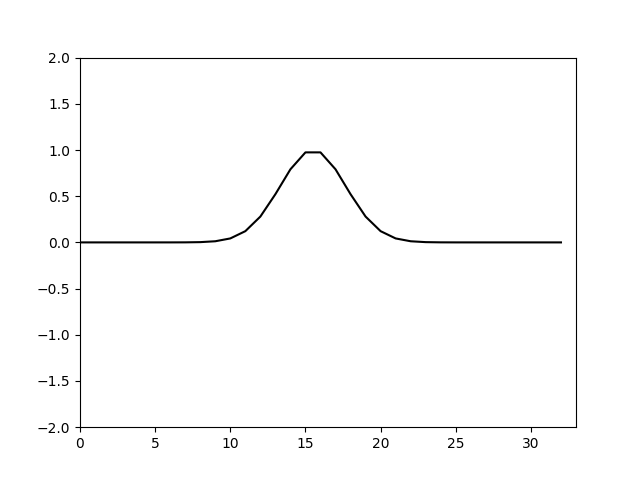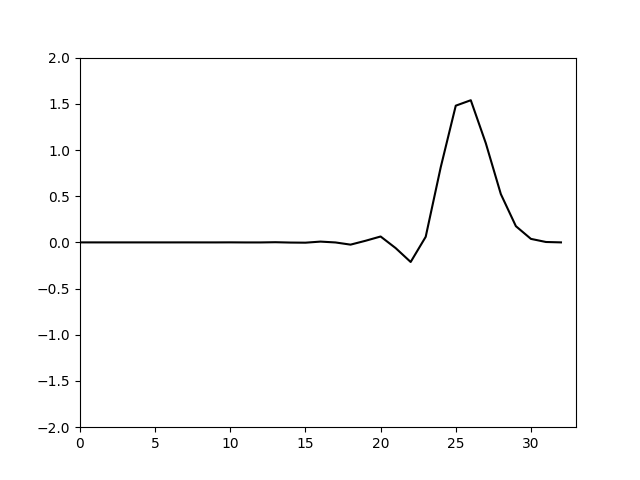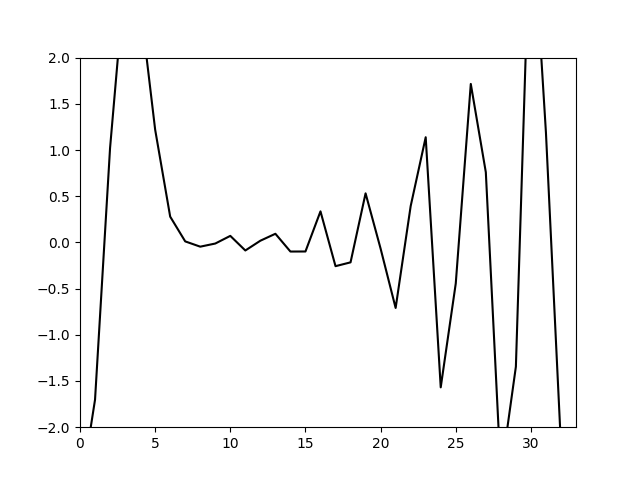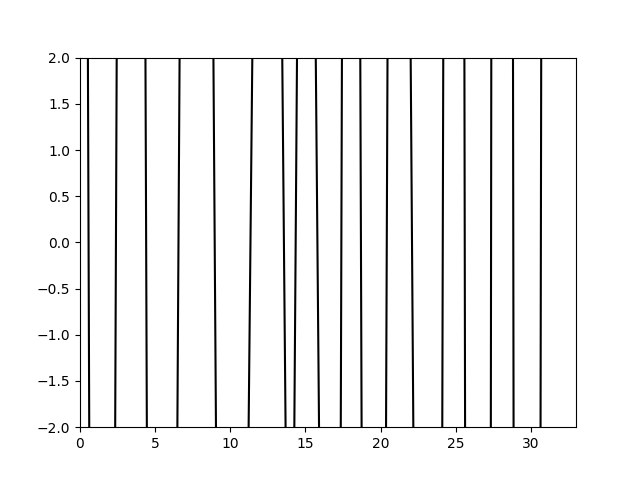
可以看到计算仍然不稳定，因此与伪谱法相同，同样使用人工粘性，在方程右端额外添加一个二阶导数项进行求解。添加一个求空间二阶导数项系数矩阵的函数并合并到之前计算出的 $A$中

matrix creat_Axx(int n,const vector<poly>& N)//获得二阶空间导数项在标准单元上的系数矩阵
{
    if(N.size()!=n+1)
    {
        cout<<"creat_Ax:阶数不匹配"<<endl;
        return matrix();
    }
    matrix _Ax(n+1,n+1);
    for(int i=0;i<n+1;i++)
    {
        for(int j=0;j<n+1;j++)
        {
            poly t1=N[i].diff(),t2=N[j].diff();
            _Ax[i][j]=(t1*t2).integ(0,1);
        }
    }
    return _Ax;
}
int main()
{
    vector<double> u0(NE+1);
    init_guass(u0);
    vector<poly> N=creat_base(order);
    matrix _At=creat_At(order,N),_Ax=creat_Ax(order,N),_Axx=creat_Axx(order,N),
    At=get_A(NE,order,_At),Ax=get_A(NE,order,_Ax),Axx=get_A(NE,order,_Axx),A(NE+1,NE+1);
    double nu=0.5;
    A=At+Ax*(dt/dx)-nu*Axx*(dt/dx*dx);
    inv_mul(At,A);
    A[NE][0]=1;
    for(int i=1;i<A.col();i++) A[NE][i]=0;
    cout<<NE+1<<'\t'<<NS<<'\t'<<rb<<'\t'<<l<<'\n';
    cout<<u0<<'\n';
    for(int i=0;i<NS;i++)
    {
        u0=A*u0;
        cout<<u0<<'\n';
    }
    return 0;
}

试算出 $\nu=0.5$计算结果如下

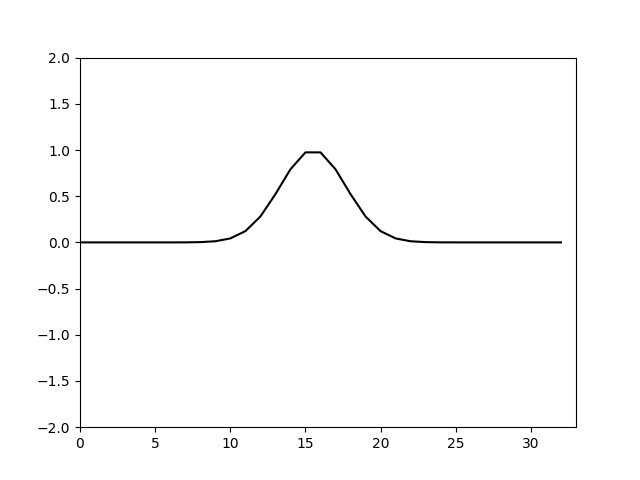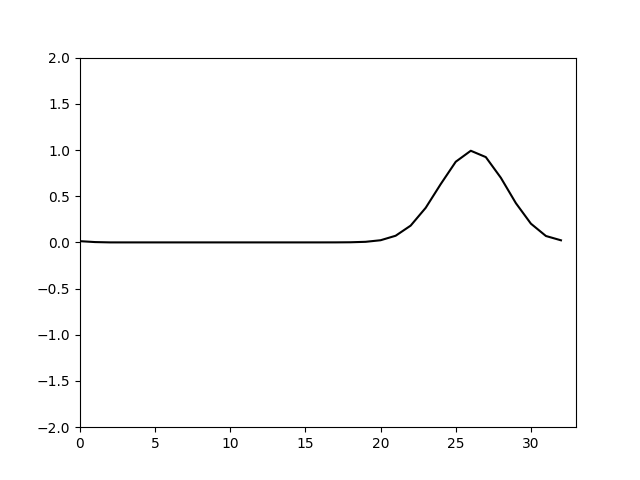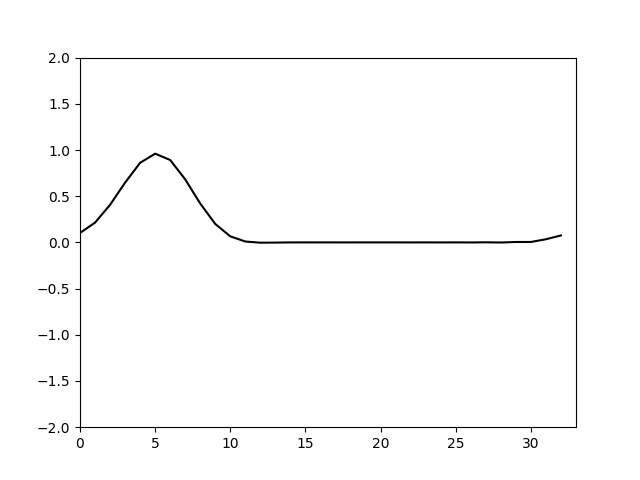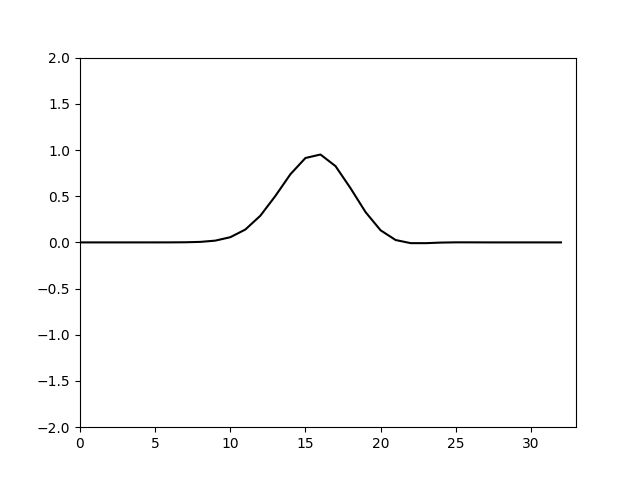
可以看到加上合适的人工粘性后计算就收敛了。

无粘Burgers方程

现用有限元法法求解 $\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}=0$。
初场为 $u_0(x)=e^{-x^2}，x\in[-5,5]$，同样取周期边界。
同样使用一阶拉格朗日插值单元
$\left[\begin{matrix} \frac{1}{3}&\frac{1}{6}&0&...&0\\ \frac{1}{6}&\frac{2}{3}&\frac{1}{6}&...&0\\ 0&\frac{1}{6}&\frac{2}{3}&...&0\\ \vdots&&&\ddots\\ 0&0&0&\dots&\frac{1}{3} \end{matrix}\right] \frac{\vec{u}^{n+1}-\vec{u}^n}{\Delta t}- \frac{1}{\Delta x}\left[\begin{matrix} -\frac{1}{2}&\frac{1}{2}&0&...&0\\ -\frac{1}{2}&0&\frac{1}{2}&...&0\\ 0&-\frac{1}{2}&0&...&0\\ \vdots&&&\ddots\\ 0&0&0&\dots&\frac{1}{2} \end{matrix}\right] \vec {(u^2)}^n=0$
只需要在前面代码的基础上再添加一个计算 $u^2$的函数，并修改主函数即可

vector<double> sq(const vector<double>& x)//每个分量都平方
{
    vector<double> r(x.size());
    for(int i=0;i<x.size();i++)r[i]=x[i]*x[i];
    return r;
}
int main()
{
    vector<double> u0(NE+1);
    init_guass(u0);
    vector<poly> N=creat_base(order);
    matrix _At=creat_At(order,N),_Ax=creat_Ax(order,N),_Axx=creat_Axx(order,N),
    At=get_A(NE,order,_At),Ax=get_A(NE,order,_Ax),Axx=get_A(NE,order,_Axx),A(NE+1,NE+1),inv_At(NE+1,NE+1);
    for(int i=0;i<NE+1;i++) inv_At[i][i]=1;
    inv_mul(At,inv_At);
    double nu=0.5;
    
    cout<<NE+1<<'\t'<<NS<<'\t'<<rb<<'\t'<<l<<'\n';
    cout<<u0<<'\n';
    for(int i=0;i<NS;i++)
    {
        u0=At*u0+(0.5*dt/dx)*Ax*sq(u0)-nu*Axx*(dt/dx*dx)*u0;
        u0=inv_At*u0;
        u0[0]=u0[NE];
        cout<<u0<<'\n';
    }
    return 0;
}

取 $\nu=0.5$计算结果如下

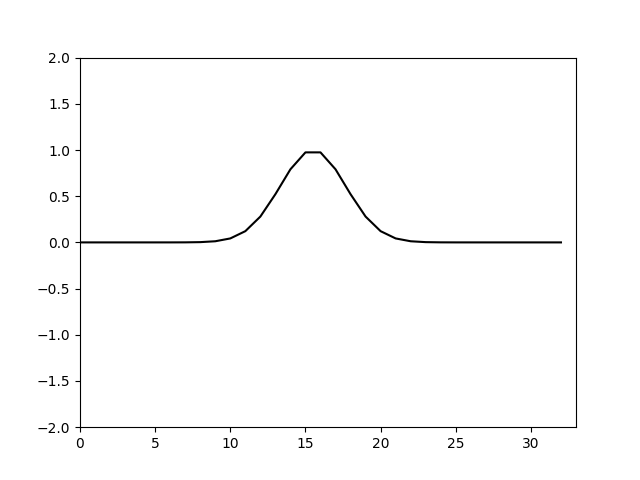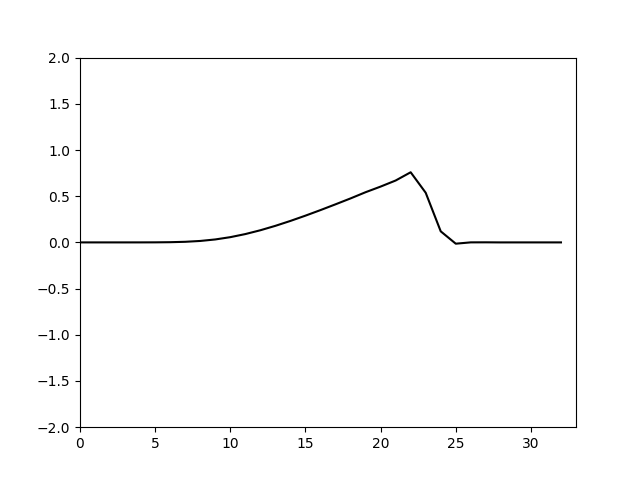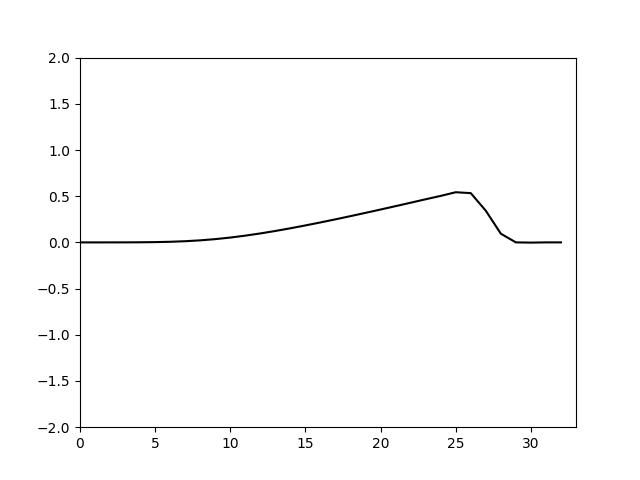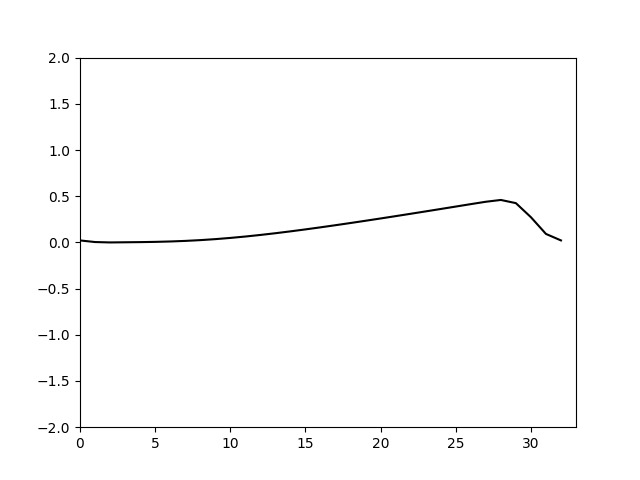
可以看到结果和伪谱法的到基本相同。

一些其它问题

这是我第一次用有限元求解带一阶空间偏导的偏微分方程，以前只用有限元解过抛物型的传热方程，没想到两个方程的求解异常顺利。因为对流方程由于信息的传递是有方向的，通常需要一些迎风的处理，而Burgers方程的非线性带来的数值上的间断，通常的数值方法很容易在间断处产生异常震荡，导致计算发散，因此也需要限制器等方式抑制间断处的震荡。之前看到的有限元解决这两个问题是使用的迎风有限元和间断有限元。

迎风有限元是在基函数上添加一个不影响单元点值的迎风的函数 $F(\xi),F(0)=F(1)=0$作为权函数( $\psi_i$)使得单元内上的权函数具有迎风性质，从而保证信息传播的方向性，使格式稳定，没想到直接加人工粘性就可稳定，不过这个人工粘性系数是一个可变参数需要调节，如果这个人工粘性项系数标定不准确则成为一个二阶误差进入方程当中，不像迎风有限元一样直接给出高阶的基函数构造即可保证空间精度。不过可以利用一些稳定性分析手段将其用 $\Delta x、\Delta t$的函数来近似，从而避免额外的参数调节。

间断有限元是专门处理激波处异常数值震荡的方法。这个方法和通量重构有些类似，即通量 $f$的单元和守恒量 $u$的单元错开了半个网格，从而保证数值格式的守恒律，再通过添加限制器加强激波附近的耗散，抑制异常的数值震荡。

不过没想到Burgers方程也直接利用普通的人工粘性就可以抑制间断附近的震荡，甚至连人工粘性的耗散系数都不用调整，结果也精度也还可以。