【R参数估计】区间估计

估计量的优良性准则

无偏性

估计量是随机变量，对于不同的样本值就会得到不同的估计值，这样，要确定一个估计量的好坏，就必须由多次抽样结果决定。对此，一个自然而基本的衡量标准是要求估计量无系统偏差，即在大量重复抽样（样本容量相同）时，所得的估计值平均起来应与待估参数的真值相同，这就是所谓的无偏性要求。

有效性

在许多情况下，总体参数Θ的无偏估计量不是唯一的，要衡量一个参数的两个无偏估计量哪一个更好，一个重要的标准就是观察它们谁的取值更集中于待估参数的真值附近，即哪一个估计量的方差更小，这就是所谓的有效性要求。

相合性（一致性）

一个好的估计量，当样本容量n越大时，由于关于总体的信息也随之增加，该估计理应越精确越可靠，特别是当n→∞时，估计值将与参数真值几乎完全一致，这就是估计量的相合性（一致性）。

区间估计（interval estimation）

对于前文提到的点估计方法，我们无法回答它的精确性如何？可信程度如何？为了解决这些问题，需要讨论参数的区间估计。

区间估计是用两个统计量所构成的区间来估计一个未知的参数，并同时指明此区间可以覆盖住这个参数的可靠程度（置信度）
缺点：不能直接地告诉人们“未知参数具体是多少”这一明确的概念

一个正态总体的情况

均值μ的方差估计

总体方差已知和方差未知两种情况均值μ区间估计的R程序：

interval_estimate1<-function(x,sigma=-1,alpha=0.05){ 
   n<-length(x); xb<-mean(x)
   if (sigma>=0){
      tmp<-sigma/sqrt(n)*qnorm(1-alpha/2); df<-n
   }
   else{
      tmp<-sd(x)/sqrt(n)*qt(1-alpha/2,n-1); df<-n-1
   }
   data.frame(mean=xb, df=df, a=xb-tmp, b=xb+tmp)
}

得到观测数据后，利用此函数对参数μ作区间估计：

source("interval_estimate1.R")
X<-c(14.6, 15.1,14.9, 14.8, 15.2,15.1)
interval_estimate1(X, sigma=0.2)

得到的结果如下

故该组观测数据的置信系数为0.95的置信区间为[14.79,15.11]

R软件中的t.test检验函数可以完成相应的区间估计工作

t.test(X)

结果如下：

方差σ²的区间估计

总体均值已知和均值未知两种情况方差σ²区间估计的R程序：

interval_var1<-function(x,mu=Inf,alpha=0.05){ 
   n<-length(x) 
   if (mu<Inf){
      S2 <- sum((x-mu)^2)/n; df <- n
   }
   else{
      S2 <- var(x); df <- n-1
   }
   a<-df*S2/qchisq(1-alpha/2,df)
   b<-df*S2/qchisq(alpha/2,df)
   data.frame(var=S2, df=df, a=a, b=b)
}

输入数据，调用程序

source("interval_var1.R")
X<-c(10.1,10,9.8,10.5,9.7,10.1,9.9,10.2,10.3,9.9)
interval_var1(X,mu=10)

得到结果如下

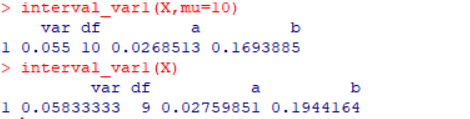
从计算结果可以看出，在均值已知的情况下，计算结果更好一些

两个正态总体的情况

均值差μ1-μ2的区间估计

均值差μ1-μ2区间估计的R程序：

interval_estimate2<-function(x, y, 
   sigma=c(-1,-1),var.equal=FALSE, alpha=0.05){ 
   n1<-length(x); n2<-length(y)
   xb<-mean(x); yb<-mean(y)
   if (all(sigma>=0)){
      tmp<-qnorm(1-alpha/2)*sqrt(sigma[1]^2/n1+sigma[2]^2/n2)
      df<-n1+n2
   }
   else{
      if (var.equal ==  TRUE){
         Sw<-((n1-1)*var(x)+(n2-1)*var(y))/(n1+n2-2)
         tmp<-sqrt(Sw*(1/n1+1/n2))*qt(1-alpha/2,n1+n2-2)
         df<-n1+n2-2
      }
      else{
         S1<-var(x); S2<-var(y)
         nu<-(S1/n1+S2/n2)^2/(S1^2/n1^2/(n1-1)+S2^2/n2^2/(n2-1))
         tmp<-qt(1-alpha/2, nu)*sqrt(S1/n1+S2/n2)
         df<-nu
      }
   }
   data.frame(mean=xb-yb, df=df, a=xb-yb-tmp, b=xb-yb+tmp)
}

首先产生200个随机数，再调用函数interval_estimate2()进行计算

source("interval_estimate2.R")
x<-rnorm(100, 5.32, 2.18)
y<-rnorm(100, 5.76, 1.76)
interval_estimate2(x,y, sigma=c(2.18,1.76))

得到结果如下：

故μ1-μ2的置信系数为0.95的区间估计为[-1.044,0.546]

R软件中的t.test()函数也可以给出双样本差的区间估计

t.test(x,y)

得到的结果如下：

配对数据的区间估计

例如：

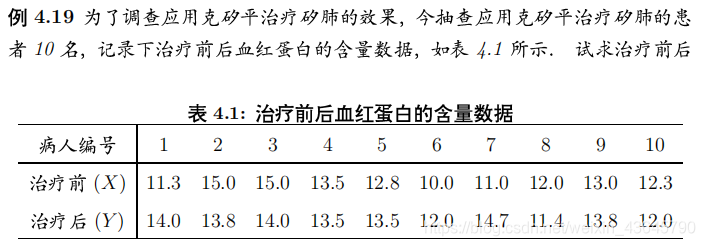
输入数据，调入t.test()函数

X<-c(11.3,15.0,15.0,13.5,12.8,10.0,11.0,12.0,13.0,12.3)
Y<-c(14.0,13.8,14.0,13.5,13.5,12.0,14.7,11.4,13.8,12.0)
t.test(X-Y)

得到的结果如下：

由于0包含在区间估计的区间内，因此可以认为：治疗前后病人的血红蛋白的含量无明显差异。

方差比σ1²/σ2²的区间估计

方差比σ1²/σ2²区间估计的R程序：

interval_var2<-function(x,y, 
   mu=c(Inf, Inf), alpha=0.05){ 
   n1<-length(x); n2<-length(y) 
   if (all(mu<Inf)){
      Sx2<-1/n1*sum((x-mu[1])^2); Sy2<-1/n2*sum((y-mu[2])^2)
      df1<-n1; df2<-n2
   }
   else{
      Sx2<-var(x); Sy2<-var(y); df1<-n1-1; df2<-n2-1
   }
   r<-Sx2/Sy2
   a<-r/qf(1-alpha/2,df1,df2)
   b<-r/qf(alpha/2,df1,df2)
   data.frame(rate=r, df1=df1, df2=df2, a=a, b=b)
}

输入数据，调用函数

A<-scan()
79.98 80.04 80.02 80.04 80.03 80.03 80.04 79.97
80.05 80.03 80.02 80.00 80.02

B<-scan()
80.02 79.94 79.98 79.97 79.97 80.03 79.95 79.97

source("interval_var2.R")
interval_var2(A,B, mu=c(80,80)) #均值已知

interval_var2(A,B) #均值未知

var.test(A,B)

得到的结果如下：

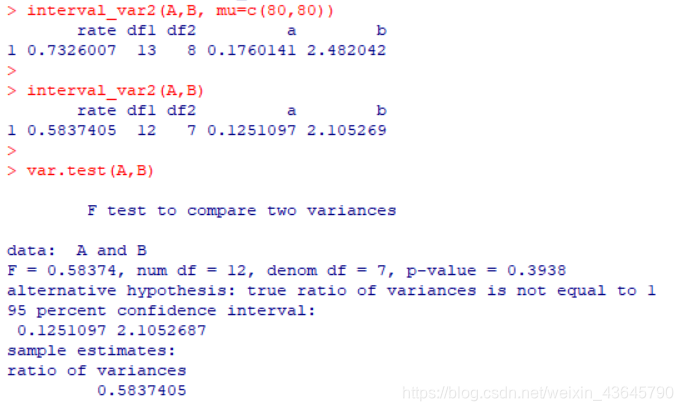
1包含在区间估计的区间中，即有理由认为两总体的方差比为1，即可认为两总体的方差是相同的。

非正态总体的区间估计

当数据不服从正态分布时，估计均值的一种有效的方法就是所谓的大样本方法，即要求样本的量比较大，利用中心极限定理进行分析。
非正态总体区间估计的R程序：

interval_estimate3<-function(x,sigma=-1,alpha=0.05){ 
   n<-length(x); xb<-mean(x)
   if (sigma>=0)
      tmp<-sigma/sqrt(n)*qnorm(1-alpha/2)
   else
      tmp<-sd(x)/sqrt(n)*qnorm(1-alpha/2)
   data.frame(mean=xb, a=xb-tmp, b=xb+tmp)
}

例如：

先产生随机数，再调用函数

source("interval_estimate3.R")
> x<-rexp(50,1/2.266)
> interval_estimate3(x)

得到结果如下：

单侧置信区间估计

对于某些问题，人们只关心在某一方向上的界限，这类区间估计问题就被称为单侧区间估计。

一个总体求均值

根据计算公式及双侧置信区间的公式写出R程序，并可控制求上、下置信区间或双侧置信区间。

interval_estimate4<-function(x, sigma=-1, side=0, alpha=0.05){ 
   n<-length(x); xb<-mean(x)
   if (sigma>=0){
      if (side<0){
         tmp<-sigma/sqrt(n)*qnorm(1-alpha)
         a <- -Inf; b <- xb+tmp
      }
      else if (side>0){
         tmp<-sigma/sqrt(n)*qnorm(1-alpha)
         a <- xb-tmp; b <- Inf
      }
      else{
         tmp <- sigma/sqrt(n)*qnorm(1-alpha/2)
         a <- xb-tmp; b <- xb+tmp
      }
      df<-n
   }
   else{
      if (side<0){
         tmp <- sd(x)/sqrt(n)*qt(1-alpha,n-1)
         a <- -Inf; b <- xb+tmp
      }
      else if (side>0){
         tmp <- sd(x)/sqrt(n)*qt(1-alpha,n-1)
         a <- xb-tmp; b <- Inf
      }
      else{
         tmp <- sd(x)/sqrt(n)*qt(1-alpha/2,n-1)
         a <- xb-tmp; b <- xb+tmp
      }
      df<-n-1
   }
   data.frame(mean=xb, df=df, a=a, b=b)
}

一个总体求方差

interval_var3<-function(x,mu=Inf,side=0,alpha=0.05){ 
   n<-length(x)
   if (mu<Inf){
      S2<-sum((x-mu)^2)/n; df<-n
   }
   else{
      S2<-var(x); df<-n-1
   }
   if (side<0){
      a <- 0
      b <- df*S2/qchisq(alpha,df)
   }
   else if (side>0){
      a <- df*S2/qchisq(1-alpha,df)
      b <- Inf
   }
   else{
      a<-df*S2/qchisq(1-alpha/2,df)
      b<-df*S2/qchisq(alpha/2,df)
   }
   data.frame(var=S2, df=df, a=a, b=b)
}

两个总体求均值差

interval_estimate5<-function(x, y, 
   sigma=c(-1,-1), var.equal=FALSE, side=0, alpha=0.05){ 
   n1<-length(x); n2<-length(y)
   xb<-mean(x); yb<-mean(y); zb<-xb-yb
   if (all(sigma>=0)){
      if (side<0){
         tmp<-qnorm(1-alpha)*sqrt(sigma[1]^2/n1+sigma[2]^2/n2)
         a <- -Inf; b <- zb+tmp
      }
      else if (side>0){
         tmp<-qnorm(1-alpha)*sqrt(sigma[1]^2/n1+sigma[2]^2/n2)
         a <- zb-tmp; b <- Inf
      }
      else{
         tmp<-qnorm(1-alpha/2)*sqrt(sigma[1]^2/n1+sigma[2]^2/n2)
         a <- zb-tmp; b <- zb+tmp
      }
      df<-n1+n2
   }
   else{
      if (var.equal ==  TRUE){
         Sw<-((n1-1)*var(x)+(n2-1)*var(y))/(n1+n2-2)
         if (side<0){
            tmp<-sqrt(Sw*(1/n1+1/n2))*qt(1-alpha,n1+n2-2)
            a <- -Inf; b <- zb+tmp
         }
         else if (side>0){
            tmp<-sqrt(Sw*(1/n1+1/n2))*qt(1-alpha,n1+n2-2)
            a <- zb-tmp; b <- Inf
         }
         else{
            tmp<-sqrt(Sw*(1/n1+1/n2))*qt(1-alpha/2,n1+n2-2)
            a <- zb-tmp; b <- zb+tmp
         }
         df<-n1+n2-2
      }
      else{
         S1<-var(x); S2<-var(y)
         nu<-(S1/n1+S2/n2)^2/(S1^2/n1^2/(n1-1)+S2^2/n2^2/(n2-1))
         if (side<0){
            tmp<-qt(1-alpha, nu)*sqrt(S1/n1+S2/n2)
            a <- -Inf; b <- zb+tmp
         }
         else if (side>0){
            tmp<-qt(1-alpha, nu)*sqrt(S1/n1+S2/n2)
            a <- zb-tmp; b <- Inf
         }
         else{
            tmp<-qt(1-alpha/2, nu)*sqrt(S1/n1+S2/n2)
            a <- zb-tmp; b <- zb+tmp
         }
         df<-nu
      }
   }
   data.frame(mean=zb, df=df, a=a, b=b)
}

求两个总体方差的情况

interval_var4<-function(x,y, 
   mu=c(Inf, Inf), side=0, alpha=0.05){ 
   n1<-length(x); n2<-length(y) 
   if (all(mu<Inf)) {
      Sx2<-1/n1*sum((x-mu[1])^2); df1<-n1
      Sy2<-1/n2*sum((y-mu[2])^2); df2<-n2
   }
   else{
      Sx2<-var(x); Sy2<-var(y); df1<-n1-1; df2<-n2-1
   }
   r<-Sx2/Sy2
   if (side<0) {
      a <- 0
      b <- r/qf(alpha,df1,df2)
   }
   else if (side>0) {
      a <- r/qf(1-alpha,df1,df2)
      b <- Inf
   }
   else{
      a<-r/qf(1-alpha/2,df1,df2)
      b<-r/qf(alpha/2,df1,df2)
   }
   data.frame(rate=r, df1=df1, df2=df2, a=a, b=b)
}