信号参数估计

一. 估计的评价准则

假设a是一个广义平稳随机信号x(n)的一个特征量，代表a的一个估计量。估计的偏差可以反应估计量与真值的接近程度，定义如下：

直观上，B越小，对a的估计就越好。理论上当样本数N趋于无穷大时，会形成逐渐无偏估计，如下：

估计的方差可以表示各次估计值相对估计均值的分散程度。估计的方差定义如下：

估计的均方误差可以综合反映估计的特性，定义如下：

如果均方误差满足如下条件，则称其为一致估计，如下：

1. 样本数
2. 

二. 一致估计

给定一致估计，证明偏差和方差都趋于零。

给定均方误差化简如下：

由条件可得：

所以可得：

最终可得偏差和方差均为0

利用代表某算法的估计值，其他算法的估计值表示如下：

如果以下不等式恒成立：

则称该估计为有效估计。

三. 估计均值

利用N代表观察次数，则平稳信号序列x(n)的观察样本如下：

由此可计算均值的估计：

3.1 偏差

首先可得：

由此可计算偏差：

所以此方式是一种无偏估计。

3.2 方差

根据定义可得：

（1）当和互不相关时，有：

代入原式子进行化简可得：

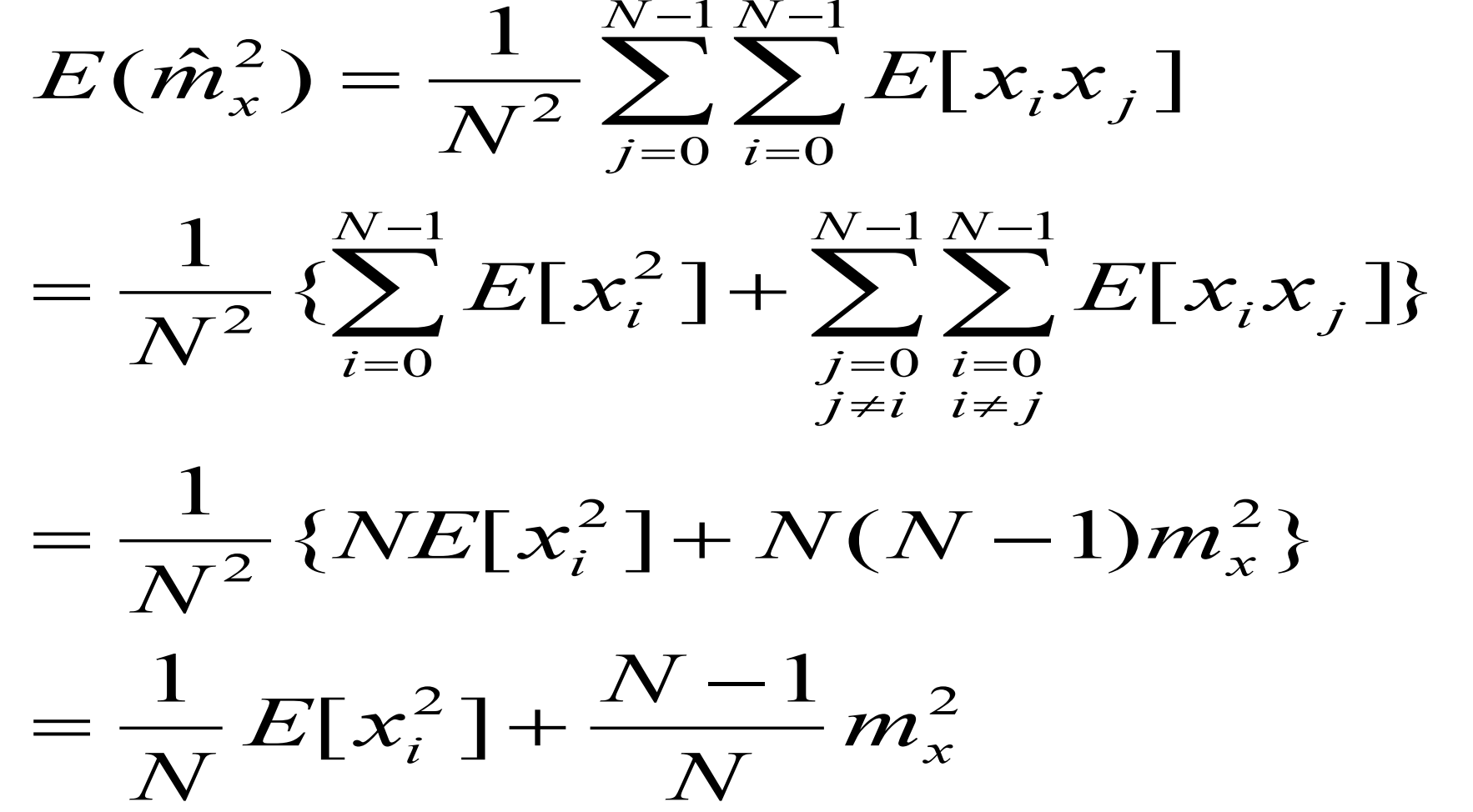
所以该估计的方差为：

可得如下极限：

所以该估计为无偏一致估计。 

（2）当和相关时，有：

进一步化简可得：
 

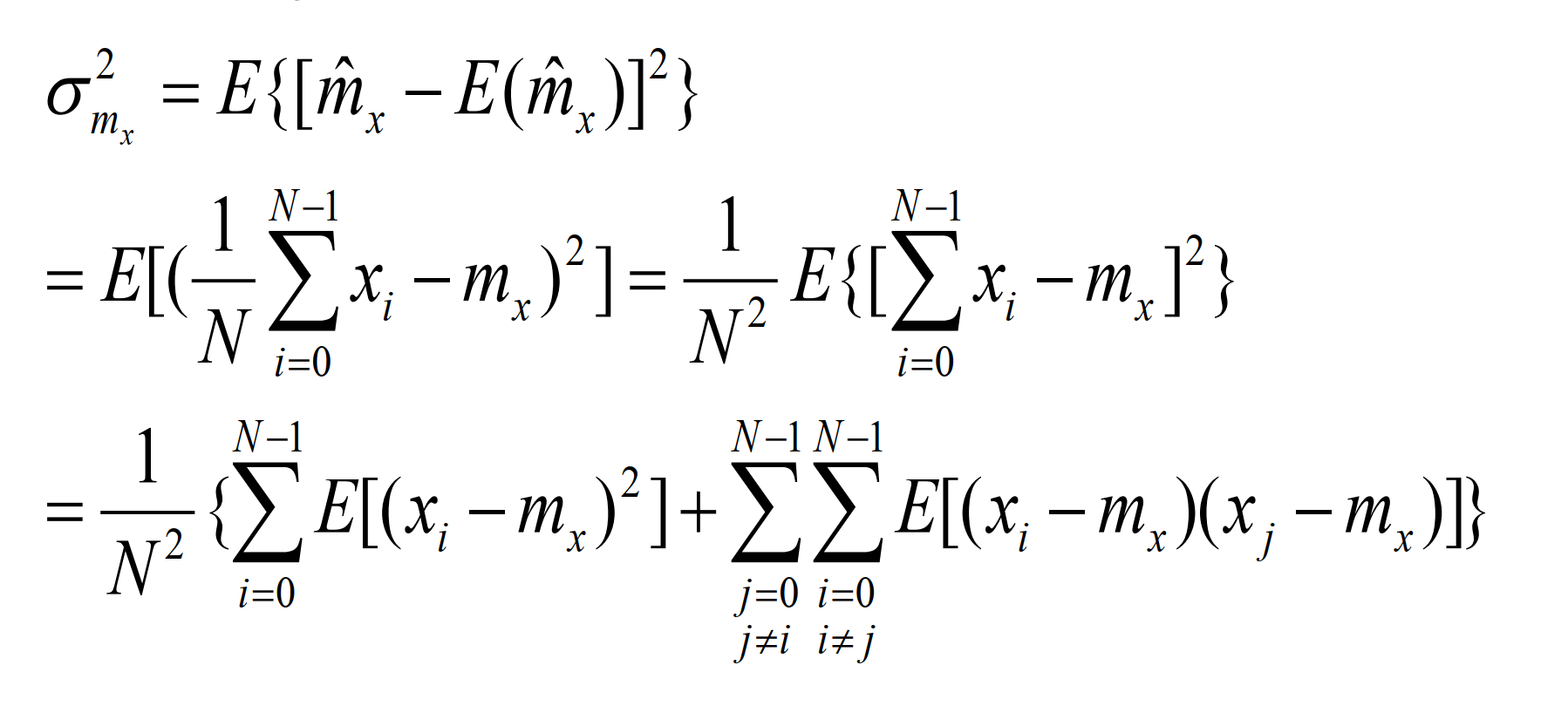
当i和j相差m时，可得：

由于在N个数据中，相距m点的数据样本有N-m对，所以可得：

 当信号数据存在相关性时，估计值的方差与协方差相关，不是一致估计，当然改变N值可以改善估计方差。

四. 估计方差

4.1 均值已知

当信号均值已知，方差估计可计算得：

证明此式子为无偏一致估计。

解：

（1）首先验证偏差：

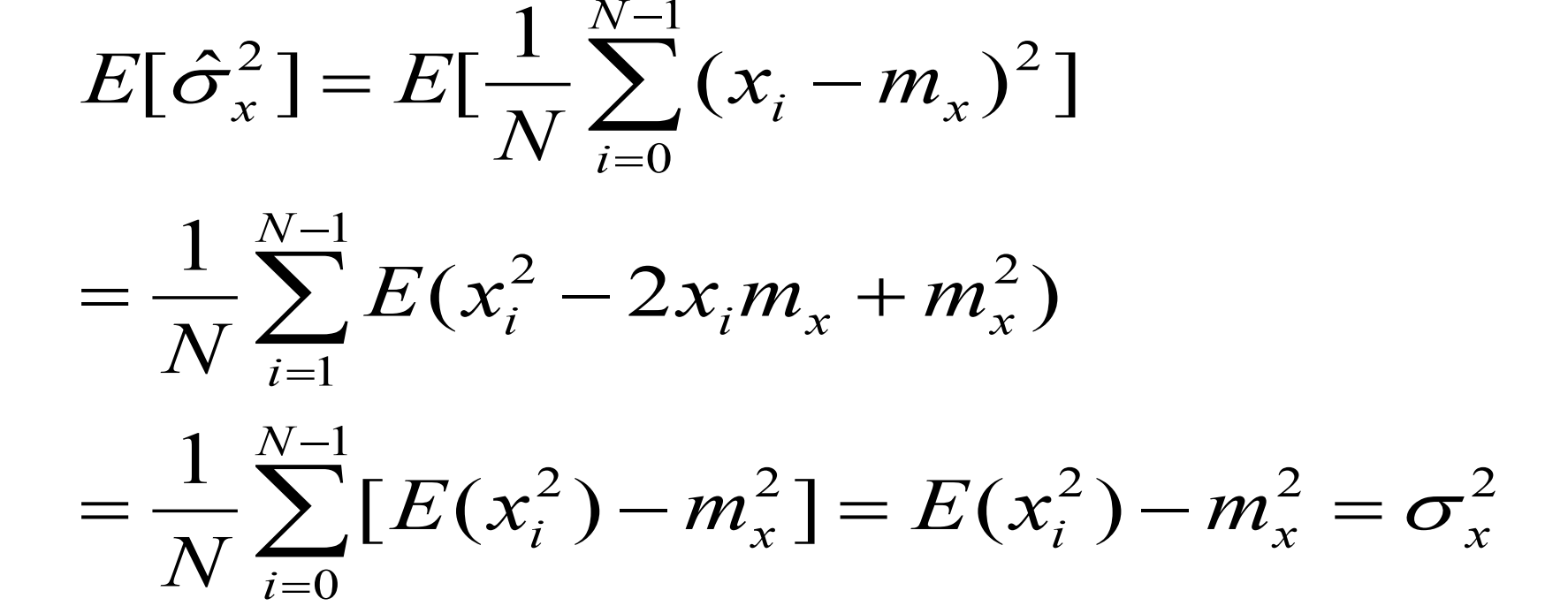
（2）接着验证一致性： 

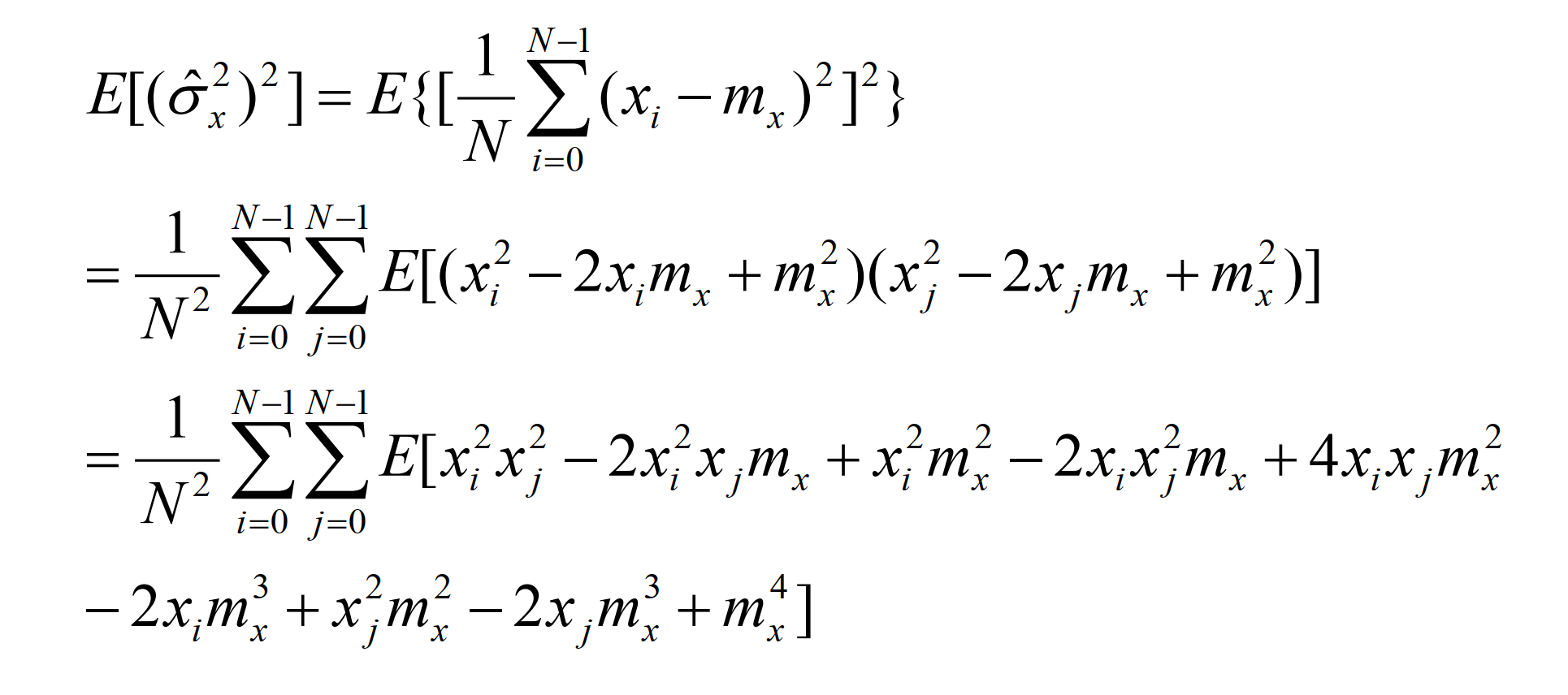
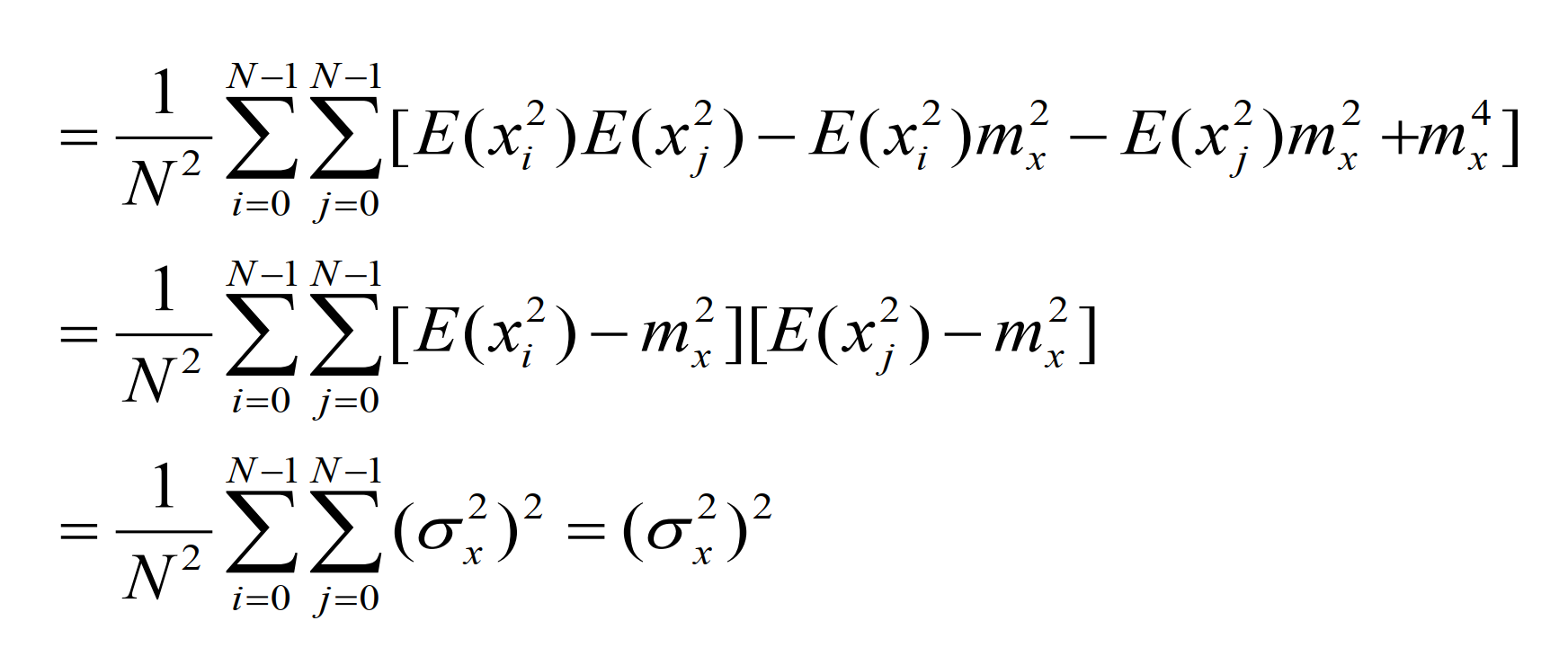
所以，估计的方差计算为：

 4.2 均值未知

当估计的均值未知时，用估值代替，方差可估计如下：

   (1) 证明该偏差为有偏估计

（2）修改原式子，形成无偏估计

解：

（1）

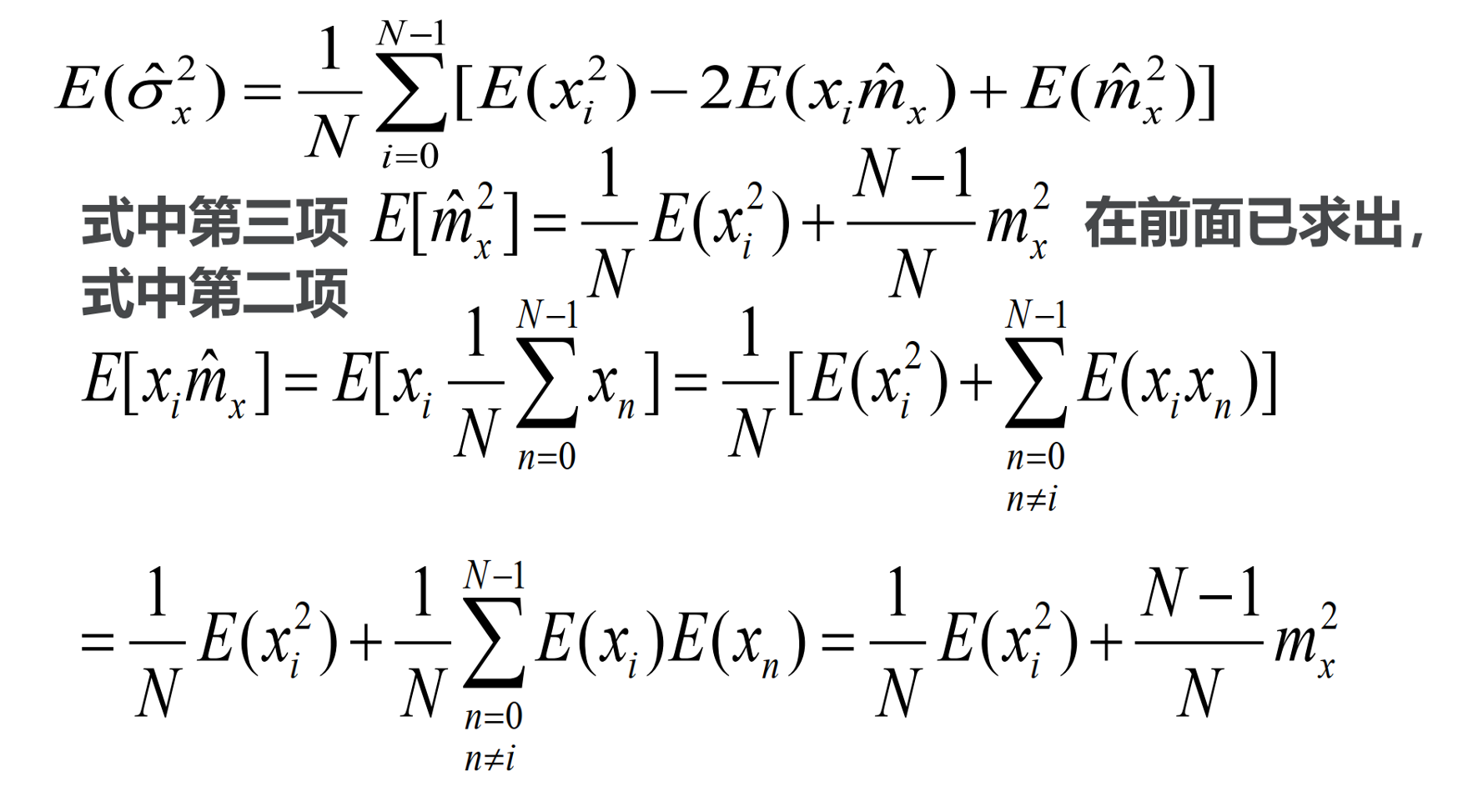
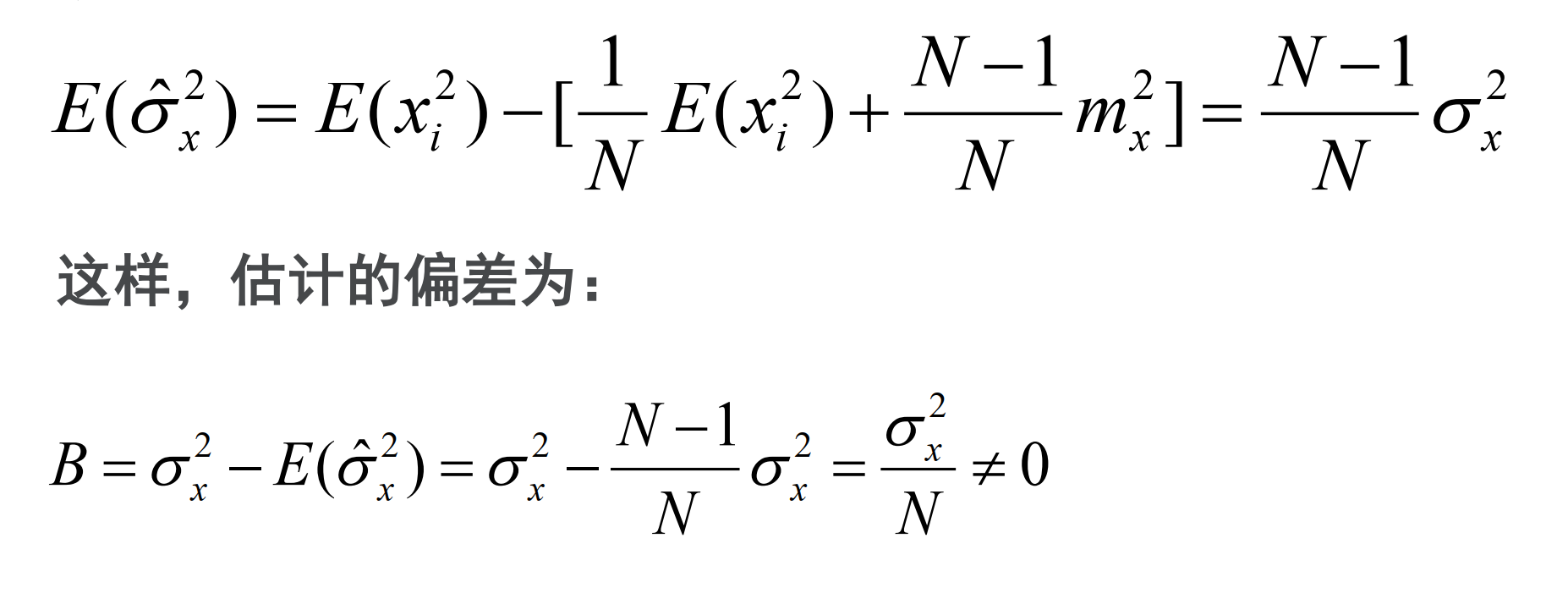
很明显此为有偏估计。

（2）无偏估计的形式如下：

以下证明此式子为无偏估计：

显然可得：

对上式子两边求均值，可得：

所以B=0，此为无偏估计。 

五. 估计自相关函数

5.1 无偏自相关函数估计

估计公式为：

首先可计算：

由此可计算偏差为：

所以此估计为无偏估计。

估计方差的计算较复杂，可以近似可得：

当N满足如下时，方差趋于0：

5.2 有偏自相关函数估计

估计公式如下：

首先可计算：

所以估计的偏差为：

接着可计算：

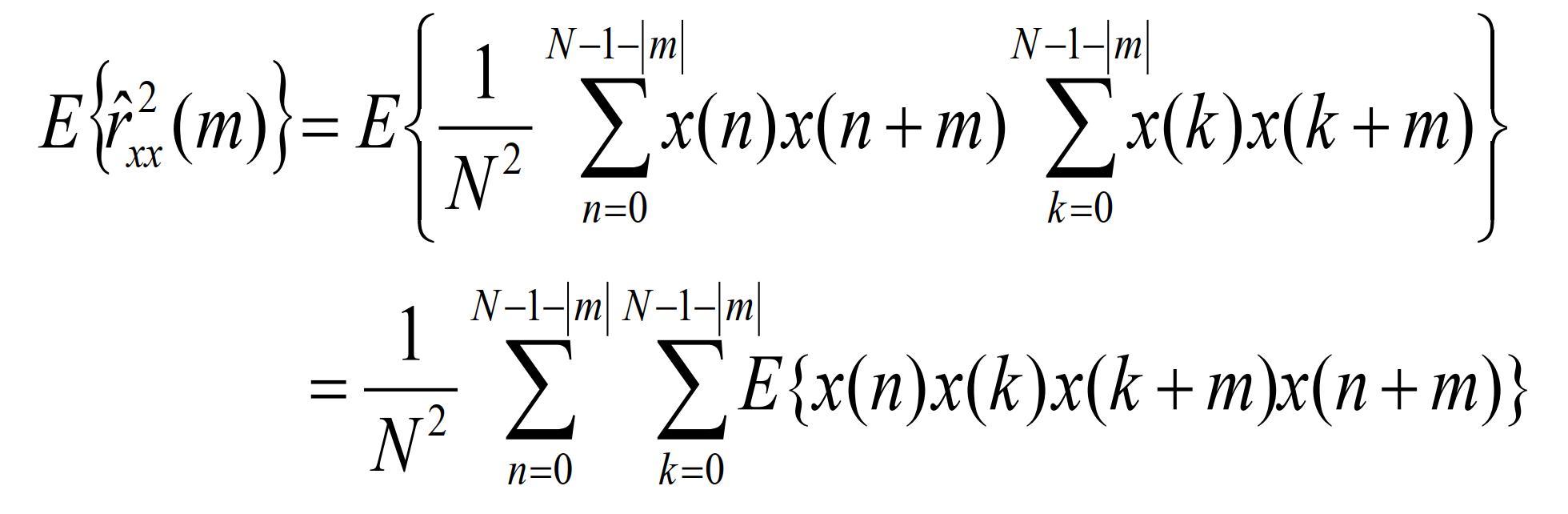
若x(n)是零均值的实高斯信号，估计的方差为：

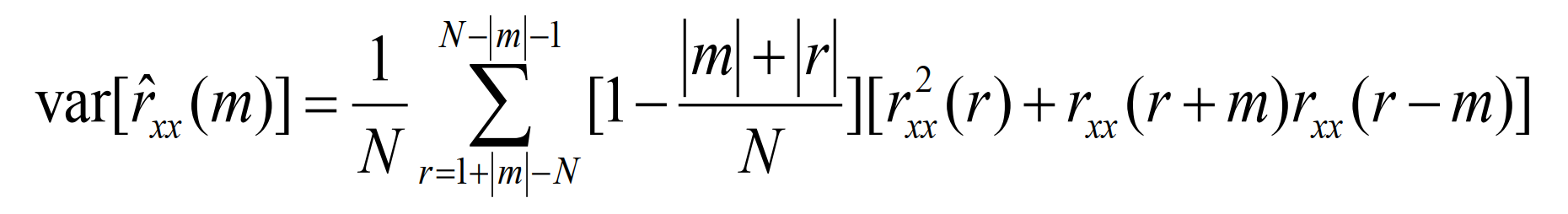
 显然可得如下极限：

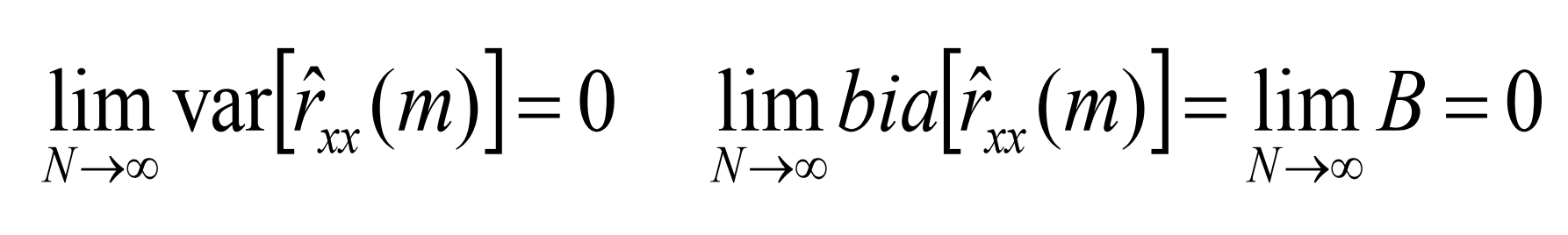
 所以对于固定的m，是的一致估计。

有偏自相关函数估计式求傅氏变换：

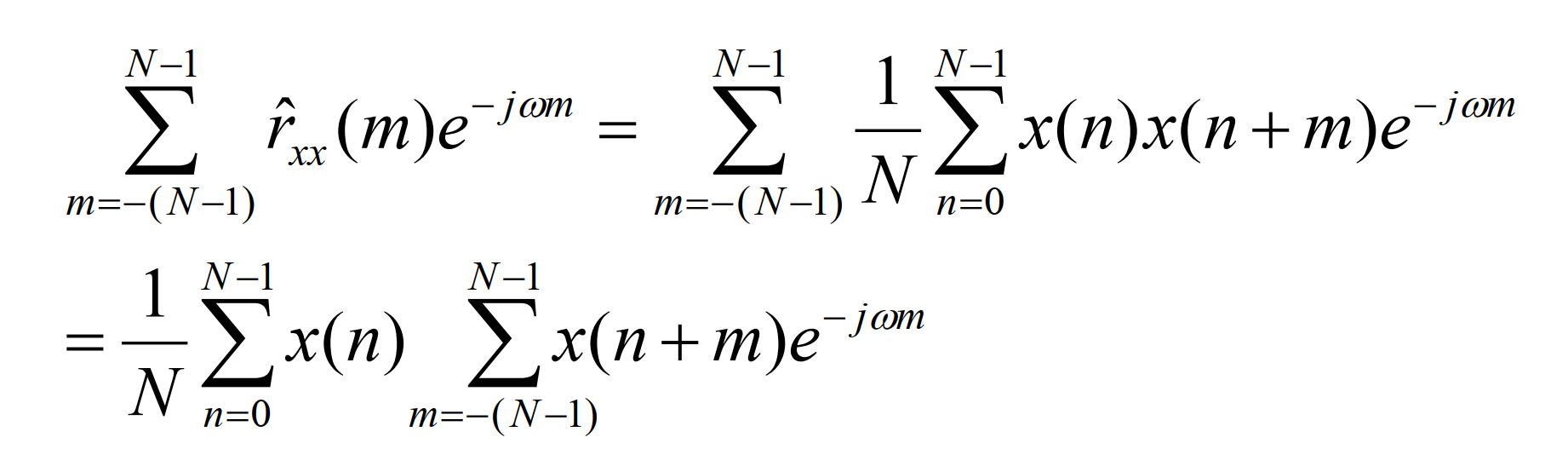
为了利用FFT计算线性卷积，可以将x(n)扩展到2N-1点的序列，如下：

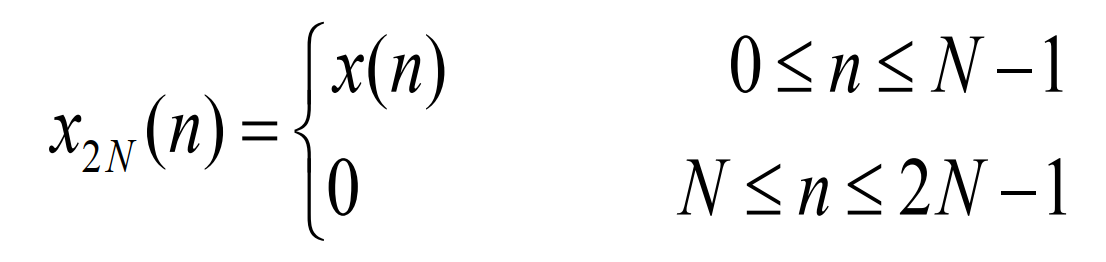
 令l=n+m，可得：

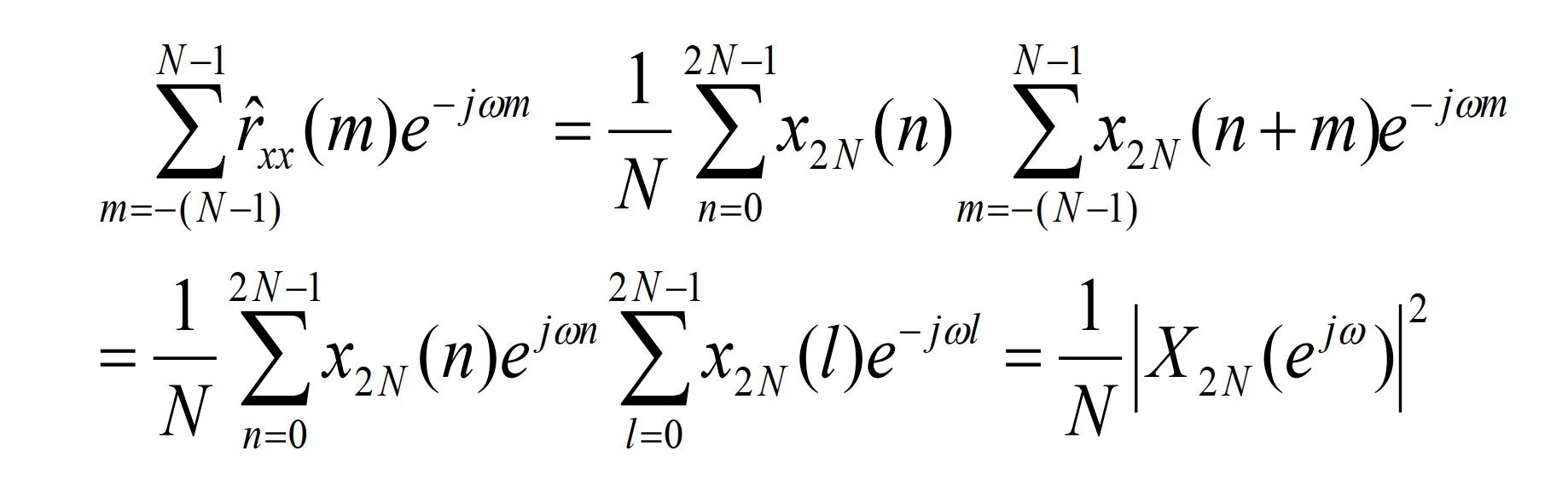
 上式子中代表有限长信号的能量谱，除以N后代表功率谱。