主要内容
- 假设检验与单样本T检验
- 两样本T检验
- 方差分析(分类变量和连续变量关系检验)
- 相关分析(两连续变量关系检验)
- 卡方检验(两分类变量关系检验)
研究两个变量是否有关系，即是否独立，如身高与性别是否有关系，男生的身高均值与女生身高的均值是不等的，它们的差不为零，但其实很多变量（如性别男、女）之间的均值之差都不为零，那它们均值之差到什么程度才认为这两个变量是有关系的，是独立的呢？
两变量关系检验方法综述
通过数据得到统计量，然后作出假设
总体 – 研究所感兴趣的所有个体组成总体
样本 – 从总体抽取的部分个体组成样本，样本用于对总体的某些指标作推断使用
统计量由样本获取，用于对总体的参数进行估计
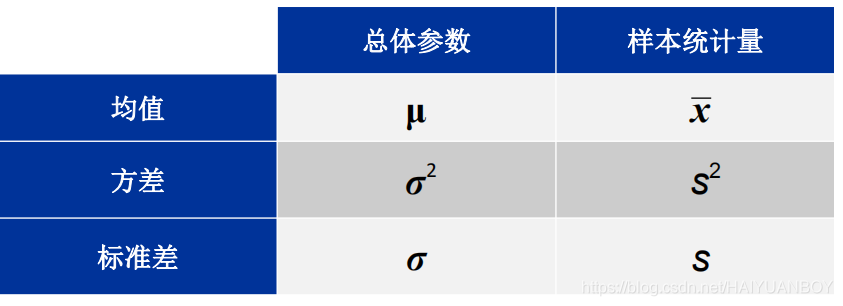
样本统计量是随机变量，因为样本是随机抽取的，但总体参数不是随机变量，是真实存在的，只是我们不知道，我们只能用样本统计量去估计它
如点估计，就直接认为样本统计量就是总体参数
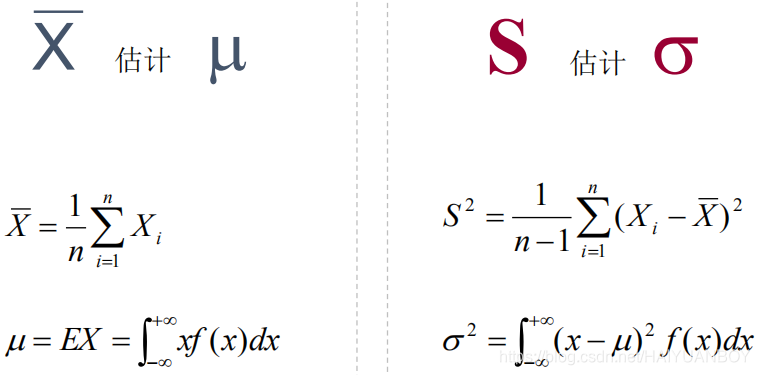
但点估计准不准呢，样本的变异来自于抽样的偏差
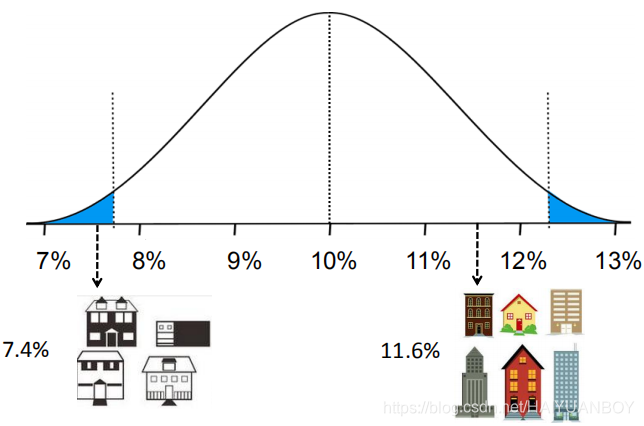
如2012年的时候房屋价格增长最快的是学区房，非学区房涨的慢，我们抽样有可能抽的涨的快的地方，计算的平均增长率就大，拿一次抽样的点代表总体就有问题了，然后置信区间就出来了
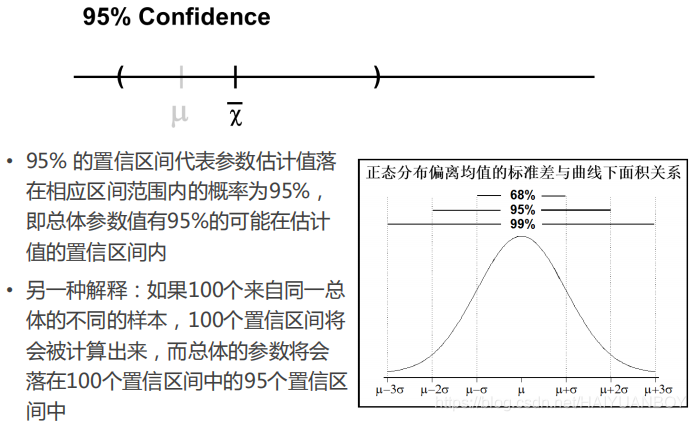
我们根据样本的均值估计出一个区间来，我们认为总体的均值是有一定的概率落在这个区间之内的，这个概率我们就叫做置信度，得到这个置信度是95%，我们就认为有95%的把握这个均值是在这个置信区间里面的。
我们怎么确定这个区间多大呢，以正太分布来说，我们以均值为中心，取两倍的标准差，得（μ-2σ，μ+2σ），通过这个方法作置信区间，我们通常的做法也就是这样，注意我们作置信区间时，中心点是样本的均值
，然后取两本的标准误
，得置信区间
，其实取几倍的标准误，就看你要多大的置信区间，但置信区间不是越大越好，置信区间大了，你估计的把握是大了，但是你作出的估计可能就没有什么实际价值，置信区间越小，给的信息量就越大，越有价值
均值的标准误差
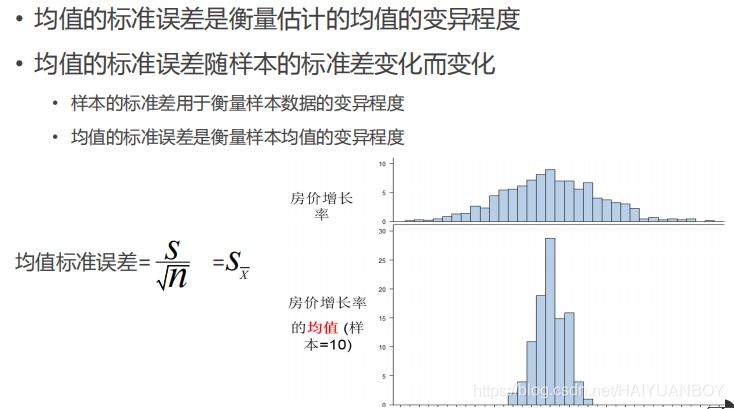
房价增长率的均值的分布是如何作出来的？比如我每次抽150个小区，150个小区能算出一个均值，抽10次，就能作出房价增长率均值的分布，然后再用这个分布计算出一个标准差，就叫做均值标准误差（简称标准误），但避免多次抽取，科学家发现了这个公式
2012年北京市9月份房价同比增长率案例
# - 数据说明：本数据是地区房价增长率数据
# - 名称-中文含义
# - dis_name-小区名称
# - rate-房价同比增长率
#%% 2012年北京市9月份房价同比增长率
import os
os.chdir(r"D:\pydata")
# In[1]:
import pandas as pd
house_price_gr = pd.read_csv(r'house_price_gr.csv', encoding='gbk')
house_price_gr.head()
Out[2]:
dis_name rate
0 东城区甘南小区 0.169747
1 东城区察慈小区 0.165484
2 东城区胡家园小区 0.141358
3 东城区台基厂小区 0.063197
4 东城区青年湖小区 0.101528
# 进行描述性统计分析
# In[2]:
house_price_gr.describe(include='all')
Out[3]:
dis_name rate
count 150 150.000000
unique 150 NaN
top 顺义区双裕小区 NaN
freq 1 NaN
mean NaN 0.110061
std NaN 0.041333
min NaN 0.029540
25% NaN 0.080027
50% NaN 0.104908
75% NaN 0.140066
max NaN 0.243743
get_ipython().magic('matplotlib inline')
import seaborn as sns
from scipy import stats
sns.distplot(house_price_gr.rate, kde=True, fit=stats.norm) # Histograph黑色的线是正太分布，蓝色的线是我们样本的分布
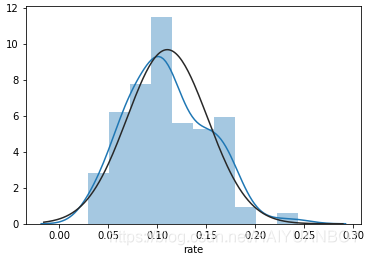
# Q-Q
# In[4]:
import statsmodels.api as sm
from matplotlib import pyplot as plt
fig = sm.qqplot(house_price_gr.rate, fit=True, line='45')
fig.show()蓝点是我们的数据，红线是正太分布
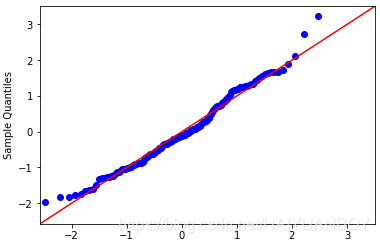
house_price_gr.plot(kind='box') # Box Plots
# 置信度区间估计
# In[6]:
# 计算标准误
se = house_price_gr.rate.std() / len(house_price_gr) ** 0.5
# 置信区间下界，95%的置信区间准确来说是1.98倍的标准误，而不是2倍的标准误
LB = house_price_gr.rate.mean() - 1.98 * se
# 置信区间上界
UB = house_price_gr.rate.mean() + 1.98 * se
(LB, UB)
Out[7]: (0.10337882853175007, 0.11674316487209624)
# 如果要求任意置信度下的置信区间的话，可以自己编一个函数
def confint(x, alpha=0.05):
n = len(x)
xb = x.mean()
df = n-1
tmp = (x.std() / n ** 0.5) * stats.t.ppf(1-alpha/2, df)
return {'Mean': xb, 'Degree of Freedom':df, 'LB':xb-tmp, 'UB':xb+tmp}
confint(house_price_gr.rate, 0.05)抽取150个小区的9月份的房价同比增长率，得到增长率的均值是11%，有95%的把握认为整个北京市9月份的房价同比增长率在10.3%到11.6%之间，小于等于10.3%的概率不超过2.5%
如果数据是正太分布的，那么它的均值一定是正太分布的，但如果数据不是正太分布的呢。
中心极限定理
根据中心极限定理，当我们的数据是独立同分布的，并且样本量足够大的情况下，“足够大”表示大于30 个样本，那么它的均值渐进地服从正太分布，即近似正太。如果数据严重偏态，则需要更多的样本，如果数据本身是对称则不用
当抽样越来越多的时候，它的均值越来越接近正太分布
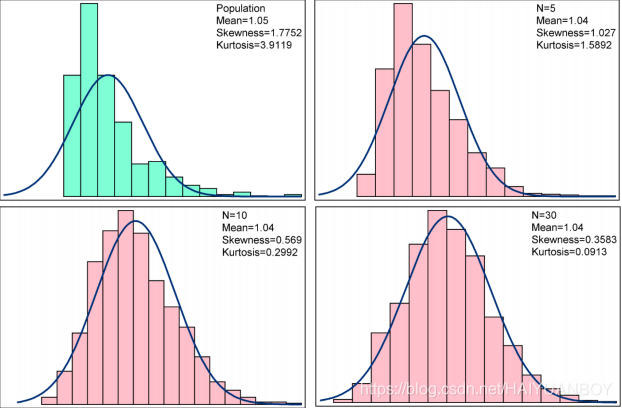
有了中心极限定理，我们置信区间的取法就有依据了