引入
出发点:我们以前在参数估计中都是先假设样本点的分布有一个概率密度函数形式,比如高斯分布,然后从样本中估计参数。但是,有可能根本不是,所以也有非参数法研究的必要,比如我们中学就学过频率分布直方图,但是缺点在于我们要记录每一组的边界和每一组的数量,要保存很多参数。
这个思想过渡很重要,因为如果我们样本足够多,想象一下,频率分布直方图每一组的组距特别小,组特别多,这不就是在逼近样本点的真实概率密度函数了吗?那如果真实分布不是高斯分布,而是一个V型的分布,那非参数法就估计得很不错啊,频率分布直方图可以把这个信息表达出来。
一般地,样本足够多的时候其可以表示出任意类型的分布!
基础知识
既然非参数法这么好,下面开始介绍基础建筑。
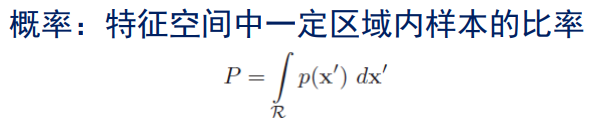
这个很好理解,R是指这个一定区域, p ( x ′ ) p(x^{'}) p(x′)是概率密度函数。就有点像二维的情况。
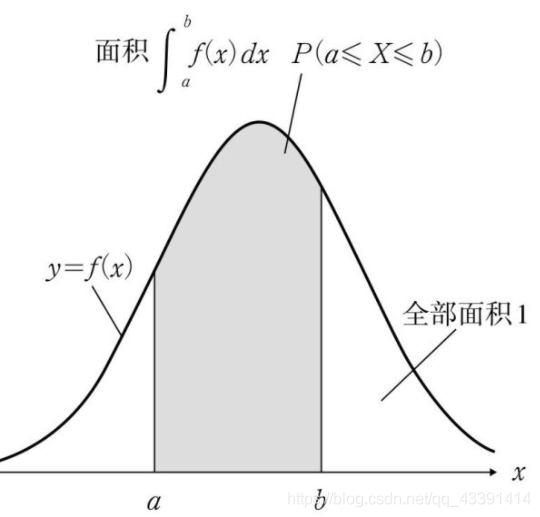
所以上上幅图求的是样本落在R空间的概率。
我们继续下一个知识点。
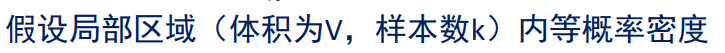
该区域等概率密度,那么不就可以算该区域的概率密度了嘛!
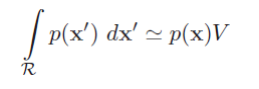
而这个由最前面的概念知道,这个是在样本落在空间R中的概率,我们假设R里面有k个样本,整个空间有n个样本,那么样本落在空间R中的概率就是 k n \frac{k}{n} nk。
从而求得空间R中的概率密度函数为
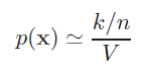
我们要估计样本的概率密度函数,但是这个V如何选择呢?这就有点像你要画个频率分布直方图,组距选择多大呢?显然,我们都认为:如果样本数无穷多个,那么我们空间V就选小点,这样就可以表示得更加精确。就像下面这样:

因此:

解释:上面的 p ( x ) p(x) p(x)表示的是真实概率密度函数,我们希望可以逼近它。
上面都是理论,下面探讨细节。
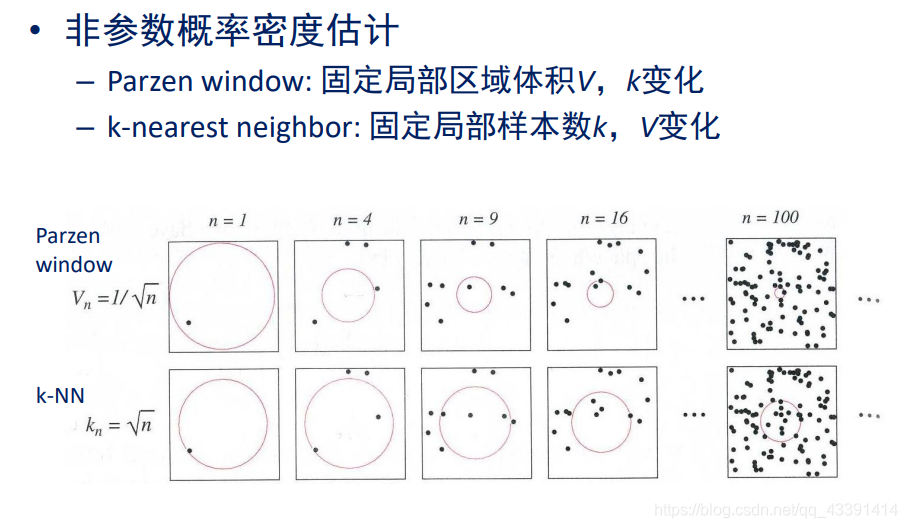
上面的大家好好看一下就行,没懂也没关系,后面会展开介绍。
Parzen窗估计
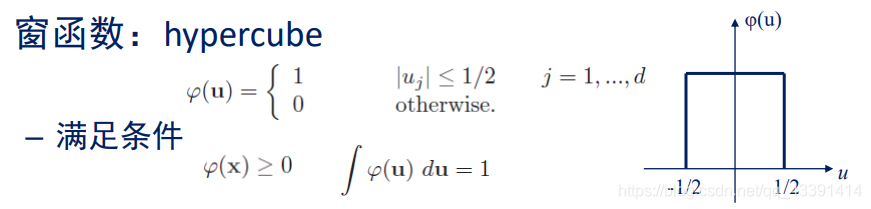
解释:这里拓展到了高维的情况,但是低维也适用。样本空间是d维。
然后定义了一个窗函数,即在落在窗口内则函数值为1,否则为0。这个窗口在一维是一个关于原点对称的线段,长度为1;在二维是一个关于原点中心对称的正方形,面积为1;在三维是一个关于原点中心对称的正方体,体积为1。
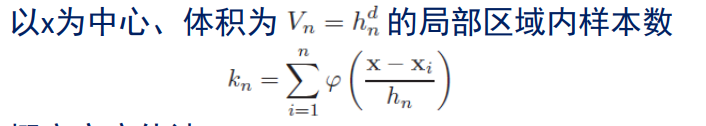
注:上面 h n h_n hn是边长。
我们现在用上窗函数了,即对于任意一个样本点 x i x_i xi,只要满足向量 x − x i x-x_i x−xi的某一个维度 < = h n / 2 <=h_n/2 <=hn/2,那么值为1(相当于计数器加1),这不正是我们要求的该区域内样本数吗?
然后代入到之前的公式里。
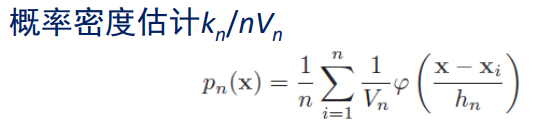
我们发现,我们上面用的窗函数是一个超立方体内为1,我们希望推广,找到一些其他的窗函数,但要满足

即:

为什么窗函数需要满足积分为1?其实主要是因为概率密度函数积分要为1,所以推得窗函数也要。
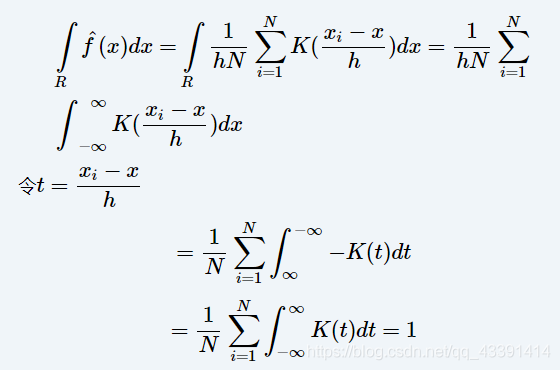

除了之前的方窗函数,我们也经常选用如下形式的高斯窗函数。
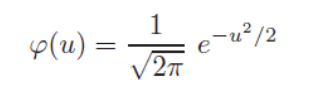
然后用这个来估计样本概率密度。(我们先假设1维的情况下)
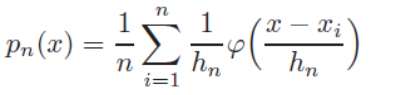
例子:下面展示的是只有一个样本点,我们使用高斯窗函数,选用不同的窗口大小得到的估计结果。
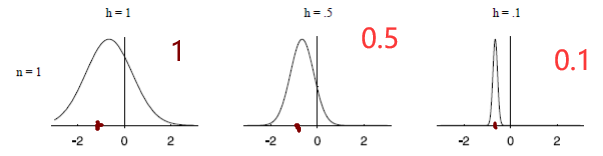
请注意,这里的纵轴没有标刻度,实际上 h = 0.1 h=0.1 h=0.1的时候函数是最高的,但是很窄,方差小。即:

例子:
假设有一批样本点,我们选定一个 h n h_n hn,有如下结果。
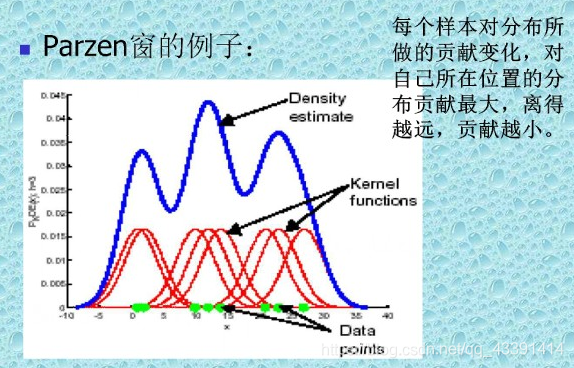
解释:
显然,估计的方法是:对每一个样本点的头上套一个窗(红色),然后叠加起来求平均,就是最终的样本概率密度了(蓝色)。(上面展示的图是直接相加,没有求平均,为了好看而已)
显然上面的窗就是下面这个式子(对比 p n ( x ) p_n(x) pn(x)的表达式即可):
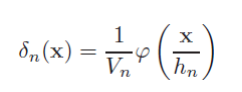
注意到,这个式子积分也是为1的!自己可以推一下。
我们知道:直观上样本数量无穷大的时候,然后我们把窗口设得比较小的时候,可以拟合真实的概率密度函数,下面也有一个理论证明:

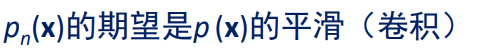
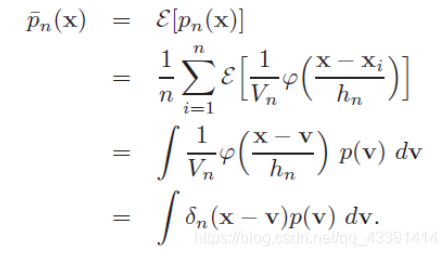
上述求和除以n没有了是因为:

得到上述的积分等式之后,我们有结论:
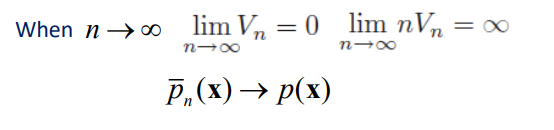
我们继续举个分类的例子
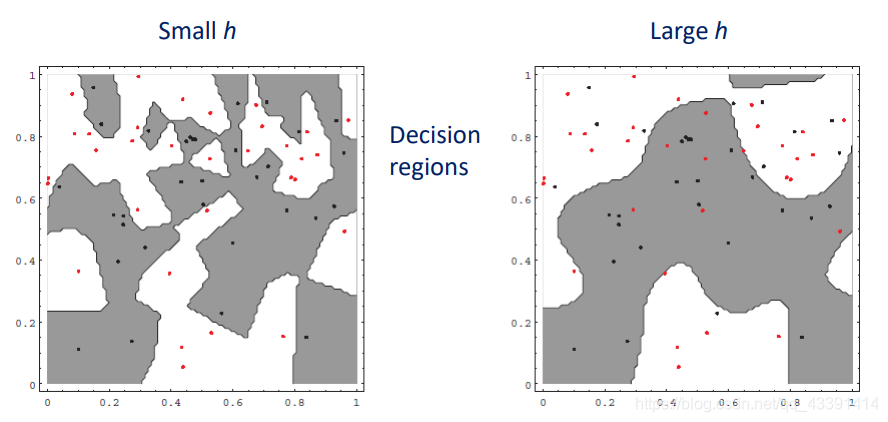
使用parzen窗估计做法很简单,就是对每一类拟合一个样本概率密度函数,然后得到分界面如上所示。区别在于,在拟合样本概率密度的时候,选择窗口的大小不同会导致上面的不同,选择小的窗口可以带来过拟合。

改进办法:根据局部密度采用自适应窗口大小。

K近邻估计
如何计算样本概率密度?

个人觉得V也是一个与k有关的数,k越大,V也越大。
那么如何选择k呢?
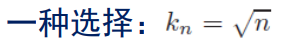
例子:
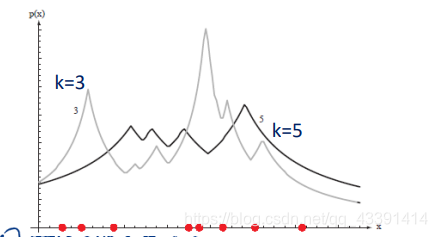
有人难以理解,为什么是这样,我们可以假设k=1,那么变成最近邻,在任意样本点 x i x_i xi上面,其概率密度函数为 p n ( x i ) = 1 / n 0 = ∞ p_n(x_i)=\frac{1/n}{0}=\infty pn(xi)=01/n=∞。即k越小越突兀。为什么 V n V_n Vn为0?因为对于 x i x_i xi而言,最近的样本点是 x i x_i xi,所以,在一维平面上,有 V n = x i − x i = 0 V_n=x_i-x_i=0 Vn=xi−xi=0。即 V n V_n Vn是指最近的那个样本点到 x x x的距离的两倍(在一维中是距离或叫线段长度)。
一般地,一维中有:
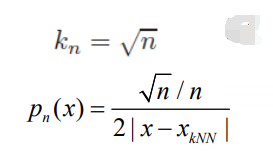
x k N N x_{kNN} xkNN是指离 x x x第k个最近的点。
拓展,在二维中 V n V_n Vn是圆的面积,三维中是球体的体积。
使用KNN来贝叶斯分类:

非常精彩,红色公式中下面是 p ( x ) p(x) p(x),上面是 p ( x , w i ) p(x,w_i) p(x,wi)联合概率密度。而且,这和我们的投票方法是一样的, k i k_i ki中谁大就分给谁。
当然还有使用KNN分类的办法,上面不是唯一的。
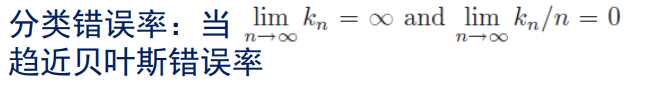
原因很简单,因为 n n n趋于无穷的时候, p ( x ) p(x) p(x)估计准确,所以趋近于贝叶斯错误率。
下面介绍一个特殊情况:最近邻分类。
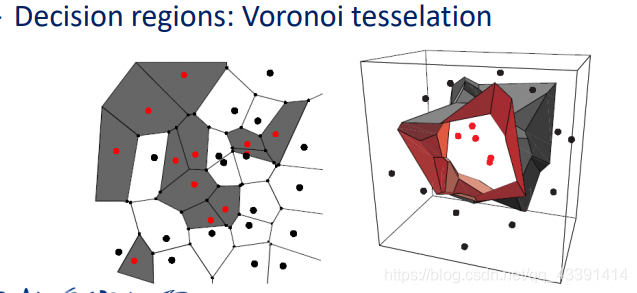
K近邻的快速计算
先计算部分欧式距离,总共d维,先计算前r维的距离。
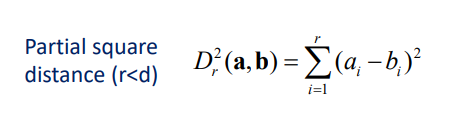
假设:我们是快速计算最近邻。
那么快速计算的方法是:先计算x对第一个样本的全部距离,设为最小值,然后计算与第二个样本的部分距离,一旦超过最小值,后面的部分距离就不用算了。
再介绍一个思路
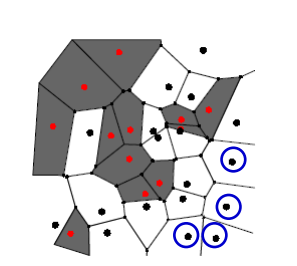
即先将样本预处理,将圆形黑色删除,因为删除不会导致误判!
还有一些其他的算法,比如人工智能中很多非常重要的搜索算法,这里可能用得上!总之,应该意识到,快速计算非常重要,否则如果100万个点,k近邻很慢。
Parzen窗方法的快速计算


其中:
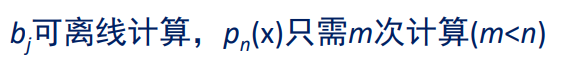
这样,预测x的类别的时候就方便了。 b j b_j bj早就算好了,算个 p n ( x ) p_n(x) pn(x)就行。
例子:

展开到第2项。
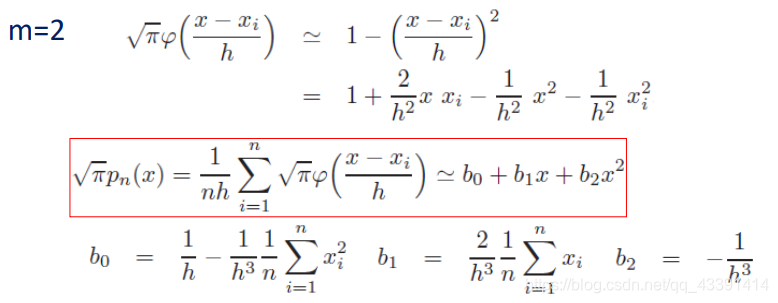
从而提前计算好 b 1 , b 2 , b 0 b_1,b_2,b_0 b1,b2,b0即可。
总结
非参数估计和参数估计有联系但有很大区别,两者都非常重要。前者假定有一个概率密度函数形式,后者可以处理具有任意概率分布形式的数据。
讨论:非参数估计中,在我们对所有训练样本非参数估计后,按理可以得到一个概率密度函数,一般这个是一个具有非常多参数的函数,我们可以保存起来,然后丢弃所有样本,就像在参数估计一样。但是也要注意到,正文中两个快速计算方法都是基于局部空间临时计算概率密度,即所有样本都还要保留,可见这是另一种做法。