矩阵论: 第五章 特征值的估计 与 (非齐次方程组相关的)广义逆矩阵 (finally)

特征值的界估计

最小范数解 和 最小二乘解

广义逆

特征值的界估计

复数矩阵
厄米特矩阵: 共轭转置矩阵 和 原矩阵的关系 特征值是实数
反厄米特矩阵: 共轭转置矩阵 和 原矩阵的关系 特征值是虚数

正规矩阵:

1. 与自己的共轭转置矩阵对应的 复系数方块矩阵
2. 正规矩阵 ------> 经过一个酉变换 ----> 对角矩阵，
3. 所有可在经过一个酉变换后变为对角矩阵的矩阵都是正规矩阵

什么是酉矩阵; 酉矩阵的特征值都是 模为1 的复数
下图中的* 代表的是矩阵的共轭转置矩阵

圆盘定理

行盖尔圆: 的求法
特征值和盖尔圆的关系
连通部分

谱半径的估计

复数域上的任意n阶方针的谱半径都不超过A的任一范数(1, 无穷, 2)
2范数: 复数矩阵 * 其共轭转置矩阵 的 最大特征值 再开方

若A 是n阶正规矩阵, 那么谱半径等于矩阵A的2范数

广义逆矩阵 与 线性方程组的解

1. {1}-广义逆 (广义逆矩阵)

A: mn
G: nm
G是A 的广义逆
AX = B(B 是任意给定的 m*1的矩阵) 有解, 那么就称为 X = GB 也一定是方程组的解

判定的充要条件: AGA = A, 则称为G为A的 {1}-广义逆
一般性: 矩阵A为mn, 且 rankA = r, 则 A的{1} - 广义逆可以表示为

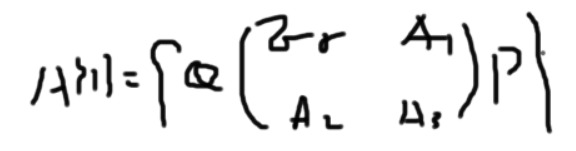
这里的Er为r维的单位矩阵 A1 A2 A3为任意矩阵,但是要满足整个矩阵为nm

m = n = r, 当矩阵A 是可逆的时候, A 的广义逆为 A的逆矩阵

A的广义逆存在, 当方程组AX = B有解的时候, 通解可以表示为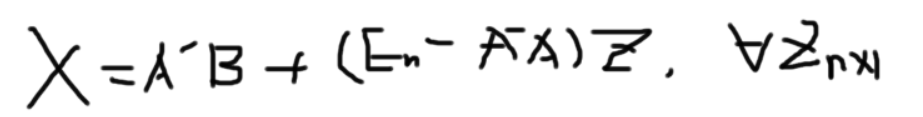

AX = B中的最小范数解和最小二乘解

广义逆 的类别

若 G 满足 (1), 则为 {1}-广义逆

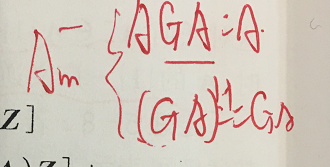
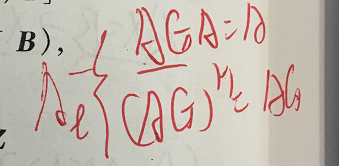
广义逆矩阵A+

对于任意一个矩阵A m*n 的. 其广义逆矩阵 A+ 存在且唯一 ==> 其他三类都是存在的

若A是可逆的, 那么A 的广义逆矩阵 = A 的{1}-广义逆 = A的逆矩阵

AX = B的极小最小二乘解 为 X = 广义逆矩阵 * B

summary

m = n = r:
若A是可逆的, 那么A 的广义逆矩阵 = A 的{1}-广义逆 = A的逆矩阵
当矩阵A 是可逆的时候, A 的广义逆为 A的逆矩阵