堆的概念
堆实际上还是一棵二叉树,不过它还满足下列两点要求:
(1)堆是一棵完全二叉树。(关于完全二叉树的定义见:数据结构------二叉树的面试题)
(2)堆中元素满足:对任一棵树来说,它的根节点的值比它的左,右孩子都大或都小(注意:左右孩子之间没有明确的大小关系)。
根节点的值比它的左,右孩子元素都大的堆称为大(根)堆。
根节点的值比它的左,右孩子元素都小的堆称为小(根)堆。
堆的相关操作
在下文中将实现堆的一些相关操作:
(1)初始化(大/小)堆
(2)在堆中插入元素
(3)删除堆顶元素
(4)清空堆
(5)统计堆中的结点个数
(6)销毁堆
(7)根据堆来对一个数组进行排序
1. 堆的结构定义
因为堆是一棵完全二叉树。所以可以将堆用数组来进行表示。其中堆中根节点与左右孩子结点的下标满足如下关系(假设根节点的下标为i):左孩子节点下标:2*i+1,右孩子结点下标:2*i+2。所以根据下标可以很方便的对堆中的各节点进行操作。
数组最大容纳的元素个数也需要提前规定好。同时还需要定义一个size来表示堆中实际节点的格式。
根有大堆和小堆之分,所以在堆进行定义时,可以定义一个函数指针来确定是大堆还是小堆。
因此,结构定义如下:
typedef char HeapType;
#define MAXSIZE 100
typedef int (*Compare)(HeapType a,HeapType b);//定义一个函数指针用于表示是大堆还是小堆
typedef struct Heap
{
HeapType data[MAXSIZE];
size_t size;//堆中实际的节点个数
Compare cmp;//该参数用于判断是大堆还是小堆,在实际应用,由用户自己传参确定是创建大堆还是小堆
}Heap;
2. 堆的初始化
初始时,堆中元素应为0,且创建大堆还是小堆,需用户进行传参决定。
//堆的初始化:初始化时说明该堆是大堆还是小堆
void HeapInit(Heap* heap,Compare cmp)
{
if(heap == NULL)
{
//非法输入
return;
}
heap->size = 0;//初始时堆中节点个数为0
heap->cmp = cmp;//该堆是大堆还是小堆由用户传入的参数决定
return;
}
如果传参如下函数参数,表示是大堆:
int Greater(HeapType a,HeapType b)
{
return a > b? 1:0;
}
如果传参如下函数参数,表示是小堆:
int Less(HeapType a,HeapType b)
{
return a < b? 1:0;//如果a小于b表示是小堆
}
3. 在堆中插入元素(假设为小堆)
在插入之前首先要判断数组是否已经达到最大长度,如果达到了,就不能在进行插入了。否则,进行如下操作。
然后,因为堆在插入之前满足堆的上述两个条件,堆在插入一个元素之后也应满足这两个条件,使之还为堆。
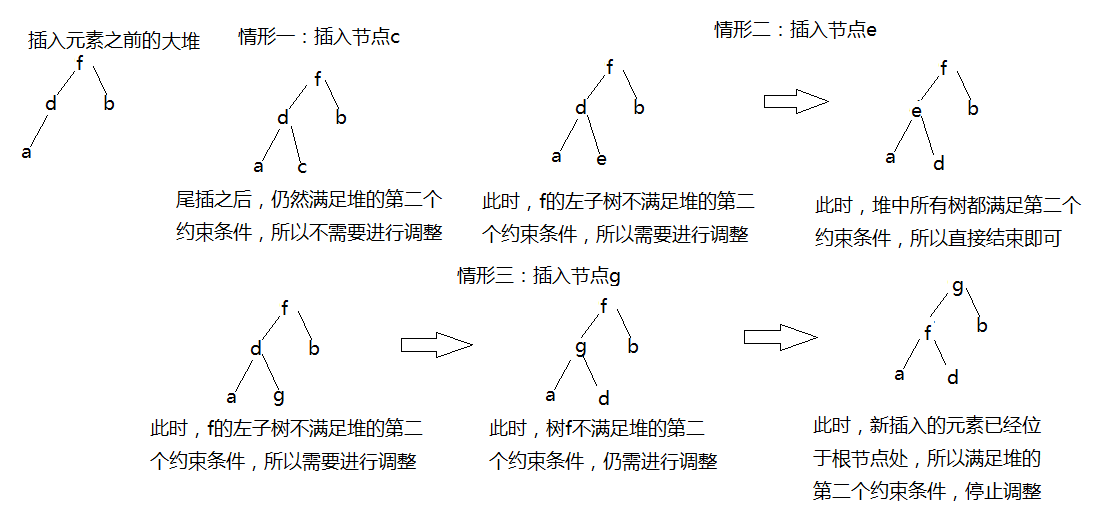
如下图所示的三种情况:
根据上图可以将思路总结如下:
因为堆是由数组的形式来进行存储时,而数组的实际长度size即为堆中最后一个元素的下一个元素的下标,所以此时可以对数组进行尾插来往堆中插入元素。插入之后,堆还是一棵完全二叉树。但是由于插入的元素值大小不确定,所以不一定会满足堆的第二个条件。
在插入元素之后为满足堆的第二个约束条件,需要做如下操作(假设是大堆):
(1)将新插入的元素下标定义为child,根据child计算新插入元素双亲结点的下标parent
(2)因为大堆中根节点的值比两个孩子节点的值均大。所以,将child处的元素与parent处的元素进行比较,如果child处的值小于parent处的值,此时,满足大堆的第二个条件,所以无需进行调整,直接返回即可。
(3)如果不满足(2),就要交换child处的值和parent处的值。然后,将child的值更新为parent,parent在根据新的child计算进行更新。再次进行比较,循环(2)~(3)不断进行上浮式调整。
(4)如果child的值已经更新到0了,说明此时整个堆的根结点已经替换为最大值,所以直接返回即可。
代码如下:
//时间复杂度为:logn
void HeapInsert(Heap* heap,HeapType value)
{
if(heap == NULL)
{
//非法输入
return;
}
if(heap->size >= MAXSIZE)
{
//堆满无法插入
return;
}
//直接对数组进行尾插,尾插完已经保证还是完全二叉树
heap->data[heap->size++] = value;
//接下来要做的就是保证堆中任意树的根节点比左右子树大或小,
//因此需要将新插入的节点进行上浮式调整,调整的初始位置为新插入的节点位置
AdjustUp(heap,heap->size - 1);
//调整结束之后就保证了该二叉树还是一个堆
return;
}
上浮式调整函数如下:
//对堆中元素进行上浮式调整:时间复杂度为:logn
void AdjustUp(Heap* heap,size_t start_loc)
{
if(heap == NULL)
{
//非法输入
return;
}
//在调整的过程中,需要不断的比较树的根节点与孩子节点的大小
//如果不满足比较条件,就一直往上浮
//如果满足条件,就停止调整
//直到到达树的根节点为止
size_t child = start_loc;//从新插入的结点下标处开始调整
size_t parent = (child - 1)/2;
while(1)
{
if(child == 0)
{
//已经调整的树的根节点位置
break;
}
//不满足比较条件
if(heap->cmp(heap->data[parent],heap->data[child]) == 0)
{
//交换孩子与根节点的元素
Swap(&heap->data[parent],&heap->data[child]);
//更新孩子节点与根节点的位置下标,判断是否要继续上浮
child = parent;
parent = (child - 1)/2;
}
else
{
//此时满足了比较条件,就不需要再进行交换并上浮了,所以直接返回即可
break;
}
}
return;
}
元素交换函数如下:
void Swap(HeapType* a,HeapType* b)
{
//交换堆中的元素
HeapType tmp;
tmp = *a;
*a = *b;
*b = tmp;
return;
}
在上述函数中,因为上浮调整函数每次都要除2遍历到上一次,所以时间复杂度为:log2(n),因此,插入元素的函数时间复杂度也为:log2(n)。
4. 在堆中删除堆顶元素(假设为大堆)
在删除元素之前,首先要判断数组元素是否为空,为空则删除失败。否则对其进行删除操作。
在删除元素之后,也应该满足堆的两个约束条件。
(1)为使删除堆顶元素之后,还是一棵完全二叉树。因为堆是由由数组进行存储的,所以直接删除数组最后一个元素,则还是一棵完全二叉树,但最后一个元素不一定是堆顶元素,所以需要先将堆顶元素与数组尾元素交换,然后在size--进行尾删
(2)尾删之后,不一定满足堆的第二个约束条件,因为此时的堆顶元素可能已经变成了比它左右子树还小的元素。
(3)所以,首先要从根节点开始,比较根结点与其左右孩子三者之中的最大值。
a)如果最大值仍为根节点,则已经满足条件,无需调整直接返回即可
b)如果右孩子存在且最大值为右孩子,则将根结点与右孩子进行交换
c)如果左孩子存在且最大值为左孩子,则将根节点与左孩子进行交换
(4)在上述的b)中交换完成之后,根节点的右子树不一定满足约束条件,所以还需对右子树进行(3)的判断。上述的c)同理。所以需要一直不断往下判断调整。一直调整到将最初的根节点交换到树的最后一层上,此时,该结点没有左右子树了,一定是他所在子树的最大值,所以停止调整。
代码如下:
//删除堆顶元素,时间复杂度为:logn
void HeapErase(Heap* heap)
{
if(heap == NULL)
{
//非法输入
return;
}
if(heap->size == 0)
{
//空堆无法进行删除
return;
}
//先将堆顶元素与堆尾元素交换,再尾删堆顶元素
Swap(&heap->data[0],&heap->data[heap->size - 1]);
--heap->size;
//再对新的堆顶元素进行下沉式调整,从堆顶位置开始调整
AdjustDown(heap,0);
//调整结束之后就保证了该二叉树还是一个堆
return;
}
下沉式调整函数:
//对堆进行下沉式调整
//时间复杂度为:logn
void AdjustDown(Heap* heap,size_t start_loc)
{
if(heap == NULL)
{
//非法输入
return;
}
//如果是大堆,堆顶元素应为根节点,左,右孩子中的最大值
//所以先比较找到左,右孩子中的最大值,
//然后再将根节点和孩子中的最大值进行比较,如果根节点比最大值小,就交换这两个节点的值
//否则,说明已经满足要求,直接返回即可
//一直往下比较,直到比较到最后一行
size_t parent = start_loc;
size_t child = parent*2 + 1;
while(1)
{
//parent节点最多交换到树的最后一层,则停止交换,此时,child一定大于或等于size
if(child >= heap->size)
{
//说明parent已交换到最后一层
break;
}
//如果右节点存在,在大跟堆中,找左右节点的最大值,小跟堆找左右节点的最小值
//如果是大跟堆,如果左节点元素小于右节点元素
if(child + 1 < heap->size && heap->cmp(heap->data[child],heap->data[child + 1]) == 0)
{
//此时取右节点元素与根节点元素进行比较
child = child + 1;
}
//大跟堆将根节点与孩子节点的最大值进行比较,小跟堆将根节点与左右孩子节点的最小值进行比较
//如果是大跟堆,如果根节点比孩子节点的最大值小,就进行交换
if(heap->cmp(heap->data[parent],heap->data[child]) == 0)
{
//交换
Swap(&heap->data[parent],&heap->data[child]);
//然后更新parent与child的值,继续比较下沉
parent = child;
child = parent*2 + 1;
}
else
{
//此时满足了比较条件,直接返回即可
break;
}
}
return;
}
在下沉式调整函数中,每次都要乘2遍历到下一层,所以时间复杂度也为:log2(n)。因此删除堆顶元素的时间复杂度也为:log2(n)。
5. 根据一个堆来对数组进行排序
(1)首先根据数组元素创建一个堆。如果需要升序则创建大堆,如果是降序则创建小堆。以大堆为例。
(2)大堆创建完成之后,数组中的元素在堆中就满足:根节点必然比左右孩子值大。
(3)然后根据上述的删除函数对堆顶元素进行删除。第一次删除过后,最大的堆顶元素位于存放堆的数组的最后一个位置,第二次删除过后,次大的堆顶元素位于存放堆的数组的倒数第二个位置,...待堆中所有元素删除完之后,存放堆的数组中的元素已按由小到大的顺序排好。(注意:在对堆顶元素进行删除时,是将堆顶元素与数组堆尾元素进行交换,然后size--。虽然说是删除,实际上只是将该内存中的元素视为无效元素,但原堆顶元素依然存放在其中,所以依然可以使用)。
(4)最后,再将存放堆的数组元素依次赋值给已知的数组即可。
代码如下:
//根据堆对数组进行排序,sort_flag等于1表示进行升序排序,等于0表示进行降序排序
//时间复杂度为:nlogn
void HeapSort(HeapType array[],size_t size,int sort_flag)
{
if(array == NULL || size == 0)
{
//非法输入
return;
}
//先根据数组元素创建一个堆
//如果需要升序排序,就创建一个大堆,如果需要降序排序,就需要一个小堆
//堆创建好之后,对堆中元素进行逐个删除
//删除完之后,将堆中元素赋值给数组元素
//此时,数组元素就已经排好序了
//这里对数组进行降序排序
//创建一个堆
Heap heap;
if(sort_flag == 1)
{
HeapInit(&heap,Greater);
}
else
{
HeapInit(&heap,Less);
}
//根据数组元素对堆进行插入元素来创建堆
size_t cur = 0;
for(;cur < size;cur++)
{
HeapInsert(&heap,array[cur]);
}
//依次删除堆顶元素
for(cur = 0;cur < size;++cur)
{
HeapErase(&heap);
}
//删除完成之后,堆中的元素已排好序,将排好序的堆元素在赋值给数组元素
memcpy(array,heap.data,size*sizeof(HeapType));
}
因为上述的插入和删除函数时间复杂度均为:log2(n),且这两个函数都嵌套在一个循环中,所以上述函数的时间复杂度为:nlog2(n)。
6. 清空堆
清空堆时,只需将堆中的所有元素删除,即将size置为0,此时堆中所有元素都为无效元素,既达到了清空的目的。
代码如下:
void HeapEmpty(Heap* heap)
{
if(heap == NULL)
{
//非法输入
return;
}
heap->size = 0;
return;
}
7. 销毁堆
销毁堆时,不仅要将堆中所有元素清空,还需将表示大小堆的函数指针置空。
//销毁堆
int HeapDestroy(Heap* heap)
{
if(heap == NULL)
{
//堆已销毁
return 0;
}
heap->size = 0;
heap->cmp = NULL;
return 1;
}
8. 统计堆中结点个数
存放堆的数组实际元素个数size即为堆中的结点个数。
//统计堆中元素个数
size_t HeapSize(Heap* heap)
{
if(heap == NULL)
{
//非法输入
return (size_t)-1;
}
return heap->size;
}