高数压轴题思路和一些未掌握内容（最近更新：2020/1/10）

---

0 写在前面

持续更新中，作者为2021年考研，目标NJU，写这篇文章的目标是提供压轴题思路，而对于基础题则可以参考《闭关修炼》，有任何意见都可以私信我。
2019/11/22更新：文章做了比较大的改版，目前该文章有些杂乱，原因是目前在第一阶段打基础，对于自己薄弱的部分还需要用题来巩固，在不久的之后，未掌握内容会逐渐减少，压轴题（难题）部分内容会逐渐增加。
2020/1/10更新：持续学习中…
参考资料：

1. 张宇《高等数学18讲（2017年）》
2. 张宇《考研数学闭关修炼》
3. 陈兆东等《大学生数学竞赛习题精讲（第2版）》
4. 张天德等《全国大学生数学竞赛辅导指南（第2版）》

1 未掌握内容

• 高阶导数求法（泰勒公式、归纳法、莱布尼兹公式）

5. 曲率和曲率半径

• 曲线 $L:y=f(x)$，曲率 $\displaystyle K=\frac{|y''|}{(1+y'^2)^{\frac{3}{2}}}$；
• 曲线 $L:x=\phi(t),y=\Phi(t)$，曲率 $\displaystyle K=\frac{|\phi'\Phi''-\phi''\Phi'|}{(\phi'^2+\Phi'^2)^\frac{3}{2}}$
• 曲率半径 $R=\frac{1}{K}$

1. 多元极限存在（略）
2. 多元函数连续（略）
3. 偏导数存在（一动一静，略）
4. 全微分存在（全微分存在）
   $\Delta z=f_x'\Delta x+f_y'\Delta y+O(\rho),\rho=\sqrt{(\Delta x)^2+(\Delta y)^2}$
5. 偏导数连续

$5\to4\to2\to1$
$4\to3$

• 雅可比式
  $J=\frac{\partial(F,G)}{\partial(u,v)}=|\frac{\partial F}{\partial u}, \frac{\partial F}{\partial v};\frac{\partial G}{\partial u} ,\frac{\partial G}{\partial v}|$

1. 方向导数
   若 $f(x,y,z)$在 $P(x,y,z)$点处可微，则函数在P点沿着 ${\bf l}=(\cos\alpha,\cos\beta,\cos\gamma)$的方向导数为 $\frac{\partial f}{\partial {\bf l}}=f_x\cos\alpha+f_y\cos\beta+f_z\cos\gamma$
2. 梯度
   $grad f(x,y)=(f_x,f_y)$
3. 散度和旋度
   设 $A(x,y,z)=(P(x,y,z),Q(x,y,z),R(x,y,z))$
   则散度 $divA=\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}+\frac{\partial R}{\partial z}$，旋度为 $rotA=|i ,j ,k;\frac{\partial }{\partial x},\frac{\partial }{\partial y},\frac{\partial }{\partial z};P,Q,R|$

• 区间再现公式
  
• 华里士公式
  
  
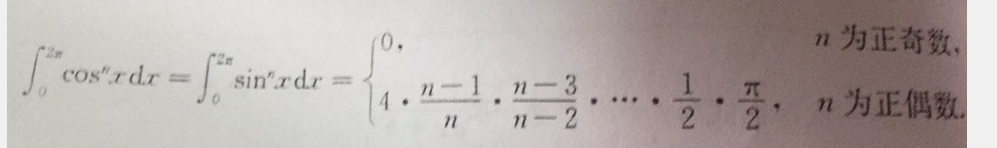
  n为偶数： $I_n=\int_0^{\frac{\pi}{2}}\sin^n xdx=\int_0^{\frac{\pi}{2}}\cos^n xdx=\frac{\pi}{2}\cdot \frac{(n-1)!!}{(n)!!}$
  n为大于1的奇数： $I_n=\int_0^{\frac{\pi}{2}}\sin^n xdx=\int_0^{\frac{\pi}{2}}\cos^n xdx= \frac{(n-1)!!}{(n)!!}$

9. 特殊的广义积分

• 伽马函数 $\Gamma(s)=\int_0^{+\infty}x^{s-1}e^{-x}dx(s>0)$， $\Gamma(s+1)=s\Gamma(s)$
• 高斯积分 $\int_{-\infty}^{+\infty}e^{-x^2}dx=\sqrt{\pi}$

10. 特殊积分
    
12. 积分为区间长度的一半
13. 正交的积分

• 平移换系
  令 $u=f(x,y),v=g(x,y)$，则 $dxdy=|J|dudv$，其中 $J=|x_u,x_v;y_u,y_v|$

• 球面坐标系（ $r^2\sin \psi drd \psi d \theta$）
  $x=r\sin\psi \cos\theta,y=r\sin\psi \sin\theta,z=r\cos\psi$

3. 转动惯量
   对于平面薄片，面密度为 $\rho(x,y)$，D是薄片所占的平面区域，则薄片对x轴、y轴和原点O的转动惯量分别为 $I_x=\iint_Dy^2\rho(x,y)d\sigma,I_y=\iint_Dx^2\rho(x,y)d\sigma,I_O=\iint_D(x^2+y^2)\rho(x,y)d\sigma.$
   空间物体、光滑曲线、光滑曲面的转动惯量可以类推。
4. 引力
   对于平面薄片，它对点 $M_0(x_0,y_0,z_0)$处的质量为m的质点的引力 $(F_x,F_y,F_z)$为
   $F_x=Gm\iint_D\frac{\rho(x,y)(x-x_0)}{[(x-x_0)^2+(y-y_0)^2+(z-z_0)^2]^{\frac{3}{2}}}d\sigma$
   $F_y=Gm\iint_D\frac{\rho(x,y)(y-y_0)}{[(x-x_0)^2+(y-y_0)^2+(z-z_0)^2]^{\frac{3}{2}}}d\sigma$
   $F_z=Gm\iint_D\frac{\rho(x,y)(z-z_0)}{[(x-x_0)^2+(y-y_0)^2+(z-z_0)^2]^{\frac{3}{2}}}d\sigma$
   其中 $G$为引力系数。空间物体、光滑曲线、光滑曲面的引力可以类推。

3.3 曲线曲面积分

3.3.1 曲线积分

3.3.1.1 第一型

第一型曲线积分中的f可以理解为曲线的密度。

计算方法有：

1. 基本性质（略）
2. 化为定积分
   参数方程 $x=x(t),y=y(t)$（ $ds=\sqrt{x'^2+y'^2}dt$），直角坐标系方程 $y=y(x)$（ $ds=\sqrt{1+y'^2}dx$），极坐标系方程（ $ds=\sqrt{r^2+r'^2}d\theta$）。（三维空间略）
3. 形心公式的逆用（略）

3.3.1.2 平面第二型

第二型曲线积分中的f依然是曲线的密度，不过该曲线是带方向的。

$\int_CP(x,y)dx+Q(x,y)dy$
计算方法有：

1. 基本性质（略）
2. 两型曲线积分的转换（如何表示方向：( $\cos\alpha,\cos\beta,\cos\gamma$)）
3. 化为定积分
   参数方程 $x=x(t),y=y(t)$（dx=x’dt,dy=y’dt），直角坐标系类似第一型，这里不再赘述。
4. 格林公式
   若D是以光滑正向（正向即逆时针）闭曲线C为边界的平面区域，则 $\int_CPdx+Qdy=\iint_D(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y})d\sigma$
   构造格林公式的方法（添线法（构造椭圆或圆或垂线））
5. 四个等价条件（略，基本上就是说如果曲线积分与路线无关，只与起点和终点有关，则闭曲线积分为0）
6. 凑微分法

3.3.1.3 空间第二型

$\int_lP(x,y,z)dx+Q(x,y,z)dy+R(x,y,z)dz$
斯托克斯公式
对于光滑曲面 $\Sigma$的边界闭曲线 $l$，若 $l 和\Sigma$同向（同正或同负），则
$\int_lP(x,y,z)dx+Q(x,y,z)dy+R(x,y,z)dz=$

$\iint_\Sigma(\frac{\partial R}{\partial y}-\frac{\partial Q}{\partial z})dydz+(\frac{\partial P}{\partial z}-\frac{\partial R}{\partial x})dxdz+(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y})dxdy=$

$\iint_\Sigma|dydz,dzdx,dxdy;\frac{\partial }{\partial x},\frac{\partial }{\partial y},\frac{\partial }{\partial z};P,Q,R|$

3.3.2 曲面积分

3.3.2.1 第一型

第一型曲面积分中的f可以理解为曲面的密度。

$\iint_\Sigma P(x,y,z)dydz+Q(x,y,z)dxdz+R(x,y,z)dxdy$
计算方法有：

1. 基本性质（略）
2. 化为二重积分
   直角坐标系方程 $z=z(x,y)$（ $dS=\sqrt{1+z_x^2+z_y^2}dxdy$）（注意投影不能重合，即 $z=z(x,y)$为单值函数）。
3. 形心公式的逆用（略）

3.3.2.2 第二型

第二型曲面积分中的f依然是曲面的密度，不过该曲面是带方向的。

计算方法有

1. 基本性质（略）
2. 化为二重积分
   将原函数分为三部分分别投影到对应的坐标面上，以 $\iint_\Sigma R(x,y,z)dxdy$为例，首先得到不能重合的 $xOy$面上的投影 $D_{xy}$，则 $\iint_\Sigma R(x,y,z)dxdy=\pm \iint_{D_{xy}}R(x,y,z(x,y))dxdy,$注意这里的 $\pm$为曲面的方向，若为上、右、前侧（曲面的法向量与z正轴的夹角为锐角时）则为 $+$，否则为 $-$。
3. 两型曲面积分的转换，同曲线积分的转换方法。
4. 高斯公式
   与格林公式类似 $\Sigma$为闭曲面，围住的区域为 $\Omega$，则
   $\iint _ \Sigma Pdydz+Qdzdx+Rdxdy=\iiint_\Omega (\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}+\frac{\partial R}{\partial z})dv$
   构造高斯公式的方法（补面法）

3.3.3 题型讲解

不等式证明

（1） $2|ab|\le a^2+b^2;|a\pm b|\le|a|+|b|;||a|-|b||\le |a-b|$；
（2） $|a_1\pm a_2\pm ...\pm a_n|\le |a_1|+|a_2|+...+|a_n|;|\int^b_af(x)dx|\le \int_a^b|f(x)|dx$是（1）的推广；
（3）设 $a_1,a_2,...,a_n>0$，则 $\frac{a_1+a_2+...+a_n}{n}\ge \sqrt[n]{a_1a_2...a_n};|\frac{a_1+a_2+...+a_n}{n}|\le \sqrt{\frac{a_1^2+a_2^2+...+a_n^2}{n}}$，等号成立为a相等；
（4） $x,y,p,q>0$，若 $\frac{1}{p}+\frac{1}{q}=1$，则 $xy\le \frac{x^p}{p}+\frac{x^q}{q}$
5. 柯西-施瓦兹不等式，乘积的次方≤次方的乘积

• $(a^2+b^2)(c^2+d^2)\ge (ac+bd)^2$
• $[\int_a^bf(x)g(x)dx]^2\le \int^b_af^2(x)dx\cdot \int_a^bg^2(x)dx$
  
  
  （7） $|\int_a^bf(x)g(x)dx|\le [\int^b_a|f(x)|^pdx]^{\frac{1}{p}}\cdot [\int_a^b|g(x)|^qdx]^{\frac{1}{q}},p>1,\frac{1}{p}+\frac{1}{q}=1$是（6）的一般式
  （8）放缩法（略）
  （9）伯努利不等式： $(1+x)^\alpha \ge1+\alpha x$
  （10）若尔当不等式： $\frac{2\theta}{\pi}\le\sin\theta\le\theta$
  （11）
  （12）
  

5.3 傅里叶级数

傅里叶级数f(x0+)+f(x0-)/2
迪利克雷定理
题型讲解

六、微分方程

6.1 一阶微分方程

4. 伯努利 $y'+P(x)y=Q(x)y^\alpha$
   两边同除以 $y^\alpha$，凑微分，令 $z=y^{1-\alpha}$可得 $z'+(1-\alpha)P(x)z=(1-\alpha)Q(x)$，转为3
5. 全微分方程

6.3.2 非齐次特解的解法

解的结构：齐次的解+特解，若右端项为 $q(x)$则有以下解法

1. 18讲中的待定系数法
2. 算子解法
   算子即 $D=\frac{d}{dx}$，则特解可以表示为 $y=\frac{1}{f(D)}q(x)$
   当 $q(x)$为n次多项式时，将 $\frac{1}{f(D)}$利用多项式除法（泰勒级数展开）到n次项为止。

6.4 欧拉方程

七、解析几何（略）

$\vec{l_1}=(a_1,b_1,c_1)$， $\vec{l_2}=(a_2,b_2,c_2)$， $p_1=(x_1,y_1,z_1)$， $p_2=(x_2,y_2,z_2)$

1. 两直线的距离公式
   $d=\frac{\vec{p_1p_2}\cdot(\vec{l_1}\times \vec{l_2})}{|\vec{l_1}\times \vec{l_2}|}$
2. 经过直线的平面,平面束方程

2 压轴题记录

证明题

遇到极限和导数可以考虑导数定义
泰勒公式：遇到高阶导数或者是需要得到一个特殊的数值

4.5.1 中值等式问题

4.5.1.1 单中值问题（ $\xi$）

（1）将中值等式中的 $\xi$换成x，令y=f(x)；
（2）解微分方程，把通解表达为G(x,y)=C的形式；
（3）得到辅助函数 $F(x)=G(x,f(x))$；
（4）利用罗尔定理得出结论。
例1：

4.5.1.2 多中值问题

这种题的难点在于找到分割点，常用拉格朗日中值定理和柯西中值定理

3 超纲备用知识

• Stolz定理（离散的洛必达公式）
  设数列 $\{b_n\}$单调增加且 $\displaystyle \lim_{n\to \infty}b_n=+\infty$，若右端存在或为无穷则 $\displaystyle \lim_{n\to \infty}\frac{a_n}{b_n}=\lim_{n\to \infty}\frac{a_n-a_{n-1}}{b_n-b_{n-1}}$