我用程序求解2020广东高考理数压轴题

Python求解2020广东高考理科数学第21题

先看看原题长啥样

已知 $f(x) = e^x + ax^2 - x$
(1)当 $a=1$ 时，论 $f(x)$ 单调性
(2)当 $x \geq 0$ 时， $f(x) \geq \frac{1}{2} x^3 + 1$ ，求a取值范围

第1问论单调性就是求导，一次不行就来多一次；我们来重点看看第2问

对于 $e^x + ax^2 - x \geq \frac{1}{2}x^3 + 1$

$x=0$ 时， $a \in R$

$x>0$ 时，把 $a$ 放一边，转成：
$a \geq \frac{\frac{1}{2}x^3 +1 + x - e^x}{x^2}$

然后我们构造 $g(x)$
$g(x) = \frac{\frac{1}{2}x^3 +1 + x - e^x}{x^2}$
接下来就是求解 $g(x)$ 的最大值

那么问题来了，函数有点丑，最值不好求。

咱们先用程序把函数构造出来

def g(x):
    """广东高考理数第21题第2问目标函数"""
    return ((1/2)*(x**3) + x + 1 - np.exp(x)) / (x**2)

然后暴力循环，x取 $(0,100000]$

max(g(np.linspace(100000, 0, 99999, False)))

虽然可以快速求出一个值-0.09726402479239056，但显然精度不够

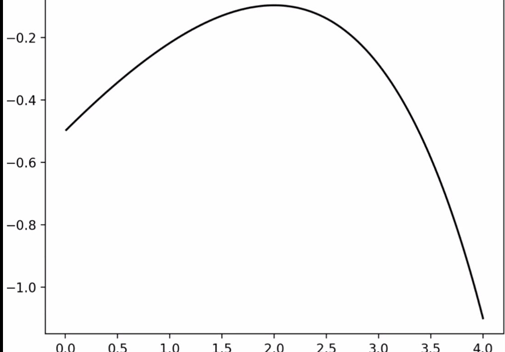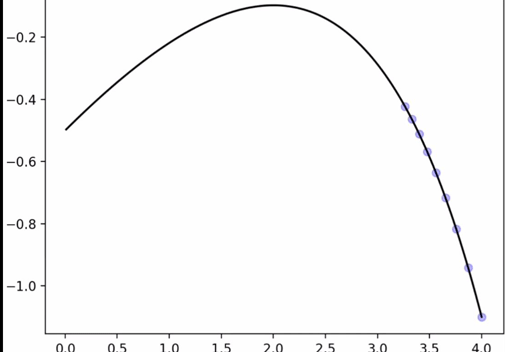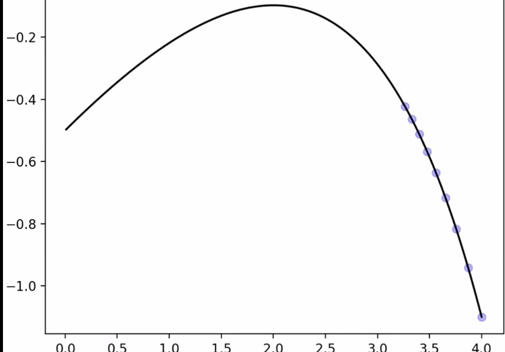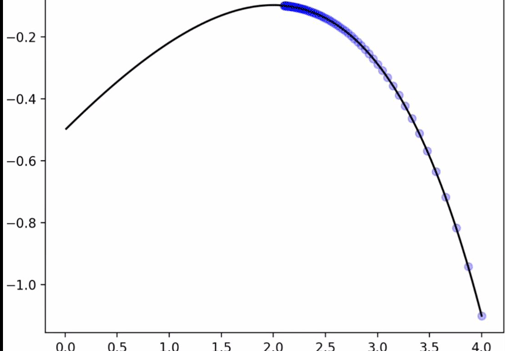
画个图看看

mp.plot(X, g(X), c='black')

$x \in (0,10]$ 时，肉眼可见x越大g(x)越小
$x \in (0,4]$ 时，肉眼可见 $x=2$ 处函数取最大值 $\frac{7-e^2}{4}$

print((7-np.exp(2))/4)

$a \in [-0.0972640247326626,+\infty)$

然而眼见未为实，万一瞎眼识渣女？

据上图示，函数先增后减，有一个极大值，这个极大值就是最大值，我们可以借助程序求出这个极值点，然后得出极大值。

delta = 0.000000001

def derivative(Xi):
    """求f'(Xi)"""
    return (g(Xi + delta) - g(Xi)) / delta

如何判断 $x_i$ 是否极值点？我们可以求 $x=x_i$ 处导数

$g'(x_i) = \frac{g(x_i+\Delta x)-g(x_i)}{\Delta x}$

求出 $g'(x_i)$ 后，我们可以根据 $g'(x_i)$ 的值来更新 $x_i$
当 $g'(x_i)>0$ 时， $x_i$ 往大于零的方向走一步，逼近极值点
当 $g'(x_i)<0$ 时， $x_i$ 往小于零的方向走一步，逼近极值点
$g'(x_i)$ 绝对值越大， $x_i$ 每次走的步伐也就越大

就像爬山一样，经过不断迭代，一步步逼近极值点

我妹做的GIF
精度为0.00000001时，算出极值点2.0000003896307703，最大值-0.09726402473268528

梯度上升完整代码

import matplotlib.pyplot as mp, numpy as np

# Δx
delta = 1e-9
# 步长，即学习速率
alpha = 0.1
# 允许误差范围
precision = delta / alpha
# 区间
X = np.linspace(4, 0, 400, False)


def g(x):
    """广东高考理数第21题第2问目标函数"""
    return ((1/2)*(x**3) + x + 1 - np.exp(x)) / (x**2)


def derivative(Xi):
    """求g'(Xi)"""
    return (g(Xi + delta) - g(Xi)) / delta


# 绘制函数曲线
mp.plot(X, g(X), c='black')
# 初始化极值点
extreme_point = np.random.choice([.1, 4])
# 初始化误差
error = np.inf
# 迭代（误差小于精度时退出）
while abs(error) >= precision:
    # 绘制当前极值点
    mp.scatter(extreme_point, g(extreme_point), c='b', alpha=.3)
    # 迭代步伐
    error = alpha * derivative(extreme_point)
    # 更新极值点
    extreme_point = extreme_point + error
    # 动态展示
    print(extreme_point, error)
    mp.pause(abs(error))
# 极值点代入函数，求得极大值
maximum = g(extreme_point)
print('g(x)max =', maximum)

print: g(x)max = -0.09726402473268528

求任意函数最大值完整代码

import numpy as np

# Δx
delta = 1e-9
# 步长，即学习速率
alpha = 0.1
# 允许误差范围
precision = delta / alpha


def get_max_point(f, x):
    """获取f(x)最大时的x"""
    return max((f(xi), xi) for xi in x)[1]


def derivative(xi, f):
    """求f'(Xi)"""
    return (f(xi + delta) - f(xi)) / delta


def maximum_solution(f, x=np.linspace(99999, 0, 999999, False)):
    """求任意函数最大值"""
    # 初始化极值点
    extreme_point = get_max_point(f, x)
    # 初始化误差
    error = np.inf
    # 迭代（误差小于精度时退出）
    while abs(error) >= precision:
        # 迭代步伐
        error = alpha * derivative(extreme_point, f)
        # 更新极值点
        extreme_point = extreme_point + error
    # 极值点代入函数，求得极大值
    maximum = g(extreme_point)
    return extreme_point, maximum


def g(x):
    """广东高考理数第21题第2问目标函数"""
    return ((1/2)*(x**3) + x + 1 - np.exp(x)) / (x**2)


print(maximum_solution(g))

print: (1.9999989031249044, -0.0972640247328422)