强化学习：基于模型的动态规划

1、最优价值函数

最优状态价值函数： 考虑到这个状态下，可能发生的所有后续动作，并且都挑最好的动作来执行的情况下，这个状态的价值。

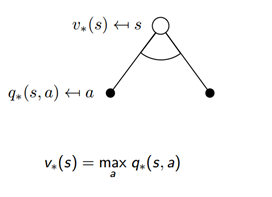
最优状态动作值函数： 在这个状态下执行了一个特定的动作，然后考虑到执行这个动作后有可能处于的后续状态并且在这些状态下总是选取最好的动作来执行所得到的长期价值。

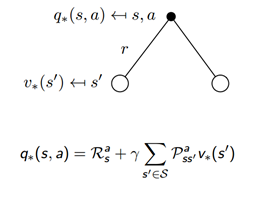
Bellman方程：

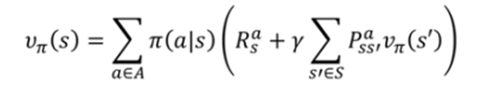
忽略策略的随机性，Bellman方程可以写作：

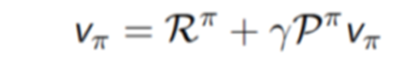
使用矩阵直接求解，则有：

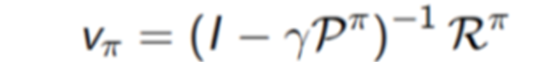
Bellman方程的复杂度为 $O({n^3})$,在真实场景中P和R的规模都很大，无法直接求解出来。

2、动态规划方法

  动态规划的思想就是把复杂的问题分阶段进行简化，逐步简化成简单的问题。“动态”指的是该问题的时间序列部分，“规划”指的是去优化一个计划，即，优化一个策略。动态规划问题的求解需要迭代进行，比如下面的例子，计算台阶的走法：

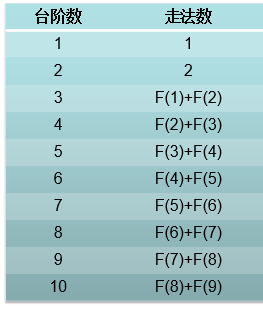
  当只有1级台阶和两级台阶的时候，分别是1种和2种走法，迭代进行时，每一次迭代过程中，只要保留之前的两个状态，就可以推导出新的状态。不需要像备忘录那样保留全部的子状态，就实现了时间和空间上的最优化。
使用动态规划求解问题需要满足的条件：
最优子结构：保证能够使用最优性准则，从而问题的最优解可以分解为子问题最优解；
重叠子问题：子问题重复出现多次，因而可以缓存并重用子问题的解。在MDP中，贝尔曼方程给出了问题的迭代分解，值函数保存和重用问题的解。
动态规划的步骤：
a)将问题分解为子问题；
b)求解子问题；
c)合并子问题的解。
最优子结构： 最优子结构是依赖特定问题和子问题的分割方式而成立的条件。各子问题具有最优解，就能求出整个问题的最优解，此时条件成立。如果不能利用子问题的最优解获得整个问题的最优解，那么这种问题就不是最优子结构。
  可以利用动态规划求解MDP问题，此时MDP的模型是已知的。动态规划方法既可用于预测问题，也可以用于控制问题。
预测问题： 输入：MDP<S, A, P, R, γ>，输出：值函数 ${v_\pi }$
控制问题： 输入：MDP<S, A, P, R, γ>，输出：最优值函数 ${v_*}$和最优策略 $\pi_*$

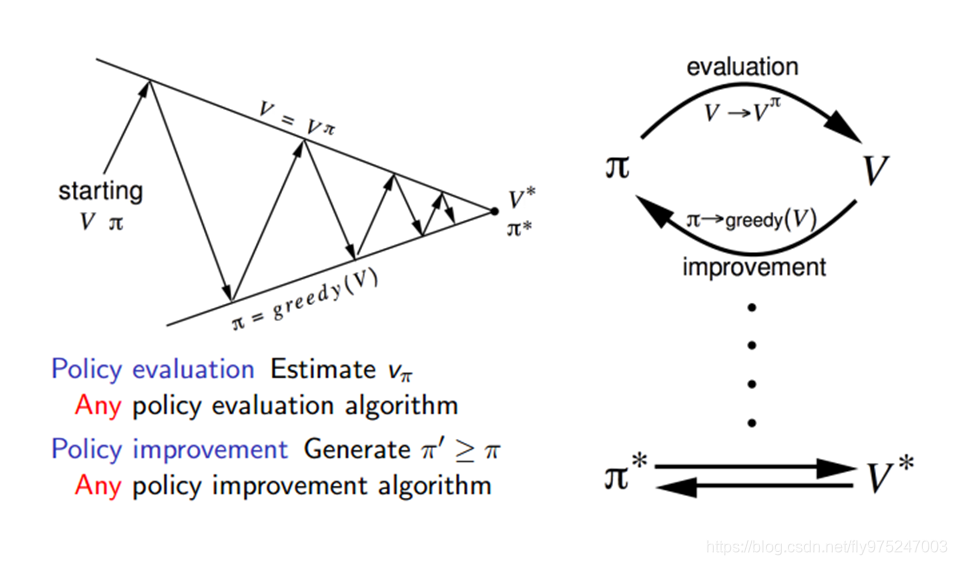
2.1、策略迭代

  策略迭代算法通过构建值函数（而不是最优函数）来评估，然后利用这些值函数，寻找新的，改进的策略。迭代应用Bellman期望方程，在每次迭代过程中对于第k+1次迭代，所有的状态s的价值都用 $v_k(s&#x27;)$计算，并更新该状态第k+1次迭代中所使用的价值 $v_k(s)$,其中s’是s的后继状态。通过反复迭代最终收敛至 $v_\pi$
${v_{k + 1}}(s) = \sum\limits_{a \in A} {\pi (a|s)(R_s^a + \gamma \sum\limits_{{s&#x27;} \in S} {P_{s{s&#x27;}}^a{v_k}(s&#x27;)} )}$
迭代示例—格子世界：

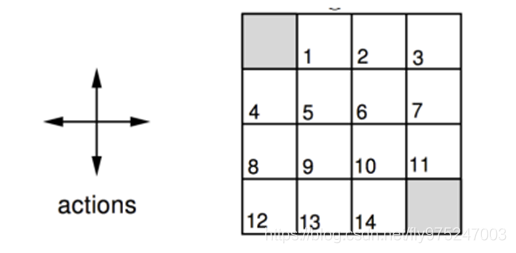
状态空间为S={1,2,3,4,…,14}，为非终止状态，灰色方格为终止状态。动作空间A={东，南， 西， 北}，回报函数r=-1，需要评估的策略为随机策略。

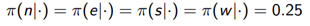
迭代过程：

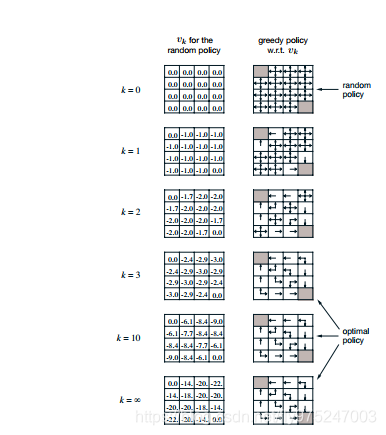
通过格子世界的示例，得到了一个优化策略的方法，分为两步：
给定一个策略π
1）迭代更新价值函数：

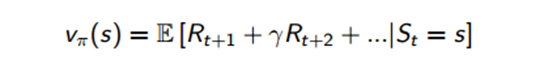
2）之后在当前策略的基础上，贪婪地选取行为，使得后继状态价值增加最多：

在小格子世界中，改进的策略是最优的，π’=π*，一般需要许多次迭代才能找到最优策略，策略迭代过程一般总是收敛到π*
策略迭代分两步走：
第一步：先任意假设一个策略 $\pi_k$，使用这个策略迭代价值函数直到收敛（策略评估）

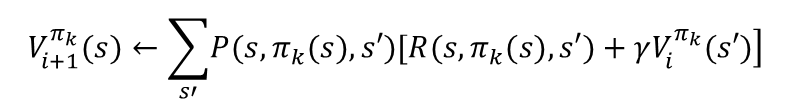
最后得到的V(s)就是使用策略 $\pi_k$，能巩固取得的最好价值函数V(s)。
第二步：重新审视每个状态所有可能的行动Action，优化策略 $\pi_k$，看看有没有更好的Action可以代替老的Action：

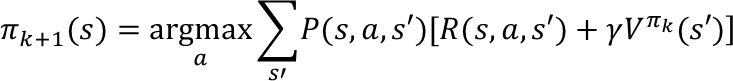
策略迭代最后得到了每个状态应有的最佳策略。

策略迭代的伪代码：

2.2、值迭代

最优状态值函数： 最优状态值函数 $v_*(s)$是在从所有策略产生的状态价值函数中，选取使状态s价值最大的函数： ${v_*}(s) = \mathop {\max }\limits_\pi v_\pi(s)$**最优状态行为值函数：**最优状态行为值函数 $q_*(s,a)$是从所有策略产生的行为价值函数中选取使状态行为对<s, a>价值最大的函数： ${q_*}(s,a) = \mathop {\max }\limits_\pi q_\pi(s, a)$Bellman最优公式：
1）最优状态值函数：

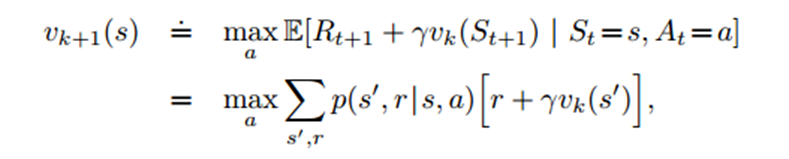
2）最优状态行为值函数：

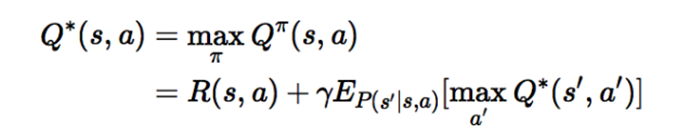
价值迭代： 先更新每个状态s的长期价值V(s)，这个价值是立即回报R(s,a)与下一个状态s+1的长期价值的综合，从而获得更新。每次迭代，对于每个状态s，都要更新价值寒素V(s)。对于每个状态s的价值更新，需要考虑所有行动Action的可能性。（跟采用什么样的策略已经没有关系了）

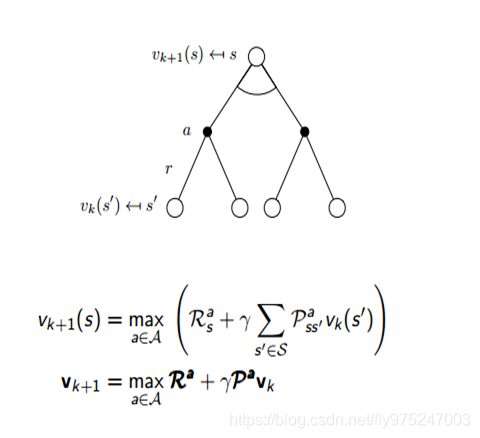
价值迭代的伪代码：

伪代码说明：

Initialization：初始化所有状态的v(s)
Finding optimal value function（寻找最优的价值函数）：
	对每一个当前状态s，对每个可能的动作a，都计算一下采取这个动作后达到的下一个状态的期望价值。
	看哪个动作可以到达的状态的期望价值最大，就将这个最大期望价值函数作为当前状态的价值函数v(s)
	循环执行这个步骤，直到价值函数收敛，就可以得到最优optimal的价值函数了
Policy extraction:利用上面步骤得到的optimal价值函数和状态转移概率，就计算出每个状态应该采取的optimal动作，这个是deterministic。

2.2.1、值迭代示例

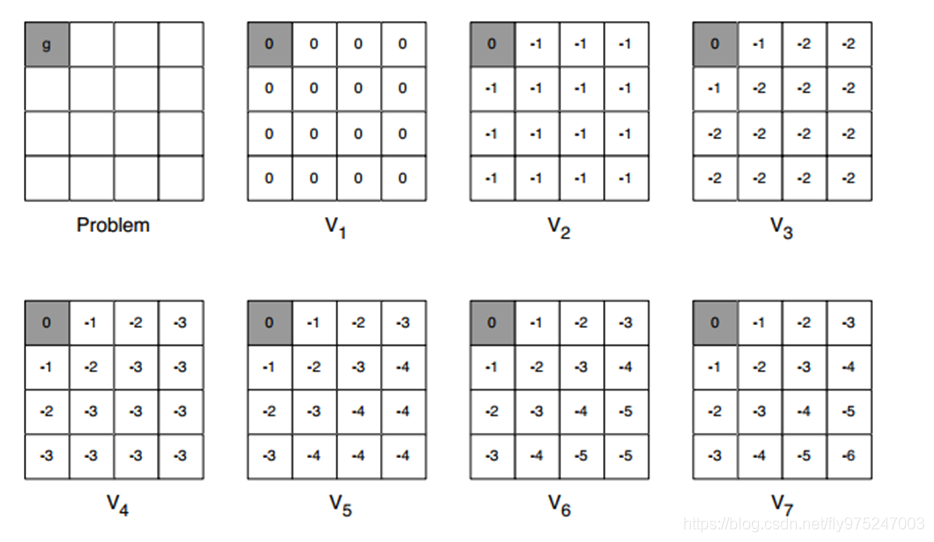
格子世界：除了终点（灰色格子）的reward=0，其他的状态reward=-1。
在迭代过程中，距离g最近的两个格子（A和D）的V(s)最先可以算出最大值。

  对于A，只要选择向左，就可以达到终点获得reward。而向右则没有奖赏。根据公式中的max，A就会选择左走，它的V值最大，所以第一次迭代它就已经可以获得最大值。对于B，第一次迭代向左和向右都一样，第二次迭代中，两次向左可以达到最大值。

2.3、策略迭代和值迭代的异同

Policy iteration: 使用bellman方程来更新value，最后收敛的value即 $v^\pi$是当前policy下的value值（所以叫做对policy进行评估），目的是为了后面的policy improvement得到新的policy。
Value iteration: 使用bellman最优方程来更新value，最后收敛得到的value即 $v^*$就是当前状态下的最优的value值。因此，只要最后收敛，那么最优的policy也就得到。
  策略迭代的第二步policy evaluation与值迭代的第二步finding optimal value function十分相似，除了后者用了max操作，前者没有max。因此后者可以得出optimal value function，而前者不能得到optimal function。
  策略迭代的收敛速度更快一些。在状态空间较小时，最好选用策略迭代方法；当状态空间较大时，值迭代的计算量更小一点本质上依赖于模型，而且理想条件下需要遍历所有的的状态，在稍微复杂一点的问题上基本不可能。

关于示例程序，下回分解。