欧拉降幂
公式:
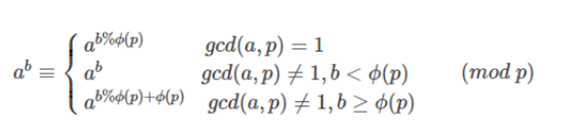
例题:
poweroj - 2366
题目描述:
题意:计算ab的c次幂 %1000000007。
输入:a,b,c。
输出:取模后的结果。
分析:
这道题就是一个板子,直接套公式,只不过有两层。直接完全套公式…很暴力。
代码:
#include<stdio.h>
#include<iostream>
#include<algorithm>
#include<string>
#include<cstring>
#include<cmath>
#include<stack>
using namespace std;
#define maxn 100005
typedef long long ll;
const int p=1e9+7;
ll qsm(ll a,ll b,ll p){
ll res=1;
res%=p;
while(b){
if(b&1) res=res*a%p;
a=(a*a)%p;
b>>=1;
}
return res;
}
ll ph(ll n){
ll ans=n;
for(int i=2;i*i<=n;i++){
if(n%i==0){
ans=ans*(i-1)/i;
while(n%i==0) n/=i;
}
}
if(ans>1) ans=ans*(n-1)/n;
return ans;
}
ll gcd(ll a,ll b){
return b==0?a:gcd(b,a%b);
}
int main(){
ll a,b,c,d;
while(scanf("%lld%lld%lld",&a,&b,&c)!=EOF){
ll mi=ph(p-1);
if(gcd(b,p-1)!=1){
if(c>=mi) c=(c%mi)+mi;
}
else c=c%mi;
d=qsm(b,c,p-1);
printf("%lld\n",qsm(a,d%(p-1),p));
}
return 0;
}
卢卡斯定理:
引言:
这里我们先引入组合数的概念,即从n个不同元素中,任取m(m≤n)个元素并成一组,叫做从n个不同元素中取出m个元素的一个组合;从n个不同元素中取出m(m≤n)个元素的所有组合的个数,叫做从n个不同元素中取出m个元素的组合数。

这里的两条性质十分重要,要牢记,来一个组合数的模板题目。
题目:SWUST OJ 82
题目描述
编写一个函数,求从n 个不同的数中取r 个数的所有选择的个数。
输入
输入n 和r 的值; 当用户输入0 0 时,程序结束。
输出
根据公式: C(n,r) = C(n, r-1) * (n - r + 1) / r 输出运算结果 输入数据不满足题意时候,输出"error!"
样例输入
复制
5 3
10 20
50 3
0 0
样例输出
10
error!
19600
说明:
他给出的这个公式也是对的,但是我感觉这道题没必要,但是其实这个公式很强,可以这样写
double c(int n, int m) {
double res = 1;
for(int i=1;i<=m;i++) {
res = res*(n-i+1)/i;
}
return res;
}
你以为完了吗,不,还有一种求法,用矩阵来求:
double a[maxn][maxn];
void c(){
a[0][0]=1.0;
for(int i=1;i<maxn;i++){
for(int j=0;j<=i;j++){
if(j==0||j==i) a[i][j]=1;
else a[i][j]=a[i-1][j-1]+a[i-1][j];
}
}
}
这里我为什么用double呢,因为有道题就是这样卡了我很久。
代码:
这里面有我第3种组合数求法,但是对于大的数据,这种最容易超时。
#include<iostream>
#include<stdio.h>
#include<cstring>
#include<algorithm>
#include<math.h>
#include<vector>
using namespace std;
typedef long long ll;
const int maxn=1e5+5;
const int inf=0x3f3f3f3f;
int c(int n,int m){
if(m==0||n==m) return 1;
if(n>m) return c(n-1,m)+c(n-1,m-1);
}
int main(){
int n,m;
while(~scanf("%d%d",&n,&m)){
if(n==0&&m==0) return 0;
if(n<m) cout<<"error!"<<endl;
else cout<<c(n,m)<<endl;
}
return 0;
}
卢卡斯:
其实没什么了就是一个公式,做题的时候再套一下上面组合数的板子就ok了。


言归正传:
那么现在,now,我们就来给出一道卢卡斯的模板题。
题目:
模板题:洛谷 P3807
题目背景
这是一道模板题。
题目描述
给定n,m,p(1≤n,m,p≤10 ^5)
求c(m,m+n)%p。
保证P为prime
C表示组合数。
一个测试点内包含多组数据。
输入格式
第一行一个整数T(T\le 10T≤10),表示数据组数
第二行开始共T行,每行三个数n m p,意义如上
输出格式
共T行,每行一个整数表示答案。
输入输出样例
输入 #1
2
1 2 5
2 1 5
输出 #1
3
3
思考:
卢卡斯模板题,但是在做卢卡斯的时候要回忆一下快速幂和欧拉定理,为什么呢,因为里面涉及到了除法,除法可是不能取模的哦。那么因此,我们需要转化为乘法来做。回想一下费马小定理,当p为质数的时候,我们有ap-1%p=1%p,故1/i就可以转化为ip-2%p,这样就能解决除法了呀,满足卢卡斯的条件就是p为质数所以一定成立。另外需要注意的是,对于c(n/p,m/p)其实是一个递归的过程,因此最后写出来的程序如下:
#include<iostream>
#include<stdio.h>
#include<cstring>
#include<algorithm>
#include<math.h>
#include<vector>
using namespace std;
typedef long long ll;
const int maxn=1e6+5;
const int inf=0x3f3f3f3f;
int f[maxn];
ll qsm(ll a,ll b,ll p){
ll res=1;
while(b){
if(b&1) res=(res*a)%p;
b>>=1;
a=(a*a)%p;
}
return res;
}
ll c(ll n,ll m,ll p){
ll res=1;
for(ll i=1;i<=m;i++){
res=res*(n-i+1)*qsm(i,p-2,p)%p;
}
return res%p;
}
ll lucas(ll n,ll m,ll p){
if(m==0||n==m) return 1%p;
return lucas(n/p,m/p,p)%p*c(n%p,m%p,p)%p%p;
}
int main(){
int t;
ll n,m,p;
scanf("%d",&t);
while(t--){
scanf("%lld%lld%lld",&n,&m,&p);
printf("%lld\n",lucas(n+m,m,p));
}
return 0;
}
